4 Types of Tree Traversal Algorithms

Tree traversal is the process of searching a tree data structure one node at a time and performing an operation like checking the node data or updating the node.

In this article, you’ll learn about the theories around such algorithms and how to implement these algorithms through code.

What Is a Tree Data Structure?

Before jumping into the tree traversal algorithms, let’s define a tree as a data structure first. That will help you to grasp the concepts in a meaningful way.

A tree is a hierarchical data structure that stores information in the form of hierarchy, unlike linear data structures like linked list, stack, etc. A tree contains nodes (data) and connections (edges) that don’t form a cycle.

Tree Data Structure Terminology to Know

The following are the few frequently used terminologies for a tree data structure.

• Node: A node is a structure that may contain a value or condition, or represent a separate data structure.
• Root: The top node in a tree, the prime ancestor.
• Child: A node directly connected to another node when moving away from the root, an immediate descendant.
• Parent: The converse notion of a child, an immediate ancestor.
• Leaf: A node with no children.
• Internal node: A node with at least one child.
• Edge: The connection between one node and another.
• Depth: The distance between a node and the root.
• Level: the number of edges between a node and the root + 1
• Height: The number of edges on the longest path between a node and a descendant leaf.
• Breadth: The number of leaves.
• Subtree: A tree T is a tree that consists of a node in T and all of its descendants in T.
• Binary Tree: is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.
• Binary Search Tree: is a special type of binary tree which has the following properties. The left subtree of a node contains only nodes with keys lesser than the node’s key. The right subtree of a node contains only nodes with keys greater than the node’s key. The left and right subtree each must also be a binary search tree.

For the sake of simplicity, we will use a binary tree as an example to understand tree traversal algorithms. But those algorithms can be generalized to other types of tree, as well.

What Is Tree Traversal?

Tree traversal, also known as tree search, is a process of visiting each node of a tree data structure. During tree traversal, you visit each node of a tree exactly once and perform an operation on the nodes like checking the node data (search) or updating the node. 

Tree traversal algorithms can be classified broadly in the following two categories by the order in which the nodes are visited:

• Depth-first search (DFS) algorithm: It starts with the root node and first visits all nodes of one branch as deep as possible before backtracking. It visits all other branches in a similar fashion. There are three subtypes under this that we will cover in this article.
• Breadth-first search (BFS) algorithm: This also starts from the root node and visits all nodes of current depth before moving to the next depth in the tree. We will cover one algorithm of BFS type in the upcoming section.

More on Machine Learning:Random Forest Classifier: A Complete Guide to How It Works in Machine Learning

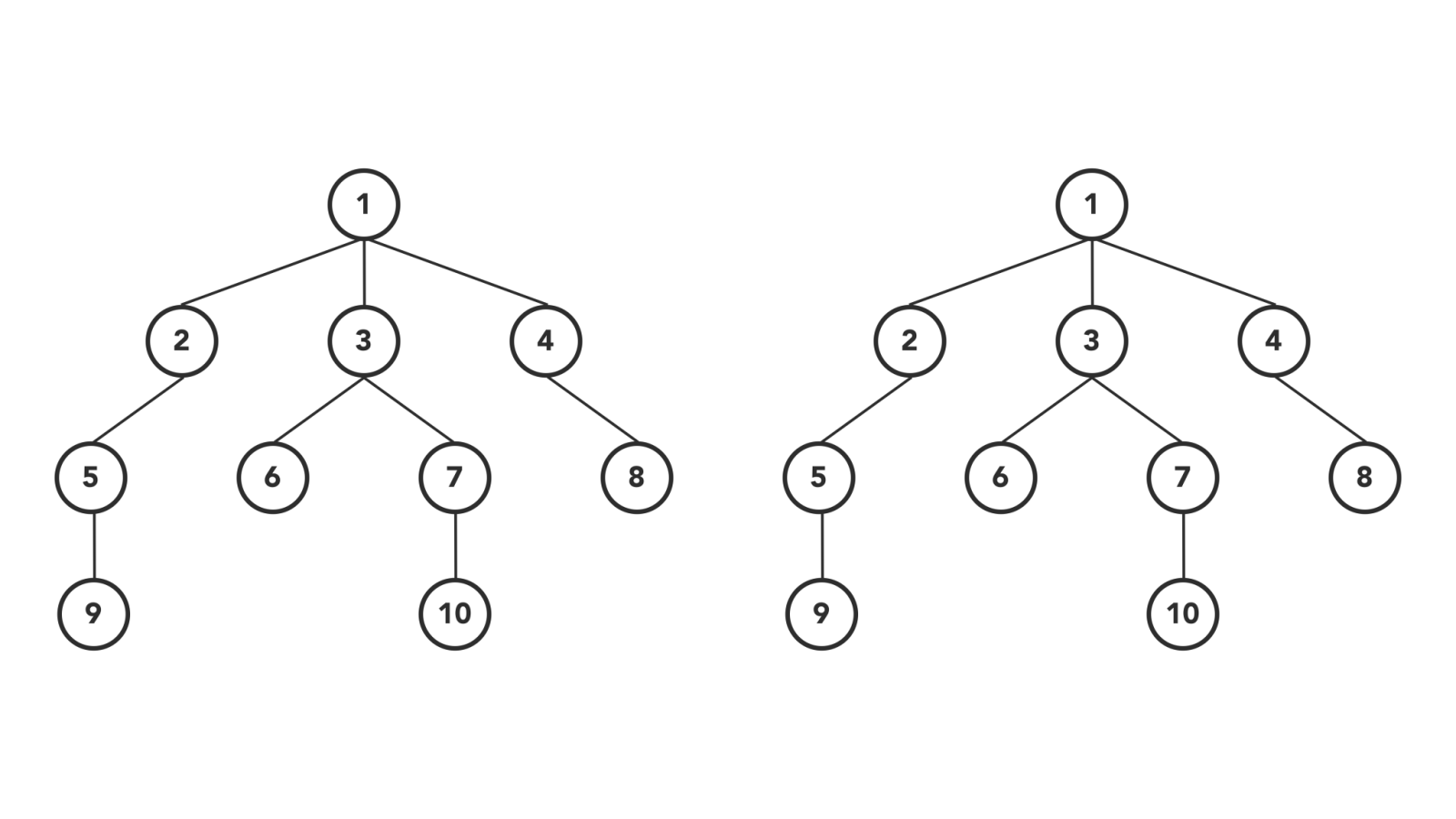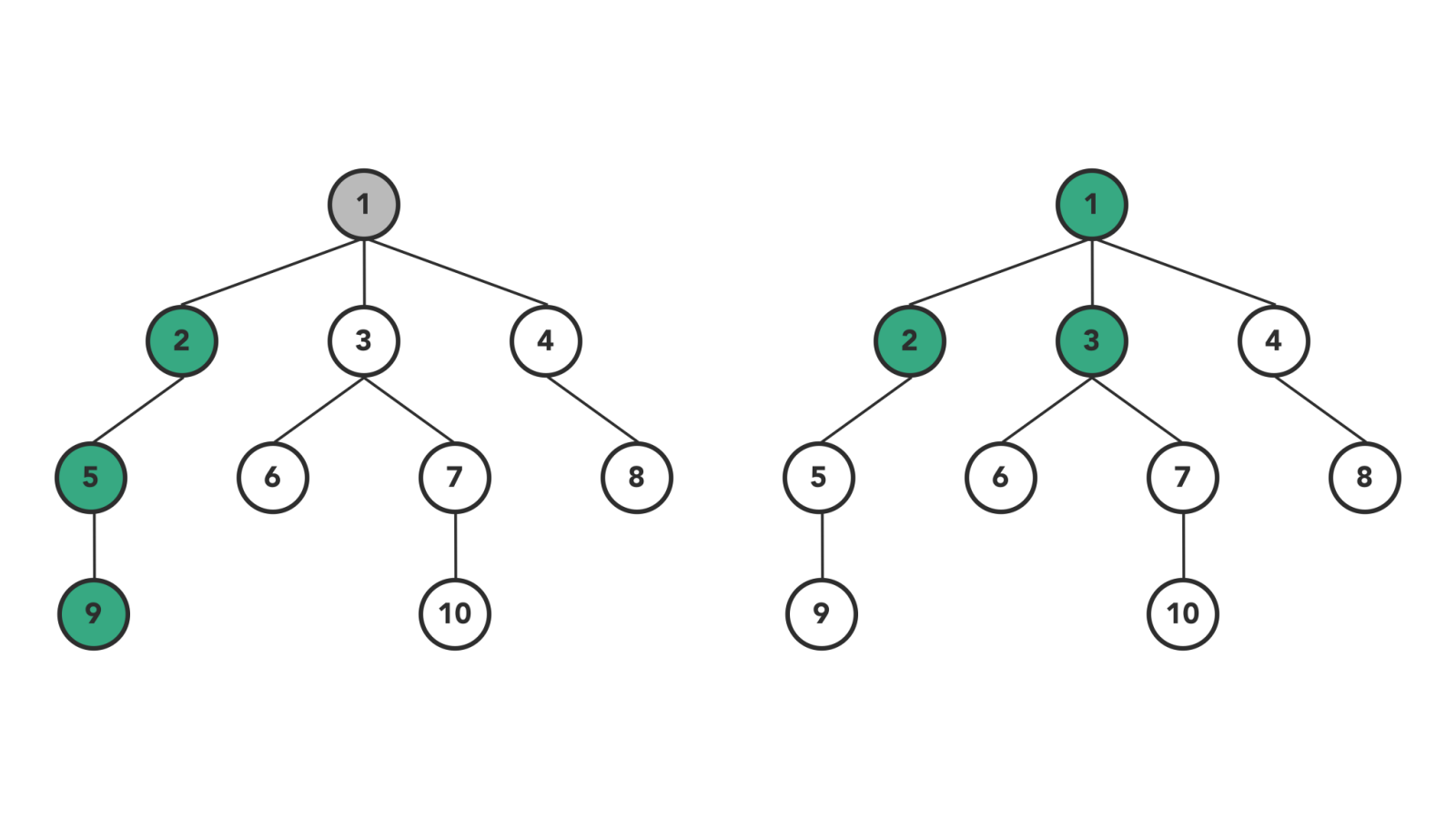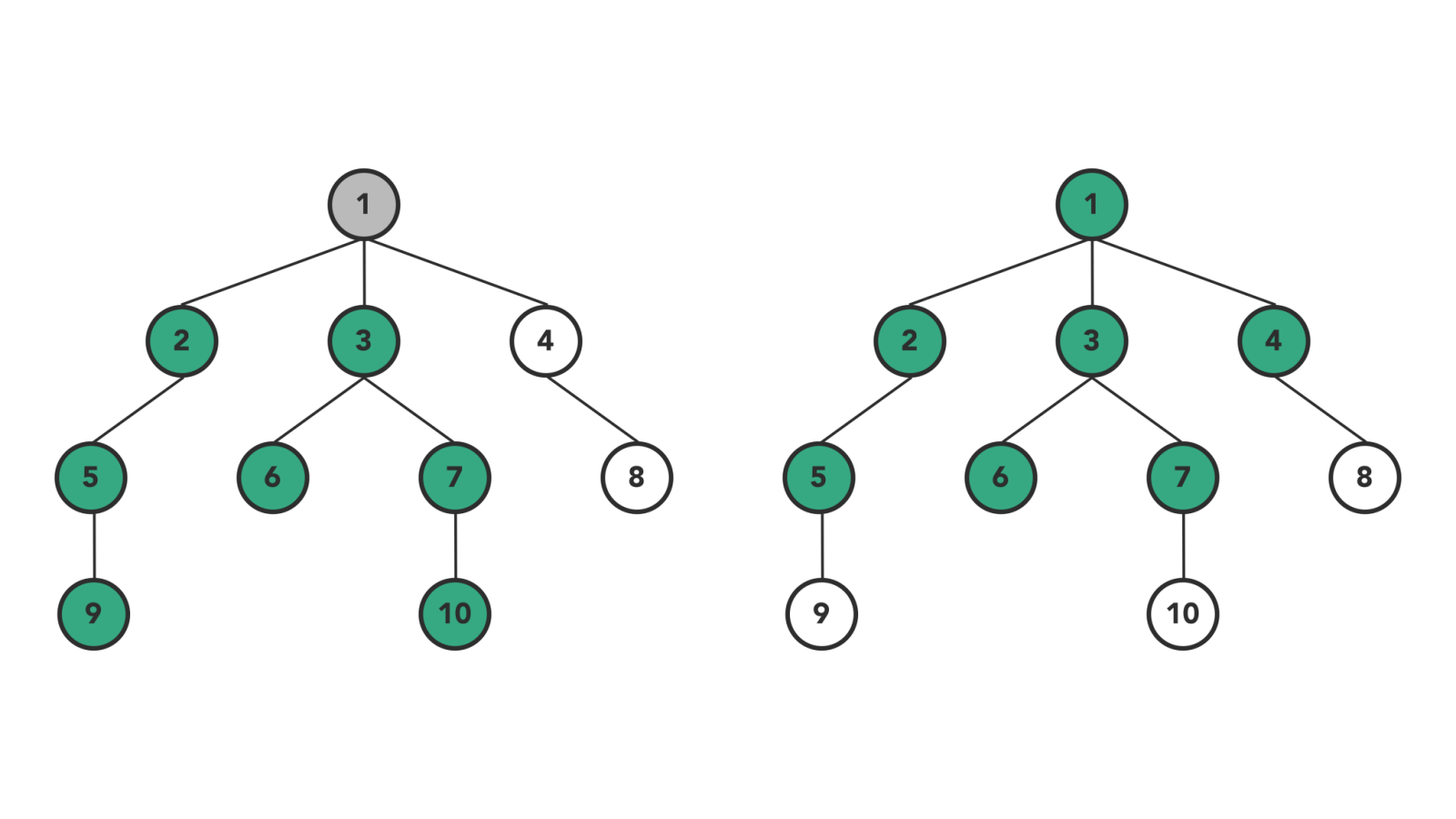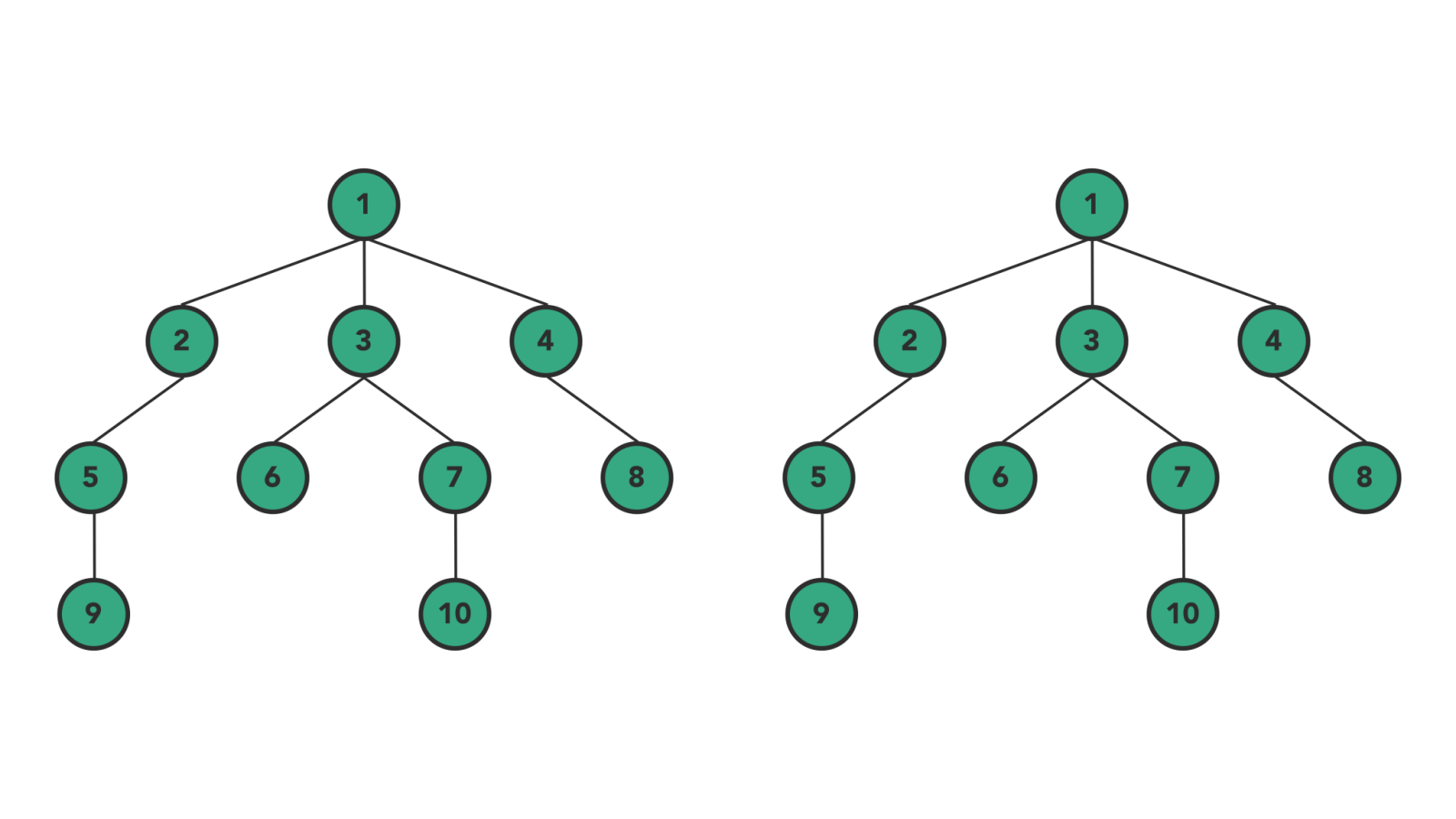
Types of Tree Traversal Algorithms

To understand tree traversal in a practical way, I will use Java to explain the algorithms. But these algorithms can be coded in your preferred programming language the same way we will do in Java.

Below is the blueprint of our node class that will act as the atomic member of the tree data structure. We will call it TreeNode, which is holding data as an integer value, left and right children of the same type(TreeNode). You can use any other data structure to keep as data under the TreeNode.

public class TreeNode {
	int data;
	TreeNode left;
	TreeNode right;

	public TreeNode(int data) {
		this.data = data;
		this.left = this.right = null;
	}
}

1. Inorder Traversal

Inorder traversal is the one the most used variant of DFS traversal of the tree.

As DFS suggests, we will first focus on the depth of the chosen node and then go to the breadth at that level. Therefore, we will start from the root node of the tree and go deeper-and-deeper into the left subtree in a recursive manner.

When we reach the left-most node with the above steps, then we will visit that current node and go to the left-most node of its right subtree, if it exists.

Same steps should be followed in a recursive manner to complete the inorder traversal. The order of those steps will be similar, in recursive function:

1. Go to the left subtree.
2. Visit node.
3. Go to the right subtree.

public void inorderTraversal(TreeNode root) {
	if (root != null) {
		inorderTraversal(root.left);
		System.out.print(root.data + " ");
		inorderTraversal(root.right);
	}
}

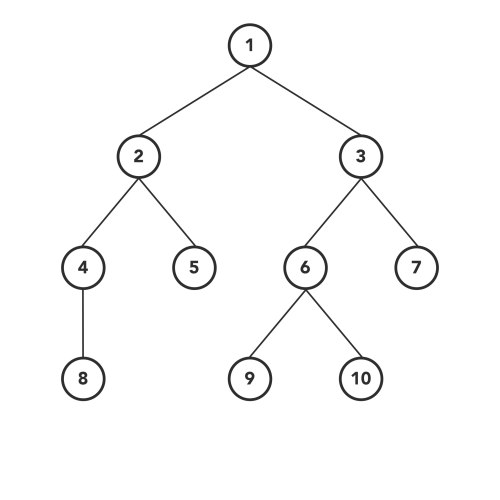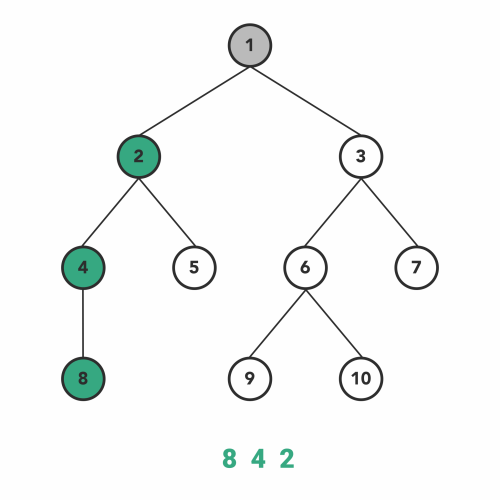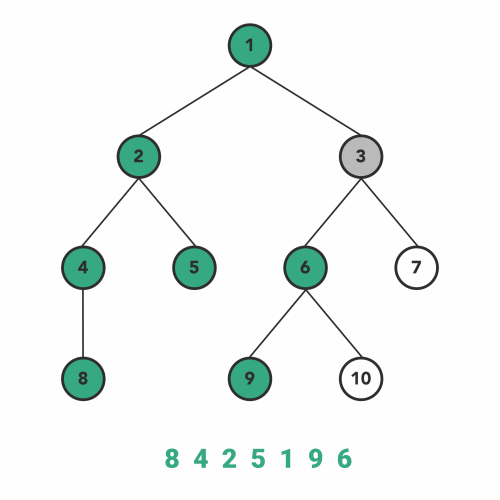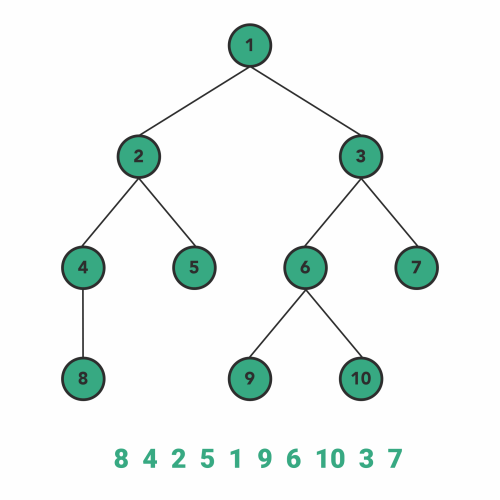
Inorder traversal of a binary search tree will always give you nodes in a sorted manner.

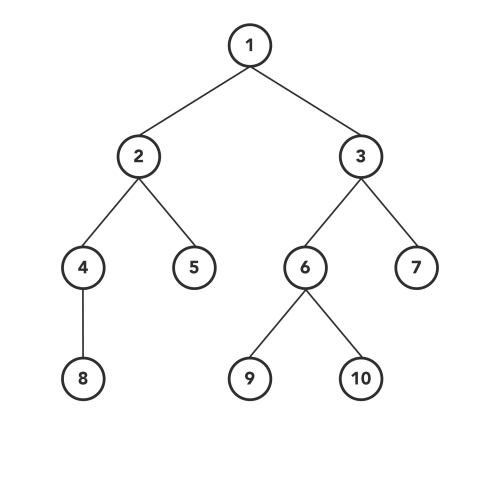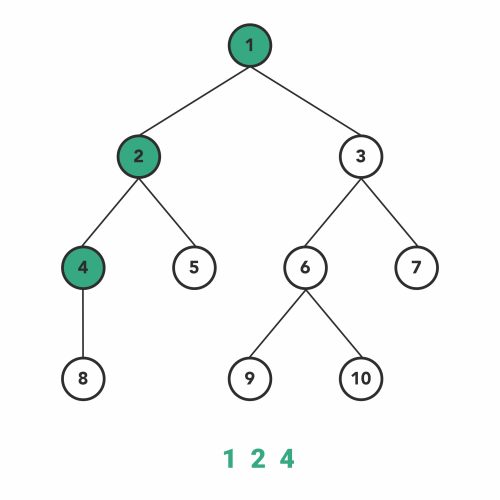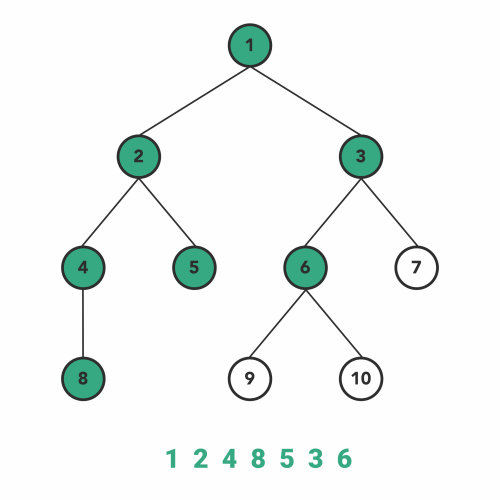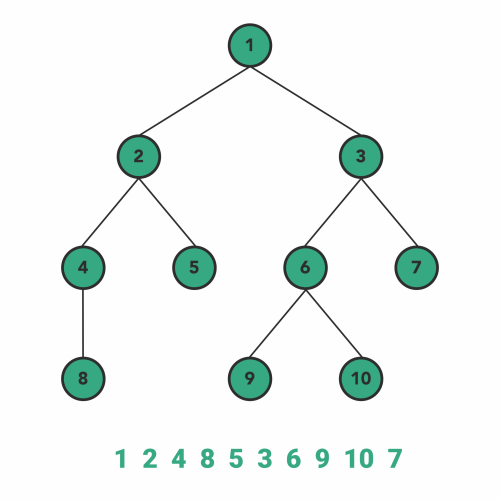
2. Preorder Traversal

Preorder traversal is another variant of DFS. The atomic operations in a recursive function are the same as inorder traversal but in a different order.

Here, we visit the current node first and then go to the left subtree. After covering every node of the left subtree, we will move toward the right subtree and visit in a similar fashion.

Order of the steps will be:

1. Visit node.
2. Go to the left subtree.
3. Go to the right subtree.

public void preorderTraversal(TreeNode root) {
	if (root != null) {
		System.out.print(root.data + " ");
		preorderTraversal(root.left);
		preorderTraversal(root.right);
	}
}

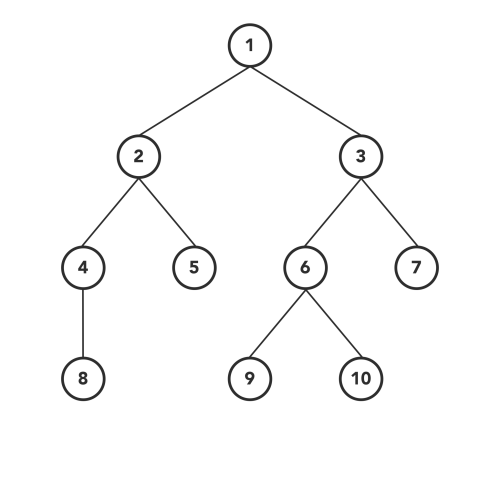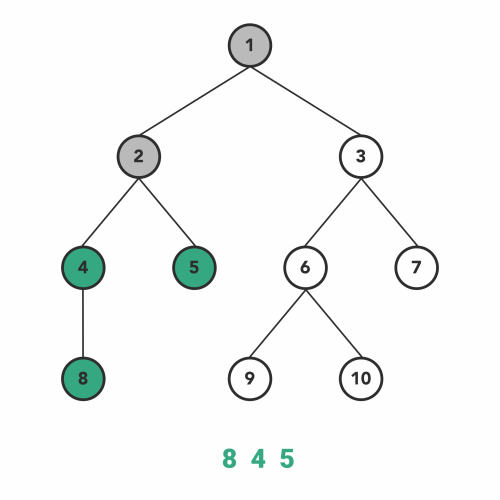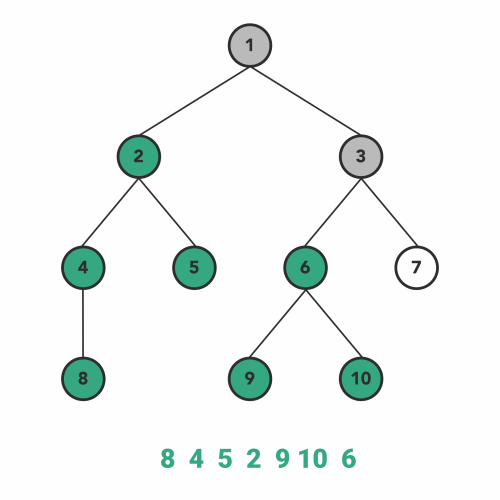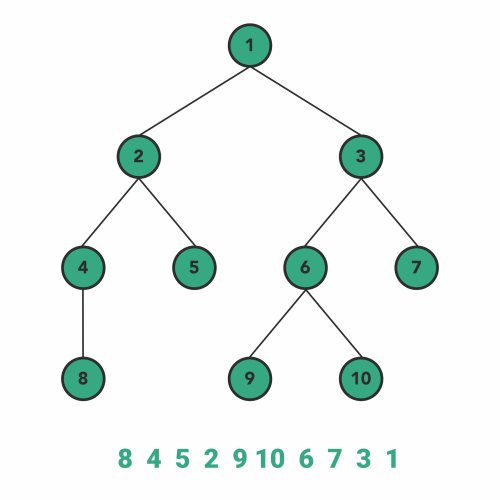
3. Postorder Traversal

A similar process goes for the postorder traversal, where we visit the left subtree and the right subtree before visiting the current node in recursion.

So, the sequence of the steps will be:

1. Go to the left subtree.
2. Go to the right subtree.
3. Visit the node.

public void postorderTraversal(TreeNode root) {
	if (root != null) {
		postorderTraversal(root.left);
		postorderTraversal(root.right);
		System.out.print(root.data + " ");
	}
}

4. Level Order Traversal

This is a different traversal than what we have covered above. Level order traversal follows breadth-first search to visit/modify every node of the tree.

As BFS suggests, the breadth of the tree takes priority first and then moves to depth. In simple words, we will visit all the nodes present at the same level one-by-one from left to right, and then it moves to the next level to visit all the nodes of that level.

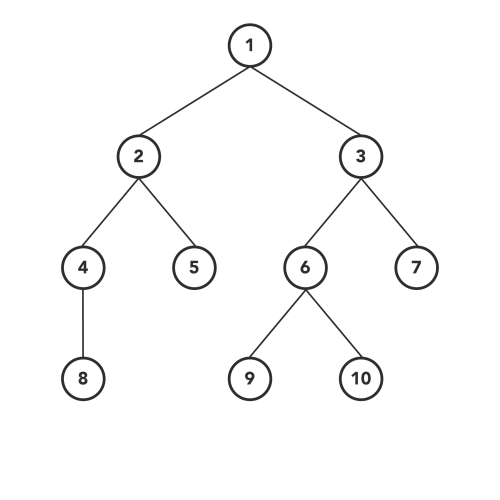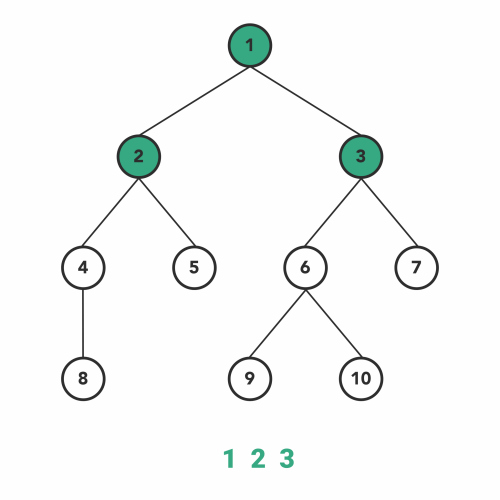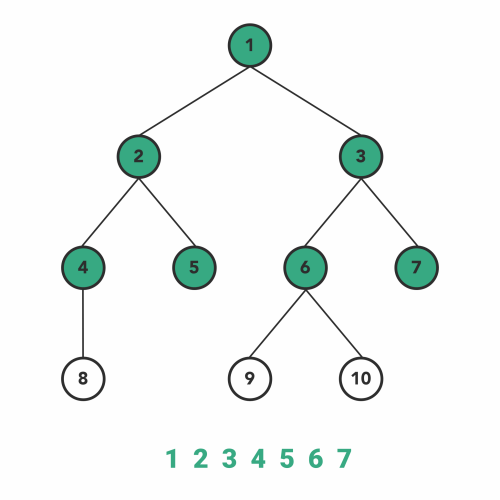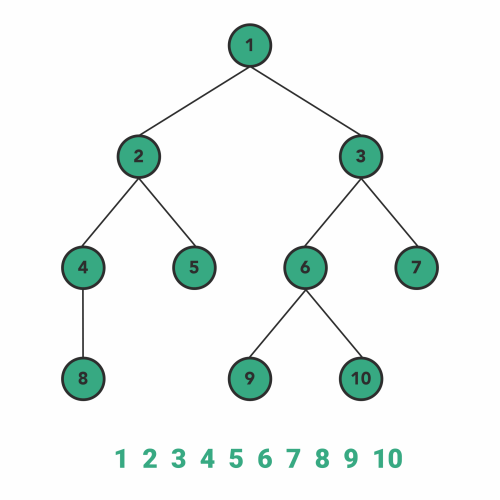
The implementation of level order traversal is slightly more challenging than the previous three traversals. We will use a Queue(FIFO) data structure to implement level order traversal, where after visiting a node, we put its left and right children to queue sequentially.

Here, the order of adding children in the queue is important, as we have to traverse left-to-right at the same level. Check the gist below for a better understanding.

public void levelorderTraversal(TreeNode root) {
	if (root == null) {
		return;
	}

	Queue<TreeNode> queue = new LinkedList<>();
	queue.add(root);

	while (!queue.isEmpty()) {
		TreeNode node = queue.remove();
		System.out.print(node.data + " ");

		if (node.left != null) {
			queue.add(node.left);
		}

		if (node.right != null) {
			queue.add(node.right);
		}
	}
}

More on Data Science: What Is Decision Tree Classification?

Classifying Tree Traversal Algorithms

As mentioned, tree traversal algorithms can be classified broadly in two categories:

• Depth-first search (DFS) algorithms.
• Breadth-first search (BFS) algorithms.

Depth-first search (DFS) algorithms have three variants:

1. Preorder traversal (current-left-right): This approach visits the current node before visiting any nodes inside left or right subtrees.
2. Inorder traversal (left-current-right): This approach visits the current node after visiting all nodes inside the left subtree, but before visiting any node within the right subtree.
3. Postorder traversal (left-right-current): This visits the current node after visiting all the nodes of left and right subtrees.

The breadth-first search (BFS) algorithm has one variant:

1. Level order traversal: This visits nodes level-by-level and in left-to-right fashion at the same level.

Check out the Github repository for detailed code. Remember, there are other tree traversal algorithms that classify as neither depth-first search nor breadth-first search. One such algorithm is the Monte Carlo tree search, which concentrates on the analysis of the most promising moves, expanding the search tree based on a random sampling of the search space.

Frequently Asked Questions