How to Implement Binary Search in Python

Binary search is an efficient algorithm to find an item from a sorted list of items. In comparison to other searching algorithms, binary search is the most popular algorithm for efficiently identifying the target element.

What Is Binary Search?

Binary search is a method of searching for the desired item in a sorted list of data. It is called binary because it splits an array into two halves as part of the algorithm.

Binary search is used to find an element in O(log(n)) time in a sorted array, where n is the size of an array. The pre-requisite of the binary search algorithm is that the array must be sorted. The algorithm uses two pointers, representing the left and right endpoints of an array. It compares the target value with the middle element of an array and then updates the array based on whether the target value is less than or greater than the middle element. The process is repeated until the element is found.

Binary search uses the divide and conquer algorithm for searching an element. Before diving into the implementation and how it works, it’s important to understand what binary and divide and conquer mean.

More on Data ScienceHow Database B-Tree Indexing Works

What Does Binary Mean?

In computer science, the term binary means 0,1 (we also call this bits). But in this algorithm, the term binary means if we have a long list of items and we split the list into two halves, then we call it a binary algorithm. In other words, it’s a search algorithm that divides the search interval into two halves at each step of the search until it either finds or determines that the target element is not in the list. Each division cuts the remaining portion of the list in half, which results in a binary tree structure.

Let’s look at an example.

Suppose we have a list of items inside an array. In the above definition, we understood that as part of the algorithm, binary means splitting an array into two halves. 

So, let’s divide the array into two halves while picturing the same thing in our minds.

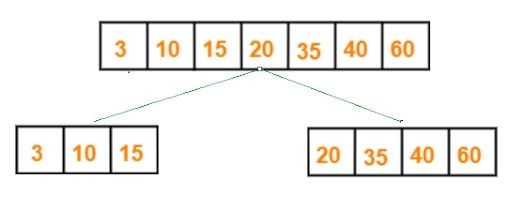
In the above example we have an array of sorted items.We divide the list into two halves. As a part of the binary search method, this is referred to as binary.

What Is Divide and Conquer?

Divide and conquer, as the names imply, mean splitting an array in half and merging. Let’s use the same example to explain conquering (merging) visually.

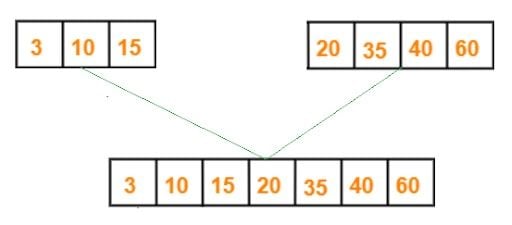
Divide is the term used to describe splitting an array into two halves in the first image, while conquer is the term used to describe the merging. Two split arrays are combined into one large array in the second image.

Is Binary Search Faster Than Linear Search?

When it comes to search algorithms, binary search is generally considered the most common one. Indeed, it’s a very useful algorithm to search an element from a list of sorted items.

Binary search has a time complexity of O(log(n)). In contrast, a linear search algorithm has a time complexity of O(n). As a result, linear search will take linear time as the size of the array increases. What does that mean? Suppose we have 1000 elements in an array and the target element is 999. A linear search algorithm will take O(1000) time to search an element, whereas binary search will take O(9) time to search an element. 

As a result, binary search is faster than linear search for large arrays. On every iteration, binary search eliminates half of the remaining elements from the search space, whereas linear search examines each element one by one.

We can use two different algorithms to search an element from the list. Those two algorithms are linear search and binary search. 

Linear search vs Binary Search

Linear search and binary search are the two common algorithms used for searching for an element in an array.

Linear is data that is connected one after another in a linear format. In the context of an algorithm, a linear search is a search that tries to find the element in a list one by one. Until a match is found, it will begin looking for an element from the beginning and move on to the next element. 

In binary search, we split the array into two halves and find the target element. Binary search doesn’t search for an element sequentially.

In terms of time and space efficiency, binary search is more effective because its time complexity is O(log(n)), whereas that of linear search is O(n). To compare the speeds, we use what’s called an asymptotic analysis, otherwise known as a run-time performance, which involves calculating the running time of the algorithm. 

The definition of logarithmic (log) in mathematics is: log(x) = y if 2^y = x. In computer science, we always assume the base is two for logs, i.e binary base two. Let’s look at some different values of x, and see the result.

• When x = 1, log(1) = 0        [2^0 =1]
• When x = 2, log(2) = 1,       [2^1 =2]
• When x = 4, log(4) = 2,       [2^2 =4]
• When x = 8, log(8) = 3,       [2^3 =8]
• When x = 16, log(16) = 4    [2^4 =16]

The observation from the above-calculated value is “When we double x, we are only increasing y by 1.” Now, what this really means is, as the input doubles, the elementary operations in the algorithm only increase by 1.

Let’s take the example of a binary search. Given an array of integer elements, search the target number in an array.

The binary search algorithm uses the divide and conquer algorithm for searching an element. It splits the array into two halves, and based on the target element and middle element of the array, it decides which half of the number will be present and repeats until the target element is not found.

Suppose the number of elements in an array is 8 (n = 8). As we know: log(8) = 3   [2^3 =8]

If we do two to the third power we will get eight. So, to find the target element in a list, the algorithm will take only three operations. This proves that with three operations we get our target element. Let’s analyze binary search and linear search graphically. The graph analysis of the linear search algorithm and binary search algorithm is as follows:

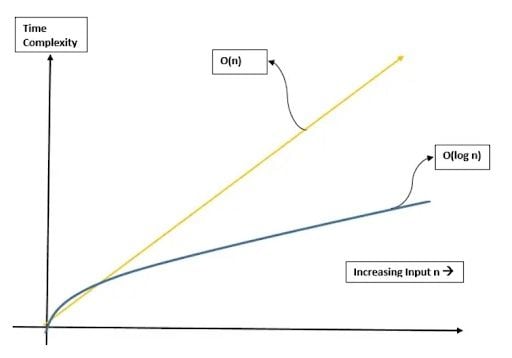
In the above figure, the yellow line is the time complexity of the linear search algorithm(O(n)). The blue line is the time complexity of the binary search algorithm(O(log n)).

How Does the Binary Search Algorithm Work?

There are three possible scenarios to find the element in an array or list.

• Search criteria = middle item: Item found.
• Search criteria < middle item: Search the first half of the array.
• Search criteria > middle item: Search the upper half of the array.

The steps followed by the binary search algorithm include:

1. Let n = length of the array, let min = 0 and max = n-1.
2. Calculate middle as the average of max and min, rounded down (so it’s an integer).
3. If array [middle] equals the target, then stop. You found it. Return guess.
4. If the middle was too low, that is, array [middle] < target, then set min = middle + 1.
5. Otherwise, the middle was too high. Set max = middle - 1.
6. Go back to step 2.

More on Data ScienceHow Do You Use Data Structures and Algorithms in Python

What Is Binary Search Algorithm’s Time-Space Complexity?

The time complexity of the binary search algorithm is logn, and the space complexity is constant (1) because we don’t use any extra auxiliary space to temporarily store data items.

How to Implement Binary Search in Python

The following is the code implementation of the binary search algorithm. Two solutions have been covered for the implementation.

In binary search, we look for an element X(target) in a sorted array by first comparing the target to the middle element of an array. If the target is less than the middle element, then we search the left half of the array. If the target is greater than the middle element, then we search the right half of the array. We then repeat this process, until we find our target. 

If the target element isn’t found in the list, it returns a null value based on the return type of the specific programming language. In Python, if the target value isn’t in the list, it returns -1. This is because most binary search implementations return the index of the target element and -1 is not a valid index.

Recursive Binary Search Implementation in Python 

A recursive implementation is the one that uses a function and calls itself to search for the target element. Here is an example implementation of binary search in Python using recursion.

def binarySearch(array, target):
    return binarySearchHelper(array, target, 0, len(array)-1);
def binarySearchHelper(array, target, left, right):
    if left > right:
        return -1
    middle = (left+right) // 2
    potentialMatch = array[middle]
    if target == potentialMatch:
            return middle
    elif target < potentialMatch:
        return binarySearchHelper(array, target, left, middle - 1)
    else:
        return binarySearchHelper(array, target, middle + 1, right)

In this implementation, the function binarySearchHelpertakes four parameters: the array to search, the target element to find, the lowest index to search in the array (initially 0), and the highest index to search in the array (initially len(arr) - 1).

If we recall all the steps of binary search working, the algorithm will calculate the middle value and compare with the target element and if it doesn’t match, it will move the pointer left or right based on the middle value. The function uses recursion to call itself by passing new left and right values. The process continues until the target element found or search space is empty.

Iterative Binary Search Implementation in Python.

An iterative implementation is the one that uses a loop to search for the target element. Here’s an example implementation of binary search in Python using iteration.

def binarySearch(array, target):
    left, right = 0, len(array)-1
    while left <= right:
        middle = (left+right) // 2
        potentialMatch = array[middle]
        if target == potentialMatch:
            return middle
        elif target < potentialMatch:
            right = middle - 1
        else:
            left = middle + 1
    return -1

In this implementation, the function binarySearch takes two parameters: the array to search, the target element to find. The function initializes the ‘left’ and ‘right’ indices to the beginning and the end of the array respectively. 

The function enters the while loop. At each iteration, the middle value is calculated until it reaches the matching target number. Once it does, the algorithm will return the target element index. If the target number is less than the middle element, the function updates the left pointer to middle index +1. If the target element is greater than the middle element, the function updates the right pointer to middle index -1.

If the target element isn’t found in the array, the function returns -1. 

Advantages of Binary Search

Binary search is a powerful and efficient algorithm that can be used to search datasets of any size. Its advantages include:

• It’s a very efficient search algorithm, especially when dealing with large data sets.
• It’s a simple algorithm to implement. It only requires basic loops and conditional statements, and it can be implemented with any programming language.
• It can be used on a wide variety of data structures, including sorted arrays and binary trees. This makes it a versatile searching algorithm.
• It doesn’t require additional memory to perform its search.
• It’s guaranteed to find the target element if it exists in the list. If the target element doesn’t exist in the list, it returns -1.

Binary search is most useful in the following situations:

• When dealing with larger data sets. Binary search is much faster than other search algorithms. So, we can use this algorithm when we need to search in a huge data set.
• The search is frequent. If a particular search needs to be performed multiple times on the same data set, then it may be worth using binary search to improve overall performance of the application.

Disadvantages of Binary Search

Binary search does have some limitations, and it may not be suitable for all situations. It’s important to consider the size and nature of the data set.  The disadvantages of binary search include:

• Binary search can only be used on sorted data.
• Sorting can be an expensive operation and can take additional time and space.
• Binary search requires random access to elements in the data set, which means that it’s not suitable for linked lists and data structures that don’t use random access.
• It can be memory inefficient in recursive implementation. When a function calls itself recursively, on every call, a new layer is added on the stack. This can be a problem if you’re operating in a memory-constrained environment.
• Binary search is time-consuming when the data is dynamic.

And that’s the binary search algorithm.