How Database B-Tree Indexing Works 

When we think about the performance of a database, indexing is the first thing that comes to the mind. Here, we’re going to look into how database indexing works on a database. 

The architectural details described below are for the SQLite 2.x database architecture. You can find out the back end implementation of SQLite 2.5.0 with tests.

What Is B-tree?

A B-tree is a data structure that provides sorted data and allows searches, sequential access, attachments and removals in sorted order. The B-tree is highly capable of storing systems that write large blocks of data. The B-tree simplifies the binary search tree by allowing nodes with more than two children. Below is a B-tree example.

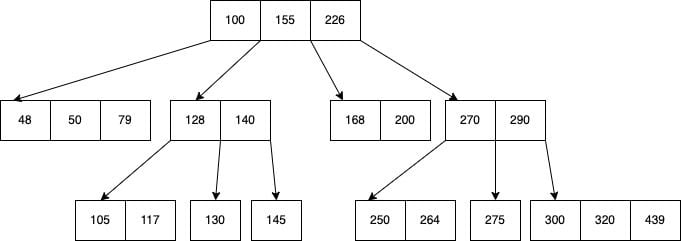
B-tree stores data such that each node contains keys in ascending order. Each of these keys has two references to another two child nodes. The left side child node keys are less than the current keys, and the right side child node keys are more than the current keys. If a single node has “n” number of keys, then it can have maximum “n+1” child nodes.

More on Data ScienceTop 10 Machine Learning Algorithms for Beginners

Why B-Tree Indexing Is Necessary

Imagine that you need to store a list of numbers in a file and search a given number on that list. The simplest solution is to store data in an array and append values when new values come in. But if you need to check if a given value exists in the array, then you need to search through each of the array elements one by one and check whether the given value exists. 

If you’re lucky, you might find the given value in the first element. But in the worst case scenario, the value could be the last element in the array. We denote this worst case as O(n) in asymptotic notation. This means if your array size is “n,” at most, you need to complete “n” number of searches to find a given value in an array.

How could you improve this time? The easiest solution is to sort the array and use binary search to find the value. Whenever you insert a value into the array, it should maintain order. The search starts by selecting a value from the middle of the array. Then it compares the selected value with the search value. If the selected value is greater than the search value, then it ignores the left side of the array and searches the value on the right side, and vice versa.

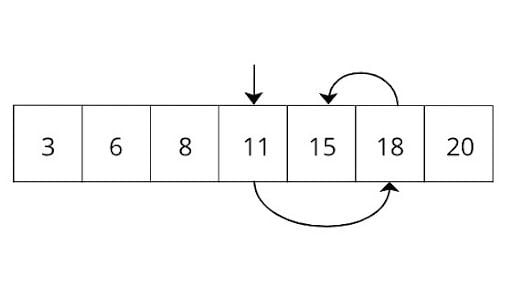
Here, we try to search key 15 from the array 3,6,8,11,15 and 18, which is already in sorted order. If you do a normal search, then it will take five units of time, since the element is in the fifth position. But in a binary search, it will only take three searches.

If we apply this binary search to all of the elements in the array, then it would be as follows.

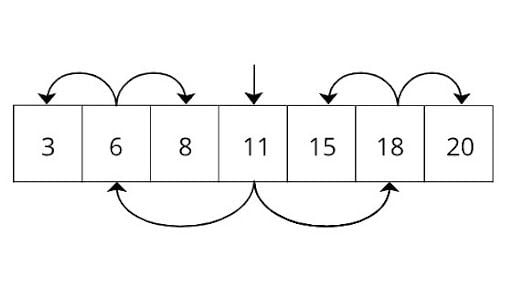
Look familiar? It’s a binary tree. This is the simplest form of the B-tree. For a binary tree, we can use pointers instead of keeping data in a sorted array. Mathematically, we can prove that the worst case search time for a binary tree is O(log(n)). 

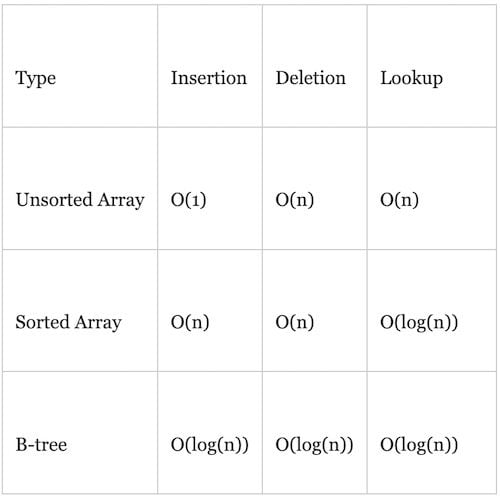
The concept of Binary tree can be extended into a more generalized form, which is known as B-tree. Instead of having a single entry for a single node, B-tree uses an array of entries for a single node and has references to a child node for each of these entries. Below are some time complexity comparisons of each pre-described method.

B+Tree vs. B-Tree: What’s the Difference?

B+ tree is another data structure that’s used to store data and looks almost the same as the B-tree. The only difference is that B+ tree stores data on the leaf nodes. This means that all non-leaf node values are duplicated in leaf nodes again. Below is a sample B+tree.

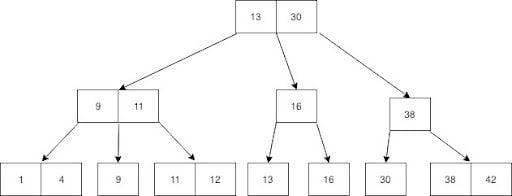
 The 13, 30, 9, 11, 16 and 38 non-leaf values are again repeated in leaf nodes. 

Leaf nodes include all values and all of the records are in sorted order. B+tree allows you to do the same search as B-tree, but it also allows you to  travel through all the values in a leaf node if we put a pointer to each leaf node as follows.

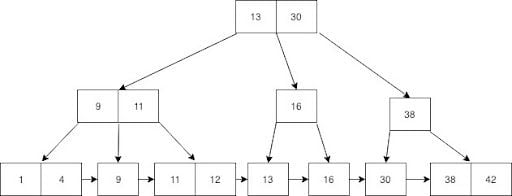
How Is B-Tree Indexing Used in a Database?

When B-tree comes to the database indexing, this data structure gets a little complicated because it doesn’t just have a key, it also has a value associated with the key. This value is a reference to the actual data record. The key and value together are called a payload.

Assume the following three-column table needs to be stored on a database:

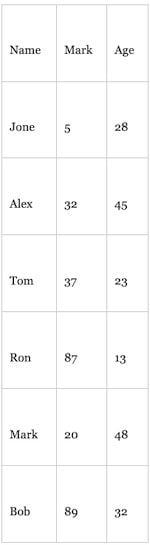
First, the database creates a unique random index (or primary key) for each of the given records and converts the relevant rows into a byte stream. Then, it stores each of the keys and record byte streams on a B+tree. Here, the random index used as the key for indexing. The key and record byte stream is altogether known as Payload. The resulting B+tree could be represented as follows.

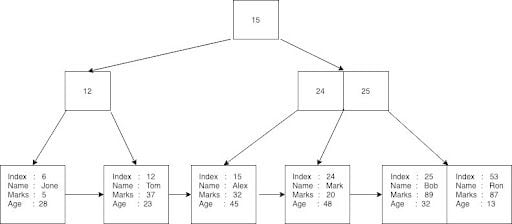
Here you can see that all records are stored in the leaf nodes of the B+tree and index and are used as the key to create a B+tree. No records are stored on non-leaf nodes. Each of the leaf nodes references the next record in the tree. A database can perform a binary search by using the index or sequential search by searching through every element by only traveling through the leaf nodes.

If no indexing is used, then the database reads each of these records to find the given record. When indexing is enabled, the database creates three B-trees for each of the columns in the table, as follows. Here the key is the B-tree key used to index. The index is the reference to the actual data record:

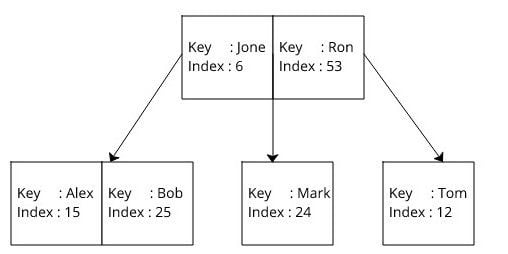
When indexing is used first, the database searches a given key in correspondence to B-tree and gets the index in O(log(n)) time. Then, it performs another search in B+tree by using the already found index in O(log(n)) time and gets the record.

Each of these nodes in B-tree and B+tree is stored inside the pages. Pages are fixed in size. Pages have a unique number starting from one. A page can be a reference to another page by using a page number. At the beginning of the page, page meta details such as the rightmost child page number, first free cell offset and the first cell offset stored. There can be two types of pages in a database:

1. Pages for indexing: These pages store only an index and a reference to another page.
2. Pages to store records: These pages store the actual data and the page should be a leaf page.

Using SQLite B-Tree Indexing

The basic syntax to create a B-tree index as follows:

CREATE INDEX index_name ON table_name;

There are three kinds of indexing methods used in SQLite.

1. Single Column Index

Here, indexes are created based on one table column. Only a single B-tree is created for indexes. The syntax is as follows.

CREATE INDEX index_name ON table_name (column_name);

2. Unique Index

Unique indexes aren’t allowed to store duplicate values for the column that uses indexing. The syntax can be written as follows:

CREATE UNIQUE INDEX index_name on table_name (column_name);

3. Composite Index

This type of index can have multiple indexes. For each of the index columns, There exists a Btree. The following is the syntax for composite index:

CREATE INDEX index_name on table_name (column1, column2);

More on Data ScienceWhat Is a Data Set?

Advantages of B-Tree Indexing

Databases should have an efficient way to store, read, and modify data. B-tree provides an efficient way to insert and read data. In actual database implementation, the database uses both B-tree and B+tree together to store data. B-tree used for indexing and B+tree used to store the actual records. B+tree provides sequential search capabilities in addition to the binary search, which gives the database more control to search non-index values in a database.