Data Standardization: How to Do It and Why It Matters

Data standardization is the conversion of data into a standard, uniform format, making it consistent across different data sets and easier to understand for computer systems. It’s often performed when pre-processing data for input into machine learning or statistical models. Standardizing data can enhance data quality and accuracy, which helps users make reliable data-driven decisions.

Some machine learning developers tend to standardize their data blindly before every machine learning model, without making the effort to understand why it must be used, or even if it’s needed or not. So the goal of this article is to further explain how, why and when to standardize data.

What Is Data Standardization?

Data standardization comes into the picture when features of the input data set have large differences between their ranges, or simply when they are measured in different units (e.g., pounds, meters, miles, etc.).

These differences in the ranges of initial features cause trouble for many machine learning models. For example, for the models that are based on distance computation, if one of the features has a broad range of values, the distance will be governed by this particular feature.

To illustrate this with an example: Say we have a two-dimensional data set with two features, height in meters and weight in pounds, that range respectively from 1 to 2 meters and 10 to 200 pounds. No matter what distance-based model you perform on this data set, the weight feature will dominate over the height feature and will have more contribution to the distance computation, just because it has bigger values compared to the height. So, to prevent this problem, transforming features to comparable scales using standardization is the solution.

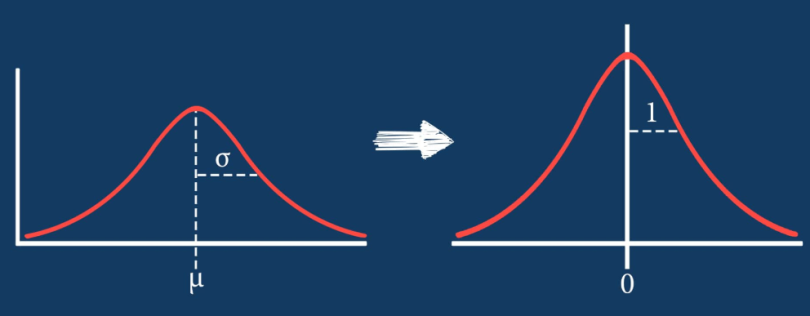
How to Standardize Data

Z-score normalization, or standardization, is one of the most popular methods to standardize data. With this method, data is transformed to have a mean of 0 and a standard deviation of 1, giving all data points the same scale. 

Z-score normalization is done by subtracting the mean and dividing by the standard deviation for each data value of each feature.

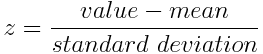
In the z-score normalization formula:

• z = new, standardized data value
• value = original data value

When and Why to Standardize Data

As seen above, for distance-based models, standardization is performed to prevent features with wider ranges from dominating the distance metric. But the reason we standardize data is not the same for all machine learning models, and differs from one model to another.

So, when should you standardize your data, and why?

1. Before Principal Component Analysis (PCA)

In principal component analysis, features with high variances or wide ranges get more weight than those with low variances, and consequently, they end up illegitimately dominating the first principal components (components with maximum variance). I used the word “illegitimately” here because the reason these features have high variances compared to the other ones is just because they were measured in different scales.

Standardization can prevent this by giving the same weightage to all features.

2. Before Clustering

Clustering models are distance-based algorithms. In order to measure similarities between observations and form clusters they use a distance metric. So, features with high ranges will have a bigger influence on the clustering. Therefore, standardization is required before building a clustering model.

3. Before K-Nearest Neighbors (KNN)

K-nearest neighbors is a distance-based classifier that classifies new observations based on similar measures (e.g., distance metrics) with labeled observations of the training set. Standardization makes all variables contribute equally to the similarity measures.

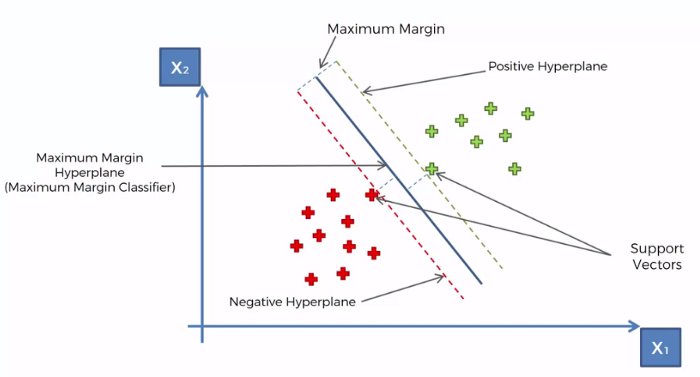
4. Before Support Vector Machine (SVM)

Support vector machine tries to maximize the distance between the separating plane and the support vectors. If one feature has very large values, it will dominate over other features when calculating the distance. Standardization gives all features the same influence on the distance metric.

5. Before Measuring Variable Importance in Regression Models

You can measure variable importance in regression analysis by fitting a regression model using the standardized independent variables and comparing the absolute value of their standardized coefficients. But, if the independent variables are not standardized, comparing their coefficients becomes meaningless.

6. Before Lasso and Ridge Regressions

Lasso and ridge regressions place a penalty on the magnitude of the coefficients associated with each variable, and the scale of variables will affect how much of a penalty will be applied on their coefficients. Coefficients of variables with a large variance are small and thus less penalized. Therefore, standardization is required before fitting both regressions.

Cases When Standardization Is Not Needed

Logistic Regressions and Tree-Based Models

Logistic regressions and tree-based algorithms such as decision trees, random forests and gradient boosting are not sensitive to the magnitude of variables. So standardization is not needed before fitting these kinds of models.

Benefits of Data Standardization 

Data standardization transforms data into a consistent, standard format, making it easier to understand and use — especially for machine learning models and across different computer systems and databases. Standardized data can facilitate data processing and storage tasks, as well as improve accuracy during data analysis. Plus, making data more navigable by standardizing it can reduce costs and save time for businesses.

Normalization vs. Data Standardization

Normalization involves scaling data values in a range between 0 and 1 ([0,1]), or between -1 and 1 ([-1, 1]) for negative values. Data standardization, on the other hand, involves scaling data values so that they have a mean of 0 and standard deviation of 1. Also, since normalization has a restricted value range and standardization does not, normalization is more likely to be affected by outliers, where standardization is less likely to be affected by outliers.

Normalization is useful for when a feature distribution is unknown or non-normal/non-Gaussian, while standardization is useful for when features follow a normal/Gaussian distribution.

Wrapping Up Data Standardization

As you can see, when to standardize and when not to depend on which model you want to use and what you want to do with it. Therefore, it’s very important for a machine learning developer to understand the internal functioning of machine learning algorithms, to be able to know when to standardize data and how to build a successful machine learning or statistical model.

Note: The list of models and methods for when standardization is required presented in this post is not exhaustive.

Frequently Asked Questions