Extrapolation is an inexpensive and effective method you can use to predict future values and trends in data, as well as gain insight into the behavior of complex environments. Extrapolation is especially helpful for time series and geospatial analysis due to the technique’s ability to take into account the impact of temporal and spatial factors on the data.
Using extrapolation techniques, you can calculate unobserved values by extending a known sequence of values in the data set.
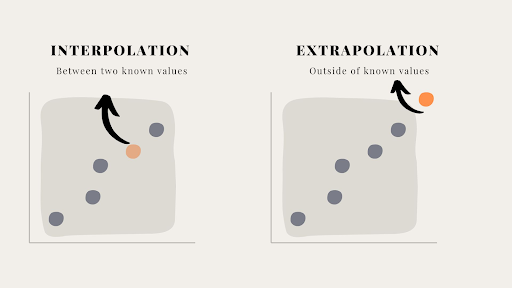
Extrapolation vs. Interpolation: What’s the Difference?
Extrapolation is often mistaken for interpolation. The two use the same techniques to estimate unknown values but differ in some key areas. If the estimated values are derived within two known values, then it’s an interpolation. However, if the predicted values fall outside of the data set, then it’s extrapolation.
Common Extrapolation Methods
There are different types of extrapolation for predicting and evaluating trends in data. The following two are the most widely used extrapolation methods.
- Linear Extrapolation: This is the most basic form of extrapolation that uses a linear equation to predict future outcomes. This method is best suited for predictions close to the given data. We simply draw a tangent line from the last point to extend it beyond the known values.
- Polynomial Extrapolation: This method uses a polynomial equation to make predictions about future values. We use polynomial extrapolation when the data points exhibit a non-linear trend. This is more complex than linear extrapolation and we can use it to make more accurate predictions.
How Does Extrapolation Work?
Extrapolation is basically a forecasting method common in time series analysis. The following example uses linear extrapolation to predict sales.
Let’s take an example of a company’s sales in 2020 and 2021, then extrapolate what the sales will be in 2022.
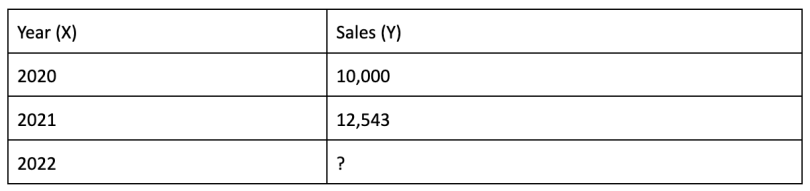
To find the value of 2022 using extrapolation, with the given sales records of the past two years, we first need to calculate the slope.
m = (y2 - y1) / (x2 - x1)
After that, we apply a line equation.
(y = y1 + m · (x - x1))
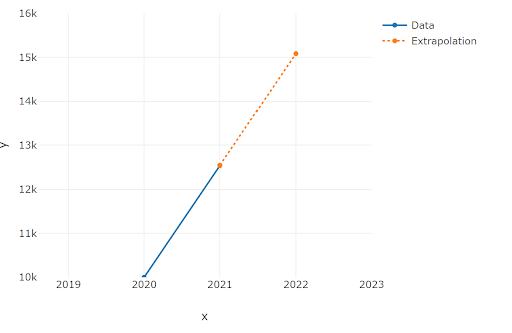
We can then find the extrapolated value for 2022 by plugging the values into the equations above. We conclude that sales will be $15,086.
What Are the Benefits of Extrapolation?
Extrapolating is a powerful tool to help us make data-informed predictions and understand trends. Here are some reasons why we use extrapolation methods.
- If we’re worried that expert forecasts are biased but we don’t know much about the situation, extrapolation might be the best option.
- Extrapolation is inexpensive and straightforward, which means you can run the modeling as much as you need to in order to have multiple predictions.
- When you’re looking at multiple scenarios that are an important element in the forecast, such as economic trends and change policies, extrapolation can help the process.
- Extrapolation can help identify potential risks or future opportunities.
- Extrapolation helps you identify patterns in data and make informed decisions.
What Are the Risks of Extrapolation?
Although the process of extrapolation is simple and straightforward, its accuracy and reliability depend on the trends present in the data set. Thus, careful consideration of the data set and the values it contains can help you mitigate larger errors in forecasting future trends. It’s also essential to use various methods when extrapolating to help reduce errors and ensure that the extrapolation is based on a complete and accurate understanding of the data.
