K-Nearest Neighbor Algorithm: An Introduction

K-nearest neighbor (KNN) is a simple algorithm that stores all available cases and classifies new data or cases based on a similarity measure. It is mostly used to classify a data point based on how its neighbors are classified.

Let’s break it down with a wine example examining two chemical components called rutin and myricetin. Consider a measurement of the rutin vs. myricetin level with two data points — red and white wines. After being tested, they’re placed on a graph based on how much rutin and how much myricetin chemical content is present in the wines.

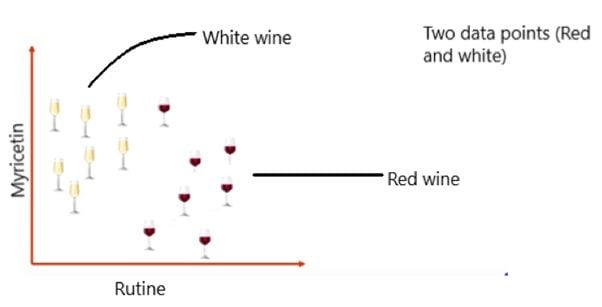
The “K” in KNN is a parameter that refers to the number of nearest neighbors to include in the majority of the voting process.

Now suppose we add a new glass of wine in the data set, and we want to know whether this new wine is red or white.

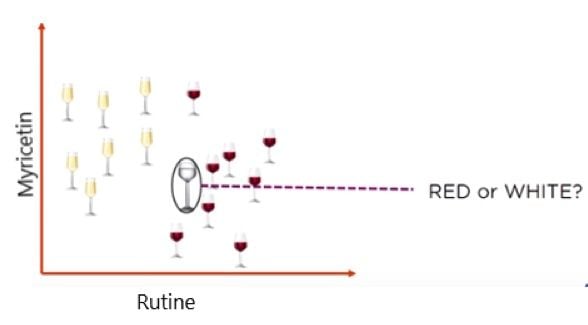
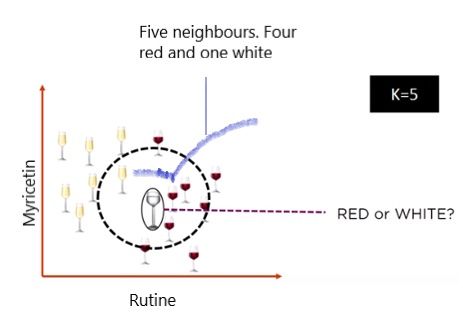
To do so, we need to find out what the neighbors are in this case. Let’s say k = 5, and the new data point is classified by the majority of votes from its five neighbors. The new point would be classified as a red wine since four out of five neighbors are red.

Determining the K-Nearest Neighbor Algorithm’s ‘K’ Value

The “K” in KNN algorithm is based on feature similarity. Choosing the right value for K is a process called parameter tuning, which improves the algorithm accuracy. Finding the value of K is not easy.

More on Machine LearningAn In-Depth Guide to Supervised Machine Learning Classification

How to Define a ‘K’ Value

Below are some ideas on how to pick the value of K in a K-nearest neighbor algorithm:

1. There is no structured method for finding the best value for K. We need to assume that the training data is unknown and find the best value through trial and error.
2. Choosing smaller values for K can be noisy and will have a higher influence on the result.
3. Larger values of K will have smoother decision boundaries, which means a lower variance but increased bias. Also, it can be computationally expensive.
4. Another way to choose K is through cross-validation. One way to select the cross-validation data set from the training data set is to take a small portion from the training data set and call it a validation data set. Then use the same process to evaluate different possible values of K. In this way, we are able to predict the label for every instance in the validation set using K equals to one, K equals to two, K equals to three, and so on. Then we look at what value of K gives us the best performance on the validation set. From there, we can take that value and use that as the final setting of our algorithm to minimize the validation error.
5. In general practice, choosing the value of K is k = sqrt(N) where “N” stands for the number of samples in your training data set.
6. Try to keep the value of K odd in order to avoid confusion between two classes of data.

How Does a K-Nearest Neighbor Algorithm Work?

In the classification setting, the K-nearest neighbor algorithm essentially boils down to forming a majority vote between the K with most similar instances to a given unseen observation. Similarity is defined according to a distance metric between two data points. A popular one is the Euclidean distance method.

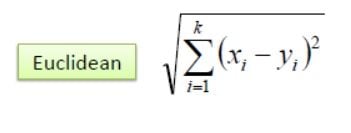
Other methods are Manhattan, Minkowski, and Hamming distance methods. For categorical variables, the Hamming distance must be used.

Let’s take a small example examining age vs. loan amount.

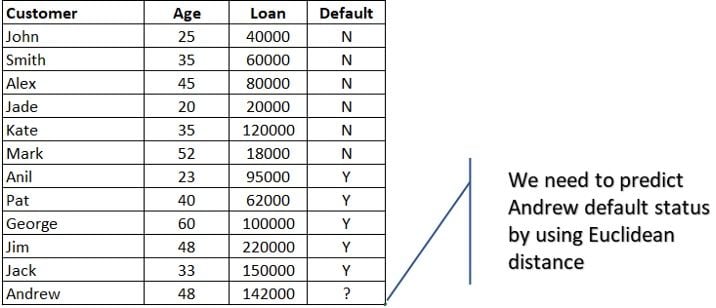
We need to predict Andrew’s default status — either yes or no.

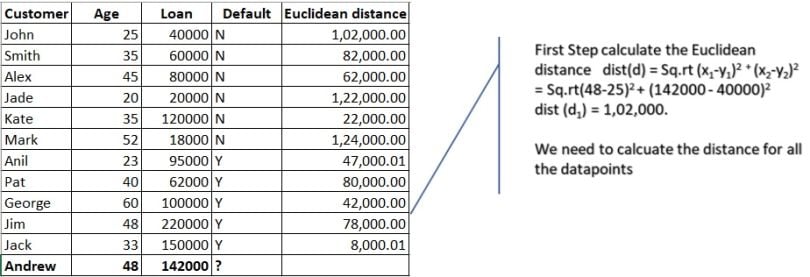
Then calculate the Euclidean distance for all the data points.

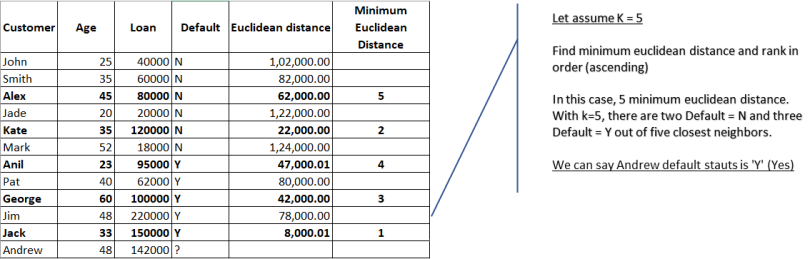
With K=5, there are two Default=N and three Default=Y out of five closest neighbors. We can safely say the default status for Andrew is “Y” based on the majority similarity in three points out of five.

KNN is also a lazy learner because it doesn’t learn a discriminative function from the training data but “memorizes” the training data set instead.

Become a Machine Learning ExpertMachine Learning A-Z™: Hands-On Python & R in Data Science

Computing K-Nearest Neighbor Distance Metrics 

Hamming Distance

Hamming distance is mostly used in text data, which calculates the distance between two binary vectors. Here, binary vector means the data represented in the form of binary digits 0 and 1. It is also called binary strings.

Mathematically, it’s represented by the following formula:

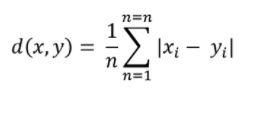
Euclidean Distance

Euclidean distance is the most popular distance measure. It helps to find the distance between two real-valued vectors, like integers or floats. Before using Euclidean distance, we must normalize or standardize the data, otherwise, data with larger values will dominate the outcome.

Mathematically, it’s represented by the following formula.

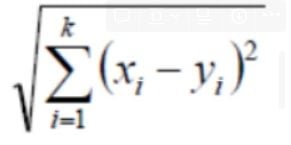
Manhattan Distance

Manhattan distance is the simplest measure, and it’s used to calculate the distance between two real-valued vectors. It is called “Taxicab” or “City Block” distance measure.

If we start from one place and move to another, Manhattan distance will calculate the absolute value between starting and destination points. Manhattan is preferred over Euclidean if the two data points are in an integer space.

The Manhattan distance between two points (X1, Y1) and (X2, Y2) is represented by |X1 – X2| + |Y1 – Y2|.

Minkowski Distance

Minkowski distance is used to calculate the distance between two real value vectors. It is a generalized form for Euclidean and Manhattan distance. In addition, it adds a parameter “p,” which helps to calculate the different distance measures.

Mathematically it’s represented by the following formula. Note that in Euclidean distance p = 2, and p =1 if it is Manhattan distance.

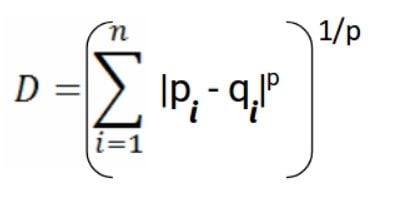
K-Nearest Neighbor Applications in Machine Learning

KNN is widely used in machine learning applications. Some of the most famous use cases are mentioned below.

Recommendation Engine

A recommendation engine provides product suggestions or services to the user based on the data. KNN has been used in the recommendation system to identify items or products based on the user’s data. However, it is unsuitable for high dimensional data due to computation. However, it is an excellent choice for the baseline approach.

Concept Search

Concept search involves searching semantically similar documents and classifying documents containing similar topics. In today’s world, data is generated exponentially, and it creates tons of documents. Each of those documents contains key concepts. Assume we have a use case to extract these key concepts from the set of documents, and these documents contain a vast amount of data. To find the key concepts from the data, we use the KNN algorithm.

Missing Data Imputation

Data sets frequently have missing values, which creates a problem for machine learning models or analysis. We need to replace the missing values before doing modeling or analysis. KNN is an effective algorithm for imputing the missing values in a process that’s called “nearest neighbor imputation.”

Learn More About Data ModelsExplaining 4 Important Data Processing Terms

Pattern Recognition

KNN is used to identify the patterns in text or images. For example, it is used to identify handwritten digit recognition, detect patterns in credit card usage and image recognition.

Banking

KNN is widely used in banking and financial use cases. In the banking sector, it helps to predict whether giving a loan to the customer is risky or safe. In financial institutes, it helps to predict the credit rating of customers.

K-Nearest Neighbor Pros

1. It’s simple to implement.
2. It’s flexible to different feature/distance choices.
3. It naturally handles multi-class cases.
4. It can do well in practice with enough representative data.

K-Nearest Neighbor Cons

1. We need to determine the value of parameter “K” (number of nearest neighbors).
2. Computation cost is quite high because we need to compute the distance of each query instance to all training samples.
3. It requires a large storage of data.
4. We must have a meaningful distance function.