L1 and L2 regularization are methods used to mitigate overfitting in machine learning models. These techniques are often applied when a model’s data set has a large number of features, and a less complex model is needed.
A regression model that uses the L1 regularization technique is called lasso regression, and a model that uses the L2 is called ridge regression.
L1 vs. L2 Regularization Methods
- L1 Regularization: Also called a lasso regression, adds the absolute value of the sum (“absolute value of magnitude”) of coefficients as a penalty term to the loss function.
- L2 Regularization: Also called a ridge regression, adds the squared sum (“squared magnitude”) of coefficients as the penalty term to the loss function.
Both L1 and L2 regularization add a penalty term to the loss function in a machine learning model. This puts weight on certain values to discourage the model from fitting training data too closely, and to reduce overall model complexity. However, both regularization methods have different penalty terms and specific use cases — here’s the key differences between them.
L1 Regularization: Lasso Regression
L1 regularization, or lasso (“least absolute shrinkage and selection operator”) regression, is a regularization method that penalizes high-value coefficients in a machine learning model. L1’s penalty term is the absolute value of the sum of coefficients (or the “absolute value of magnitude” of the coefficient), and is added to the model’s sum of squared errors (SSE) loss function.
Both penalty terms for L1 and L2 regularization are controlled by the model hyperparameter lambda (λ), which determines the tradeoffs between bias and variance in coefficients.
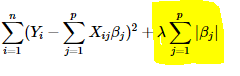
Lasso regression can reduce coefficient values to zero, enabling feature selection and removal. This aspect also allows lasso regression to handle some multicollinearity (high correlations among features) in a data set without affecting interpretability. However, lasso regression isn’t suitable for high multicollinearity — if there are highly-correlated covariates present, L1 regularization will randomly remove one of the features from the model.
Although it’s used to resolve overfitting, L1 regularization can actually cause model underfitting based on the lambda value. If lambda is zero, then regularization is disabled. Here, we’ll get back ordinary least squares (OLS) whereas a very large value will make coefficients zero. This means the model will become underfit.
L2 Regularization: Ridge Regression
L2 regularization, or ridge regression, is a regularization method that penalizes high-value coefficients in a machine learning model similarly to L1 regularization — though with a different penalty term. L2 regularization adds the squared sum of coefficients (or the “squared magnitude” of the coefficient) as the penalty term to the model’s SSE loss function.
Unlike L1 regularization, L2 regularization can reduce coefficient values toward zero but never exactly to zero. This also means that L2 regularization cannot perform feature selection.
The highlighted part below represents the L2 regularization element.
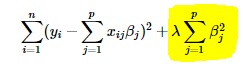
If model interpretability isn’t a concern, L2 regularization can effectively handle multicollinearity in a data set. Since ridge regression reduces coefficients close to zero, this helps to distribute the effects of correlated variables evenly across various features.
Again, if lambda is zero then you can imagine we get back OLS. However, if lambda is very large then it will add too much weight and lead to underfitting. Having said that, how we choose lambda is important. This technique works very well to avoid overfitting issues.
When to Use L1 vs. L2 Regularization
The key difference between L1 and L2 regularization techniques is that lasso regression shrinks the less important feature’s coefficient to zero, removing some features altogether. In other words, L1 regularization works well for feature selection in case we have a huge number of features.
Traditional methods like cross-validation and stepwise regression to perform feature selection and handle overfitting work well with a small set of features, but L1 and L2 regularization methods are a great alternative when you’re dealing with a large set of features.
Frequently Asked Questions
What is the L2 regularization?
L2 regularization, or ridge regression, is a machine learning regularization technique used to reduce overfitting in a machine learning model. L2 regularization’s penalty term is the squared sum of coefficients, and applies this into the model’s sum of squared errors (SSE) loss function to mitigate overfitting. L2 regularization can reduce coefficient values and feature weights toward zero (but never exactly to zero), so it cannot perform feature selection like L1 regularization.
Should I use L1 or L2 regularization?
L1 regularization is most effective for enabling feature selection and maintaining model interpretability, while L2 regularization is effective for handling multicollinearity and prioritizing model accuracy and stability.
How does L2 regularization prevent overfitting?
Both L2 regularization and L1 regularization prevent overfitting in machine learning models by applying penalty weights on values. This prevents models from putting too much importance on specific features, which encourages a more balanced weight distribution across all features and a generalized, less complex model.
What is the difference between L1 and L2 norm?
The L1 regularization norm is calculated as the sum of absolute values of the vector. The L2 regularization norm is calculated as the square root of the sum of the squared vector values.





