Logistic regression is a supervised machine learning algorithm widely used for classification. We use logistic regression to predict a binary outcome (1/0, Yes/No, True/False) given a set of independent variables. To represent binary/categorical outcomes, we use dummy variables.
What Is Logistic Regression?
Logistic regression is a statistical model that estimates the probability of a binary event occurring, such as yes/no or true/false, based on a given dataset of independent variables.
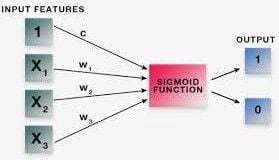
Logistic regression uses an equation as its representation, very much like linear regression. In fact, logistic regression isn’t much different from linear regression, except we fit a sigmoid function in the linear regression equation.
Simple linear and multiple linear regression equation:
y = b0 + b1x1 + b2x2 + ... + e
Sigmoid function:
p = 1 / (1 + e ^ -(y))
Logistic regression equation:
p = 1 / (1 + e ^ -(b0 + b1x1 + b2x2 +... + e))
In this case:
pis the probability of outcomeyis the predicted outputb0is the bias or intercept term
Each column in your input data has an associated b coefficient (a constant realvalue) that your training data must learn.
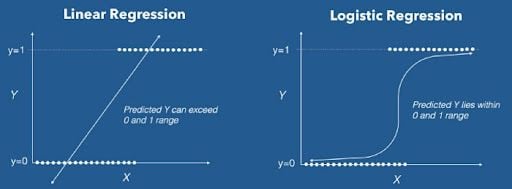
Linear Regression vs. Logistic Regression: What’s the Difference?
In linear regression the target is a continuous (real value) variable while in logistic regression, the target is a discrete (binary or ordinal) variable.
The predicted value in the case of linear regression is the mean of the target variable at the given values of the input variables. On the other hand, the predicted value in logistic regression is the probability of particular target variable level(s) at the given values of the input variables.
What Are the Advantages of Logistic Regression?
- No assumptions about distributions of classes in feature space
- Easily extend to multiple classes (multinomial regression)
- Natural probabilistic view of class predictions
- Quick to train and very fast at classifying unknown records
- Good accuracy for many simple data sets
- Resistant to overfitting
What Are the Disadvantages of Logistic Regression?
- Cannot handle continuous variables
- Won’t work If independent variables aren’t correlated with the target variable
- Require large sample sizes for stable results
Types of Logistic Regression
Binary Logistic Regression
The target variable has only two possible outcomes such as classifying emails as spam or not spam.
Multinomial Logistic Regression
The target variable has three or more categories without ordering, such as predicting what kind of food a group of people prefer more (vegetarian, non-vegetarian or vegan).
Ordinal Logistic Regression
The target variable has three or more categories with ordering, such as rating a movie from one to five.
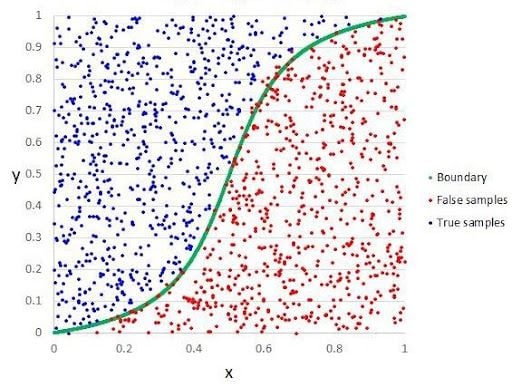
Decision Boundary in Logistic Regression
To predict the class to which data belongs, you can set a threshold which we call the decision boundary. Based upon this threshold, we classify the obtained estimated probability into different classes. Say, if predicted_value ≥ 0.5, then classify email as spam else as not spam.
Decision boundaries can be linear or nonlinear. You can also increase the polynomial order to get a complex decision boundary.
Logistic Regression Assumptions
- Binary logistic regression requires the dependent variable to be binary.
- Dependent variables are not measured on a ratio scale.
- You should only include meaningful variables.
- The independent variables should be independent of each other. That is, the model should have little or no multicollinearity.
- Logistic regression requires large sample sizes.
Frequently Asked Questions
What is logistic regression in simple terms?
Logistic regression is a statistical model that estimates how likely a binary outcome will occur, such as in yes/no or true/false scenarios, based on analyzing previous variable data.
Since logistic regression determines a probability, the dependent variable in this model will always be a value between 0 and 1.
What is the difference between linear regression and logistic regression?
Linear regression can model variable outcomes on a continuous scale, while logistic regression can only model variable outcomes on a discrete or categorical scale.
What is logistic regression best used for?
Logistic regression is best used for classification and prediction problems in machine learning. It can be applied to help identify fraud, determine disease likelihood or predict user behavior on websites and apps.





