An ensemble model is a machine learning model that combines multiple individual models to improve prediction accuracy, as opposed to using just one model alone.
What Are Ensemble Models?
Ensemble models are a machine learning approach that combine multiple individual models (known as base estimators) in the prediction process. Ensemble models offer a solution to overcome the technical challenges of building a single estimator.
Anytime we need to make an important decision, we try to collect as much information as possible and reach out to experts for advice. The more information we can gather, the more we (and those around us) trust the decision-making process.
Machine learning predictions follow a similar logic: Models process inputs and produce predictions based on patterns they learned during the training process. However, in many cases one model is not sufficient to achieve accurate results. This article explores this point, addressing key questions around when and why multiple models are necessary, how those models should be trained, and what kind of diversity they should provide. Let’s jump right in.
And if you want to see an example of how to build an ensemble model, you can skip to the end!
What Is an Ensemble Model?
An ensemble model is a group of two or more individual machine learning models that are combined to make more accurate predictions. In an ensemble model, several diverse models tend to be trained on the same task and have their predictions put together, creating a predictive model that is stronger than one machine learning model alone.
The individual models used in an ensemble are often called base estimators or base learners. In boosting, a special type of base learner is used, called a weak learner, which is a model that performs only slightly better than a random guess. A single, non-ensemble model is a single estimator.
Why Use an Ensemble Model?
Using an ensemble model approach often outperforms singular machine learning models or single estimators in prediction accuracy.
A single algorithm may not make the perfect prediction for a given data set. Machine learning algorithms have their limitations and producing a model with high accuracy is challenging. If we build and combine multiple models, we have the chance to boost the overall accuracy. We then implement the combination of models by aggregating the output from each model with two objectives:
- Reducing the model error
- Maintaining the model’s generalization
You can implement such aggregation using different techniques, sometimes referred to as meta-algorithms.
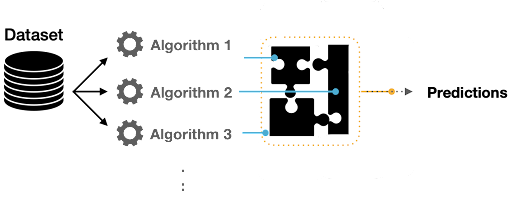
Applying an ensemble model can also help overcome the technical challenges of building a single estimator, which include:
- High variance: The model is very sensitive to the provided inputs for the learned features.
- Low accuracy: One model (or one algorithm) to fit the entire training data might not provide you with the nuance your project requires.
- Features noise and bias: The model relies heavily on too few features while making a prediction.
How Do Ensemble Models Work?
When we’re building ensemble models, we’re not only focusing on the algorithm’s variance. For instance, we could build multiple C45 models where each model is learning a specific pattern specialized in predicting any given thing. Models we can use to obtain a meta-model are called weak learners. In this ensemble learning architecture, the inputs are passed to each weak learner while also collecting their predictions. We can use the combined prediction to build a final ensemble model.
One important thing to mention is that weak learners can have different ways of mapping features with variant decision boundaries.
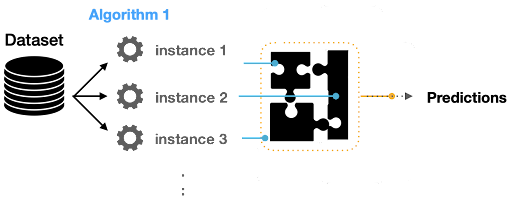
Aggregating Predictions
When we ensemble multiple algorithms to adapt the prediction process to combine multiple models, we need an aggregating method.
We can use three main techniques:
- Max Voting: The final prediction in this technique is made based on majority voting for classification problems.
- Averaging: This technique is typically used for regression problems where we average predictions. We can use the probability as well, for instance, by averaging the final classification.
- Weighted Average: Sometimes, we need to give weights to some models/algorithms when producing the final predictions.
Types of Ensemble Model Techniques
1. Bagging
Bagging (or bootstrap aggregation) is a parallel process, where it trains multiple models independently on different subsets of the data simultaneously. This method reduces variance and minimizes overfitting. A classic example of a bagging technique is the random forest algorithm.
Bagging is based on a bootstrapping sampling technique. Bootstrapping creates multiple sets of the original training data with replacement. Replacement enables the duplication of sample instances in a set. Each subset has the same equal size and can be used to train models in parallel.
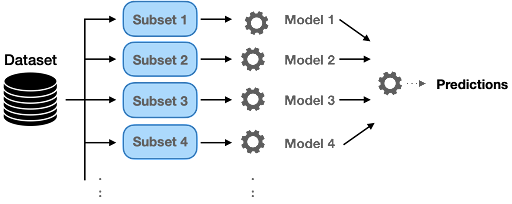
Random Forest
Random forest uses a subset of training samples as well as a subset of features to build multiple split trees. Multiple decision trees are built to fit each training set. The distribution of samples/features is typically implemented in a random mode.
Extra-Trees Ensemble
Extra-trees ensemble is another ensemble technique where the predictions are combined from many decision trees. Similar to random forest, it combines a large number of decision trees. However, the extra trees use the whole sample while choosing the splits randomly.
2. Boosting
Adaptive Boosting (AdaBoost)
Adaptive boosting (AdaBoost) is an ensemble of algorithms, where we build models on the top of several weak learners . As we mentioned earlier, those learners are called weak because they are typically simple with limited prediction capabilities. The adaptation capability of AdaBoost made this technique one of the earliest successful binary classifiers.
Sequential Decision Trees
These were the core of such adaptability where each tree adjusts its weights based on prior knowledge of accuracies. Hence, we perform the training in such a technique in a sequential (rather than parallel) process. In this technique, the process of training and measuring the error in estimates can be repeated for a given number of iterations or when the error rate is not changing significantly.

Gradient Boosting
Gradient boosting algorithms are great techniques that have high predictive performance. XGBoost, LightGBM and CatBoost are popular boosting algorithms you can use for regression and classification problems.
3. Stacking
Stacking is similar to boosting models; they produce more robust predictors. Stacking is a process of learning how to create such a stronger model from all weak learners’ predictions.

Please note that the algorithm is learning the prediction from each model (as features).
4. Blending
Blending is similar to stacking, but it uses a holdout validation set to train the final meta-model. This prevents the meta-model from being trained on data it's supposed to evaluate. The base models make predictions on the validation set, and these predictions serve as the features for the final model.
What Tasks Are Ensemble Models Used For?
Classification Problems
Classification is simply a categorization process. If we have multiple labels, we need to decide: Shall we build a single multi-label classifier? Or shall we perhaps build multiple binary classifiers? If we decide to build a number of binary classifiers, we need to interpret each model prediction. For instance, if we want to recognize four objects, each model tells you if the input data is a member of that category. Hence, each model provides a probability of membership. Similarly, we can build a final ensemble model combining those classifiers.
Regression Problems
In the previous function, we determined the best fitting membership using the resulting probability. In regression problems, we are not dealing with “yes” or “no” questions. Instead, we need to find the best predicted numerical values and then we can average the collected predictions.
How to Build an Ensemble Model: An Example
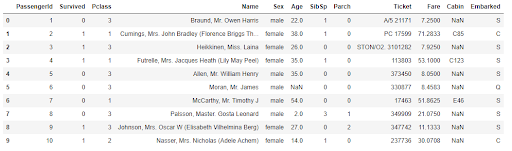
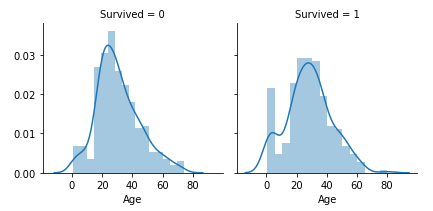
We’ll use the following example to illustrate how to build an ensemble model. We’ll use the Titanic data set and try to predict the survival of the Titanic using different techniques. A sample of the data set and the target column distribution to the passengers’ age are shown in figures six and figure seven. If you want to follow along you can find the sample code on my GitHub.
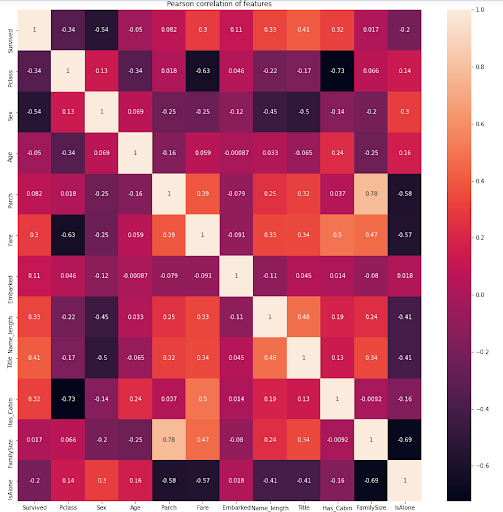
The Titanic data set is one of the classification problems that needs extensive feature engineering. Figure eight below shows the strong correlation between some features such as Parch (parents and children) with the Family Size. We will try to focus only on the model building and how the ensemble model can be applied to this use case.
We will use different algorithms and techniques; therefore, we will create a model object to increase code reusability.
# Model Class to be used for different ML algorithms
class ClassifierModel(object):
def __init__(self, clf, params=None):
self.clf = clf(**params)
def train(self, x_train, y_train):
self.clf.fit(x_train, y_train)
def fit(self,x,y):
return self.clf.fit(x,y)
def feature_importances(self,x,y):
return self.clf.fit(x,y).feature_importances_
def predict(self, x):
return self.clf.predict(x)
def trainModel(model, x_train, y_train, x_test, n_folds, seed):
cv = KFold(n_splits= n_folds, random_state=seed)
scores = cross_val_score(model.clf, x_train, y_train, scoring='accuracy', cv=cv, n_jobs=-1)
return scoresRandom Forest Classifier
# Random Forest parameters
rf_params = {
'n_estimators': 400,
'max_depth': 5,
'min_samples_leaf': 3,
'max_features' : 'sqrt',
}
rfc_model = ClassifierModel(clf=RandomForestClassifier, params=rf_params)
rfc_scores = trainModel(rfc_model,x_train, y_train, x_test, 5, 0)
rfc_scoresExtra Trees Classifier
# Extra Trees Parameters
et_params = {
'n_jobs': -1,
'n_estimators':400,
'max_depth': 5,
'min_samples_leaf': 2,
}
etc_model = ClassifierModel(clf=ExtraTreesClassifier, params=et_params)
etc_scores = trainModel(etc_model,x_train, y_train, x_test, 5, 0) # Random Forest
etc_scoresAdaBoost Classifier
# AdaBoost parameters
ada_params = {
'n_estimators': 400,
'learning_rate' : 0.65
}
ada_model = ClassifierModel(clf=AdaBoostClassifier, params=ada_params)
ada_scores = trainModel(ada_model,x_train, y_train, x_test, 5, 0) # Random Forest
ada_scoresXGBoost Classifier
# Gradient Boosting parameters
gb_params = {
'n_estimators': 400,
'max_depth': 6,
}
gbc_model = ClassifierModel(clf=GradientBoostingClassifier, params=gb_params)
gbc_scores = trainModel(gbc_model,x_train, y_train, x_test, 5, 0) # Random Forest
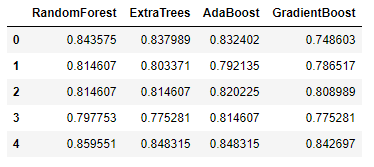
gbc_scoresLet’s combine all the model cross-validation accuracy on five folds.
Now let’s build a stacking model where a new stronger model learns the predictions from all these weak learners. Our label vector used to train the previous models will remain the same. The features are the predictions collected from each classifier.
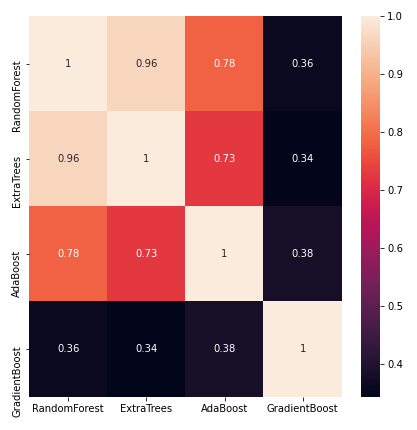
x_train = np.column_stack(( etc_train_pred, rfc_train_pred, ada_train_pred, gbc_train_pred, svc_train_pred))Now let’s see if building an XGBoost model learning only the resulting prediction will perform better. But first, we will take a quick peek at the correlations between the classifiers’ predictions.
We’ll now build a model to combine the predictions from multiple contributing classifiers.
def trainStackModel(x_train, y_train, x_test, n_folds, seed):
cv = KFold(n_splits= n_folds, random_state=seed)
gbm = xgb.XGBClassifier(
n_estimators= 2000,
max_depth= 4,
min_child_weight= 2,
gamma=0.9,
subsample=0.8,
colsample_bytree=0.8,
objective= 'binary:logistic',
scale_pos_weight=1).fit(x_train, y_train)
scores = cross_val_score(gbm, x_train, y_train, scoring='accuracy', cv=cv)
return scoresThe previously created base classifiers represent Level-0 models, and the new XGBoost model represents the Level-1 model. The combination illustrates a meta-model trained on the predictions of sample data. You can see a quick comparison between the accuracy of the new stacking model and the base classifiers below:
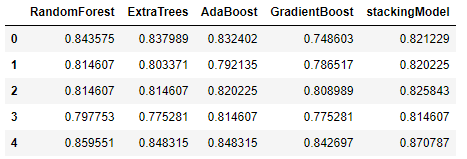
Ensemble Model Considerations
- Noise, bias and variance: The combination of decisions from multiple models can help improve the overall performance. Hence, one of the key reasons to use ensemble models is overcoming noise, bias and variance. If the ensemble model does not give the collective experience to improve upon the accuracy in such a situation, then it’s necessary to carefully rethink if such employment is necessary.
- Simplicity and explainability: Machine learning models, especially those put into production environments, should be simple to explain. The chances you’ll be able to explain the final model decision is drastically reduced when you’re using an ensemble model.
- Generalizations: Ensemble models, particularly boosting methods, can be prone to overfitting if not trained carefully. Because these models are designed to correct the errors of previous models, they can end up memorizing the training data, which hurts their ability to generalize to new, unseen data.
- Inference time: Although we might be resigned to accept a longer time for model training, inference time is still critical. When deploying ensemble models into production, the amount of time needed to pass multiple models increases and could slow down the prediction tasks’ throughput.
Ensemble models are an excellent method for machine learning because they offer a variety of techniques for classification and regression problems. Now you know the types of ensemble models, how we can build a simple ensemble model and how they boost the model accuracy.
Frequently Asked Questions
What is an ensemble model?
An ensemble model is a machine learning model that combines multiple individual learning models (known as base estimators) together to help make more accurate predictions. Ensemble models tend to work by training its base estimators on a similar task, and combining their predictions to increase accuracy in comparison to using only one machine learning model.
What are the types of ensemble models?
The main types of ensemble learning techniques used for ensemble models are:
- Bagging
- Boosting
- Stacking
- Blending
What is ensemble learning?
Ensemble learning is a machine learning technique that describes the use of ensemble models, where multiple individual learning models are combined to improve prediction accuracy.





