Bootstrapping is a statistical resampling technique that uses repeated sampling from a single data set to generate simulated samples for estimating measures like variability, confidence intervals and bias.
Bootstrapping Statistics Defined
Bootstrapping is a statistical resampling method that uses repeated sampling with replacement from a single data set to estimate statistics such as standard errors, confidence intervals and bias. It can also be applied to hypothesis testing. The bootstrapping approach allows you to approximate the sampling distribution and calculate statistics from a small data set without collecting new samples.
Most of the time when you’re conducting statistical research, it’s impractical to collect data from the entire population. This can be due to budget and/or time constraints, among other factors. Instead, a subset of the population is taken and insight is gathered from that subset to learn more about the population.
This means that suitably accurate information can be obtained quickly and relatively inexpensively from an appropriately drawn sample. However, many things can affect how well a sample reflects the population, and therefore, the validity and reliability of the conclusions. Because of this, let us talk about bootstrapping statistics.
What Is Bootstrapping Statistics?
“Bootstrapping is a statistical procedure that resamples a single data set to create many simulated samples. This process allows for the calculation of standard errors, confidence intervals, and hypothesis testing,” according to a post on bootstrapping statistics from statistician Jim Frost.
Bootstrapping is a simple yet powerful alternative to traditional hypothesis testing, helping address some of its limitations.
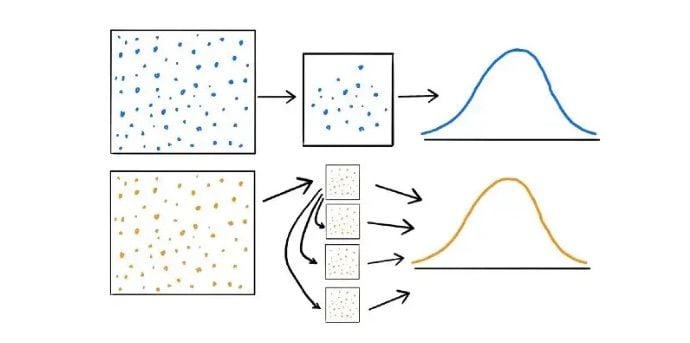
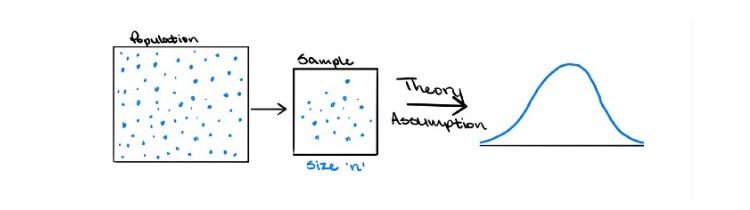
In traditional statistical inference, estimates about a population are typically drawn from a single sample of size n, with results generalized using the sampling distribution and standard error of the statistic of interest. This distribution represents all possible estimates if the population were repeatedly sampled.
Under the Central Limit Theorem, and if certain conditions are met, the sampling distribution of the mean approaches normality as the sample size grows. However, skewed or heavy-tailed data may require much larger samples for this approximation to hold. When the sample size is too small, the normality assumption may not apply, making it harder to estimate the standard error and draw reliable conclusions.
Bootsrapping aims to mitigate the above issue.
How Bootstrapping Statistics Works
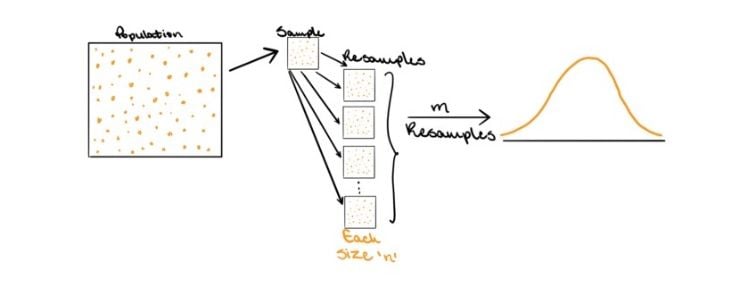
In the bootstrapping approach, a sample of size n is drawn from the population. Let’s call this sample S. Then, rather than using theory to determine all possible estimates, the sampling distribution is created by resampling observations with replacement from S m times, with each resampled set having n observations.
Now, if sampled appropriately, S should be representative of the population. Therefore, by resampling S m times with replacement, it would be as if m samples were drawn from the original population, and the estimates derived would be representative of the theoretical distribution under the traditional approach.
Increasing the number of resamples, m, will not increase the amount of information in the data. That is, resampling the original set 100,000 times is not more useful than resampling it 1,000 times. The amount of information within the set is dependent on the sample size, n, which will remain constant throughout each resample. The benefit of more resamples, then, is to derive a better estimate of the sampling distribution.
Resampling in Bootstrapping Statistics
Resampling is the process of taking a sample and using it to produce simulated samples for more accurate calculations. To better understand what this means, consider these basic principles:
- Each data point in the original sample has an equal chance of being chosen and resampled into a simulated sample.
- Because data points are returned to the original sample after being selected, a data point may be chosen more than once for the same simulated sample.
- Each resampled, or simulated, sample is the same size as the original sample.
Keep in mind that it’s often best to create at least 1,000 simulated samples for bootstrapping to work properly.
Applications of Bootstrapping Statistics
Training Machine Learning Algorithms
In machine learning, bootstrapping is used to create multiple training or evaluation data sets from an original sample. This helps estimate model performance variability and can improve accuracy when combined in ensemble methods like bagging.
Testing Hypotheses
Traditional statistical methods often try to make generalizations about a data set based on a single sample. By gleaning insights from thousands of simulated samples, the bootstrapping method makes it possible to determine more accurate calculations.
Creating Confidence Intervals
When calculating a statistic of interest, bootstrapping can generate thousands of simulated samples that each feature their own statistic of interest. Teams can then develop a confidence interval that is more precise since it relies on a larger collection of samples as opposed to just one sample or a few samples.
Calculating Standard Error
Bootstrapping is more equipped than traditional methods for calculating standard error since it generates many simulated samples at random. This makes it easier to determine the means of different samples and estimate a sampling distribution that is more reflective of the larger data set and can be used to find the standard error.
Advantages of Bootstrapping Statistics
“The advantages of bootstrapping are that it is a straightforward way to derive the estimates of standard errors and confidence intervals, and it is convenient since it avoids the cost of repeating the experiment to get other groups of sampled data. Although it is impossible to know the true confidence interval for most problems, bootstrapping is asymptotically consistent and more accurate than using the standard intervals obtained using sample variance and the assumption of normality,” according to author Graysen Cline in their book, Nonparametric Statistical Methods Using R.
Works With Multiple Types of Data
The bootstrapping approach works with many types of data because it does not require assuming a specific underlying distribution. Its accuracy, however, depends on the quality and representativeness of the original sample. In many cases, bootstrap estimates resemble those from traditional methods, but with small samples or non-normal data, bootstrapping can be more reliable.
Does Not Assume Normality and Is Less Dependent on Theoretical Assumptions
Unlike traditional methods, which often assume normality and depend on theoretical sampling distributions, bootstrapping builds its sampling distribution directly by resampling the observed data. This makes it less dependent on theoretical assumptions, though it still relies on the integrity of the initial sample. Outliers can influence results in both bootstrapping and traditional approaches; in bootstrapping, repeated resampling may amplify their impact, while in traditional methods they can inflate the mean and standard error.
Flexible and Useful When Traditional Assumptions Aren’t Met
Both bootstrapping and traditional methods require appropriately drawn samples to make valid inferences. The key difference lies in mechanics: traditional methods use theory to model the sampling distribution, which can fail if assumptions aren’t met, while bootstrapping observes the distribution empirically through resampling. This allows for flexible and accurate estimation of statistics, especially when theoretical models are unreliable.
Limitations of Bootstrapping Statistics
Bootstrapping offers many benefits compared to traditional statistical methods, but there are some downsides to consider:
- Time-consuming: Thousands of simulated samples are needed for bootstrapping to be accurate.
- Computationally taxing: Because bootstrapping requires thousands of samples and takes longer to complete, it also demands higher levels of computational power.
- Incompatible at times: Bootstrapping isn’t always the best fit for a situation, especially when dealing with spatial data or a time series.
- Prone to bias: Bootstrap estimates can be biased if the original sample is unrepresentative or if the statistic of interest has a highly skewed sampling distribution.
Frequently Asked Questions
What is the purpose of bootstrapping statistics?
The purpose of bootstrapping is to estimate the sampling distribution of a statistic from limited data, enabling calculations such as standard errors, confidence intervals and hypothesis tests without relying on strict distributional assumptions.
What is the difference between bootstrapping and traditional statistical methods?
Bootstrapping takes one sample and repeatedly resamples it to create many simulated samples, using their sampling distribution to make inferences about the population. Traditional statistical methods typically use one sample and rely on theoretical assumptions about its sampling distribution to estimate population parameters.
What is a good sample size for bootstrapping?
Many practitioners use at least 1,000 simulated samples, but the optimal number depends on the desired precision and available computing power.
What is the difference between bootstrapping and sampling?
Bootstrapping involves resampling an existing sample to create multiple new simulated samples of a population. Sampling traditionally involves only taking one sample (or smaller group of data) from a larger population, and can be performed in different types of ways (simple random sampling, cluster sampling, etc.).





