The Difference Between Standard Deviation and Standard Error

Have you ever wondered what the difference is between standard deviation and standard error?

If you haven’t, here’s why you should care. 

What Is Standard Deviation?

Standard deviation measures the dispersion — variability — of the data in relation to the mean. In other words, the closer to zero the standard deviation is, the closer to the mean the values are in the studied data set. A normal distribution gives us valuable information in terms of the percentage of data within one, two and three standard deviations from the mean.

Let’s use R to generate some random data:

#generating some random data
set.seed(20151204)
#computing the standard deviation
x<-rnorm(10)
sd(x)
# result: 1.14415

Now, let’s generate a normally distributed graph:

#generating the normally distributed graph with description of segments
plot(seq(-3.2,3.2,length=50),dnorm(seq(-3,3,length=50),0,1),type="l",xlab="",ylab="",ylim=c(0,0.5))
segments(x0 = c(-3,3),y0 = c(-1,-1),x1 = c(-3,3),y1=c(1,1))
text(x=0,y=0.45,labels = expression("99.7% of the data within 3" ~ sigma))
arrows(x0=c(-2,2),y0=c(0.45,0.45),x1=c(-3,3),y1=c(0.45,0.45))
segments(x0 = c(-2,2),y0 = c(-1,-1),x1 = c(-2,2),y1=c(0.4,0.4))
text(x=0,y=0.3,labels = expression("95% of the data within 2" ~ sigma))
arrows(x0=c(-1.5,1.5),y0=c(0.3,0.3),x1=c(-2,2),y1=c(0.3,0.3))
segments(x0 = c(-1,1),y0 = c(-1,-1),x1 = c(-1,1),y1=c(0.25,0.25))
text(x=0,y=0.15,labels = expression("68% of the data within 1" * sigma),cex=0.9)

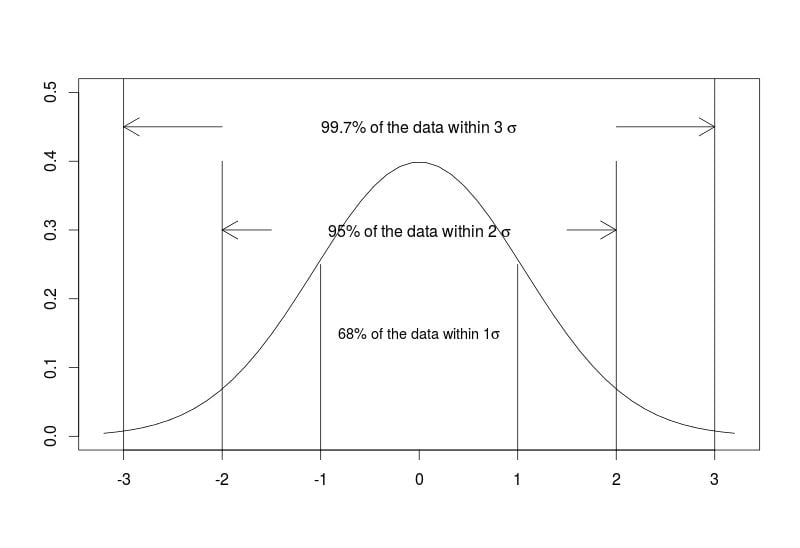
When we calculate the mean of a particular sample, we want to draw conclusions about the larger population from which the sample comes. We usually collect representative sample data because we’re limited in terms of resources for collecting information about the whole population. So, we’ll use it as an estimate of the whole population mean.

More on DataWhat Is a Boxplot? Definition and How to Use One.

What Is Standard Error?

Of course, there will be different means for different samples from the same population. The standard deviation of these various sample means is the standard error. In short, standard error measures the precision of the estimate of the sample mean.

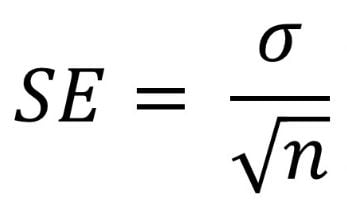
The standard error is strictly dependent on the sample size. As a result, the standard error falls as the sample size increases. If you think about it, the bigger the sample, the closer the sample mean is to the population mean, so the closer the estimate is to the actual value.

R code for computing standard error below:

#computation of the standard error of the mean
sem<-sd(x)/sqrt(length(x))

More on Data20 Data Modeling Tools You Should Know

Standard Deviation vs. Standard Error

If you need to draw conclusions about the spread and variability of the data, use standard deviation.

If you’re interested in finding how precise the sample mean is or you’re testing the differences between two means, then standard error is your metric.

Frequently Asked Questions