Beam search is an approximate search algorithm commonly used in natural language processing, although its potential applications are very wide. It balances time and memory usage with the quality of its final answer. It does so by only ever keeping the top k solution candidates in memory at a time and choosing the best result found at the end of the search. Let’s look at the details.
What is the Beam Search Algorithm?
Beam search is an approximate search algorithm commonly used in natural language processing. It is applicable to any problem that involves search, which gives it broad applicability. It balances time and memory usage with the quality of its final answer by only ever keeping the top k solution candidates in memory at a time and choosing the best result found at the end of the search.
Beam Search Algorithm Fundamentals
At a high level, beginning from the start state in some search space, we generate all possible successor states and keep only the “best” k candidates. We then generate all the successors for those k states, again keep just the top k among these options, and so on. When the search is over, we go with the best solution found so far.
This is essentially a variant of breadth-first search (BFS), except after we expand all the frontier nodes, instead of keeping every successor state in the frontier, we only keep the best k. This generates k “beams” that carve through search space, as visualized below with k = 3:
This leaves open two questions: how do we decide which states are “best,” and when does the algorithm terminate?
We’ll need some kind of evaluation function for states. If we’re searching for a final goal state, this function could be a heuristic that estimates how close we are to the goal. In path planning, for example, it could estimate the distance to the destination.
Other functions try to measure the overall quality of a state in a more objective sense. A chess program could weigh up the material in a board state, for instance. A particularly interesting special case is when we’re trying to find some state of highest probability and our scoring function estimates how likely a state is. This example is used in text generation to search for a high-probability word sequence.
Beam search has many possible terminating conditions. Perhaps the simplest is to halt as soon as you’ve reached a terminal or goal state. But not all problems have predefined states like this, and even if they do, you may want to keep searching to find a better path to the goal. You might instead halt once you reach a certain maximum search depth. Another common solution is to halt when it looks like the quality of states is no longer improving significantly, using some heuristic method.
Whatever the case, once the algorithm has halted, you’ll be left with the best k states the algorithm could find, and you can use your evaluation function to choose between them to get your final answer.
Application of the Beam Search Algorithm in Software Engineering
You can apply this algorithm to any problem that uses search, which covers a lot of ground. Any path planning system can use beam search, be it a robot navigating in a real-world environment, an AI navigating in a virtual environment, or a maps app searching for the best route.
Game-playing Systems
Game-playing systems can use beam search to look for the best moves, whether in chess, backgammon, or any other turn-based game. Beam search has even been used in circuit design to search for the best transistor layout on a chip.
Language Models
Perhaps the most significant use of beam search, however, is in natural language processing. Language models (LMs) assign probabilities to words and sequences of words. In particular, they’re often used for next-word prediction, which involves guessing which single word should come next given all the words before it. You can repeat this process to generate whole sentences or more.
We can use search to enhance this process. Instead of considering probabilities one word at a time, we can search over whole sequences to find the most likely one. Doing so can enhance LM output by improving its overall coherency and consistency. Of course, to do a full search over all possible word sequences would be intractable. Instead, we can apply beam search to produce a high-quality output in a reasonable amount of time.
Advantages of Beam Search Algorithm
Beam search offers several advantages.
Saves Time and Memory
Compared to exhaustive search, beam search uses significantly less time and memory. It’s a highly scalable method: Even as we increase the size of the search space, the amount of information we keep in memory and process at any given time remains constant.
Effective Sharing Between Branches
Beam search also has the advantage of effectively sharing information between branches; we can abandon one branch if we see a promising solution on another. Running beam search with k beams is thus typically more effective than running k separate searches. Relatedly, beam search is highly parallelizable. We can run the different beams in parallel on separate processors, significantly speeding up the search.
Configurable Beam Width
One last advantage is that the beam width k is configurable. Thus, we can easily tune the time and memory budget we wish to dedicate to the search process. Since we only ever have k solutions in memory at a time, we can increase k if we have a lot of memory available and decrease it if we have little.
Potential Limitations of Beam Search Algorithm
Beam search does have some potential disadvantages, however.
Incomplete Algorithm
First, it’s an incomplete algorithm, meaning it’s not guaranteed to find the best solution, or indeed any solution. It abandons certain branches in the search space when they no longer look promising, and if such branches were in fact the only paths to the optimal solution, then it will never be able to find said solution.
Stuck at Local Optima
Relatedly, beam search can get stuck at local optima. The algorithm may find itself in a state where any local change makes the solution worse, and only a relatively long series of steps will make it better. If each intermediate step looks bad to our heuristic evaluation function, then beam search will not explore such paths.
Diversity Among Beams
Another significant issue is diversity among the beams. Ideally, we want our k branches to consider k distinct solutions in order to maximize exploration. Often, however, the branches will actually converge to k states that are all very similar to each other. If this happens, we pay the expense of maintaining k branches but effectively only gain the benefits of one.
Solutions
We do have ways of addressing these problems, though. For example, we can select successor states randomly rather than deterministically — favoring higher-scoring states, of course — to encourage exploration. Additionally, we can include a penalty for candidate states that are too similar to those we’ve already included. This latter idea requires some measure of state similarity. That is, if we are to eliminate states that are “too similar” to the current set, then we need some function that computes how similar two states are.
Use Cases of Beam Search Algorithm With Examples
To finish, let’s walk through an example of how to use beam search for text generation, inspired by Speech and Language Processing (Jurafsky & Martin, 2023, Sec. 10.4). Suppose we have a very small vocabulary, consisting of just the words “ok” and “yes,” as well as an end-of-sequence token “</s>,” which indicates that we should stop generating output. Here’s a possible search tree:
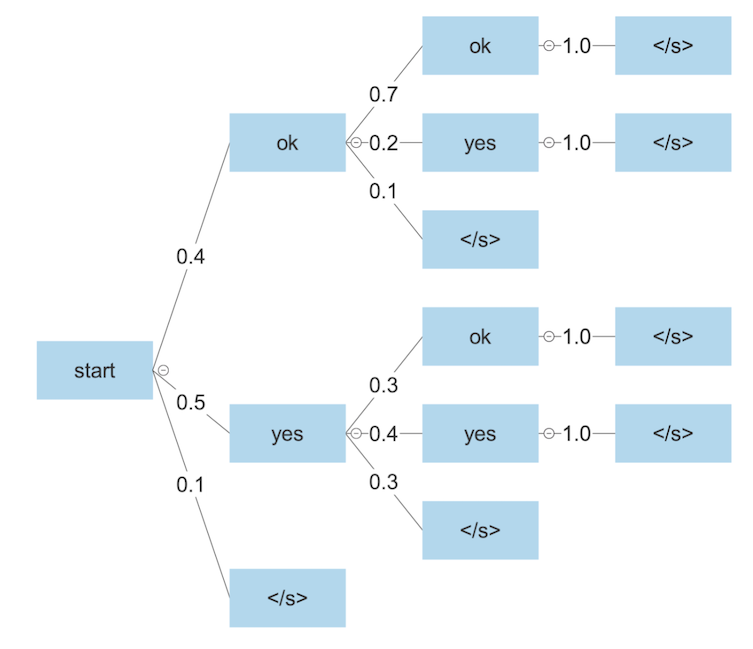
The edges indicated probabilities of generating the next token, given all the previous, as estimated by our language model. We want to search through this tree to find the most probable sequence.
Suppose we perform a beam search with k=2. Beginning from the start node, we generate all three successor states and compute their probabilities, getting “ok” (0.4), “yes” (0.5), and “</s>” (0.1). We keep just the top two, “ok” and “yes.”
Next, we generate all successor states for both of them and once again compute the probabilities. We get “ok ok” (0.4 * 0.7 = 0.28), “ok yes” (0.4 * 0.2 = 0.08), “ok </s>” (0.4 * 0.1 = 0.04), “yes ok” (0.5 * 0.3 = 0.15), “yes yes” (0.5 * 0.4 = 0.2), and “yes </s>” (0.5 * 0.3 = 0.15). Thus the top two are “ok ok” and “yes yes.”
Finally, both these states have just one successor state which they are guaranteed to go to: “</s>.” So, our final two answers are “ok ok </s>” (0.28) and “yes yes </s>” (0.2). We thus output “ok ok </s>” since it has the highest probability. This also happens to be the optimal choice in the whole search tree!
You may notice that our probabilities decrease as we search deeper in the tree since we successively multiply probabilities together. This often causes us to favor short sequences over long ones, which may not be desirable. It didn’t come up in this example, because the end-of-sequence token never looked like a good option until the end. But if we’d chosen it as one of our k states earlier on, then as we continued expanding the other k - 1, they would become less and less probable in comparison.
To avoid this problem, we often normalize the probability of a state based on its corresponding sequence length. To accomplish this, we first take the log of each probability, which is fairly standard in machine learning. Then we divide by the length of the sequence. We thus search for the sequence with the highest average log probability, which significantly reduces the penalty for long answers.
And there you have it! If you’d like to learn about other text generation strategies, you can try looking at HuggingFace’s documentation here. They also have a lot of models to get started with. Have fun!
