Binary is a numerical system that uses only two digits, 0 and 1, to represent values. You’ll sometimes see this referred to as a base-2 system. Binary differs from the decimal system that we use every day, which uses ten digits (0-9) to represent values — also called the base-10 number system. While decimal is better suited for human comprehension, binary is more efficient for computers.
Why Is Binary Important?
Binary plays a critical role in computing because it allows computers to store and manipulate data using a system of switches that can be turned on or off, represented by the digits 0 and 1. This binary code can represent any type of data, from text and numbers to images and sound. Without binary, it would be impossible for computers to communicate, perform calculations or store information.
Binary may seem intimidating at first, especially for those without a background in computer science or mathematics. However, with a little bit practice, anyone can understand how binary works and why it’s important.
How Do Binary Numbers Work?
In binary, each digit is referred to as a bit, which is short for binary digit. The value of each bit depends on its position within a number, with the rightmost bit representing the ones place, the next bit to the left representing the twos place and so on. Each bit can either be 0 or 1, which corresponds to the absence or presence of an electrical charge in a computer’s memory or storage device.
Binary vs. Decimal
Decimal is the number system with which most people are familiar. It uses ten digits (0-9) to represent values and is also known as the base-10 number system. In contrast, binary uses only two digits (0 and 1) — also known as base-2. While the decimal system is better suited for human comprehension, binary is more efficient for computers since it requires fewer switches — that is, commands to interpret — in order to represent the same value.
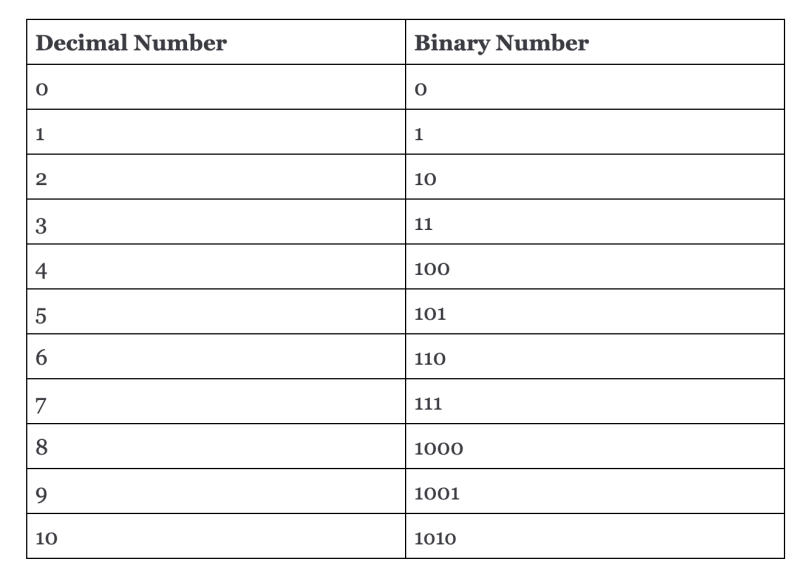
Representing Decimals in Binary Format
To convert a decimal number into binary, we repeatedly divide the number by two until the result is 0. The remainder of each division is recorded as a binary digit (bit), with the least significant bit being the rightmost digit. For example, the decimal number 10 in binary format is 1010. To reach this conclusion we can perform the following computation:
(1x23 + 0x22 + 1x21 + 0x20)
If you take the same logic, you’ll see that 1111 in binary is 15 in decimal. (1x23 + 1x22 + 1x21 + 1x20)
1100100 is 100. (1x27 + 1x26 + 0x25 + 0x24 + 1x23 + 0x22 + 0x21)
11111111 is 255. (1x28 +1x27 + 1x26 + 1x25 + 1x24 + 1x23 + 1x22 + 1x21)
This one is particularly important because it’s the maximum number for a byte.
How to Convert Binary Numbers Into Text
Converting binary numbers into text involves translating each group of eight bits, known as a byte, into a corresponding character using a standard encoding such as ASCII (American Standard Code for Information Interchange). Each byte can represent up to 256 different characters, including letters, numbers and symbols.
This is why 11111111 = 255, and if you add 0, you get to 256, enough to represent any character you need in ASCII.
For example, if you wanted to spell “Hello World” in binary, you would end up with this:
01001000 01100101 01101100 01101100 01101111 00100000 01010111 01101111 01110010 01101100 01100100
Applications of Binary
We use binary in a wide range of applications including computer networking, digital communication, encryption and image processing. When you send an email, the message is broken down into binary code and transmitted across a network of switches and routers. Similarly, when you download a photo, the image is encoded as a series of binary digits that can be decoded and displayed on your screen.
Here are some common examples of how we use binary every day.
Computer Processors
Computer processors use binary to perform arithmetic and logical operations. When you add two numbers on a calculator, the calculator converts the numbers to binary, performs the addition using binary logic and then converts the result back to decimal.
File Compression and Decompression
We use binary in file compression and decompression. Compression algorithms like gzip and zip use binary code to represent the data in a more compact form, thereby reducing the amount of storage space required.
Cryptography
We use binary in cryptography to encode and decode messages. Cryptographic algorithms use binary code to perform operations like encryption, decryption and authentication. For example, the Advanced Encryption Standard (AES) uses binary code to encrypt and decrypt data securely.
Digital Audio and Video Processing
We use binary in digital audio and video processing. Audio and video files are encoded as streams of binary data, which are then decoded and converted back into analog signals for playback on speakers or screens.
Machine Learning and AI
We use binary in machine learning and artificial intelligence. For example, neural networks, which are used to recognize patterns in data and perform tasks like image recognition and language translation, operate using binary to represent the weights and connections between neurons.
