Big O, Big Theta and Big Omega notations express how an algorithm’s time and space complexity scales with input size. These notations help developers quantify and compare performance in worst, best and bounded scenarios.
Big O vs. Big Theta vs. Big Omega Explained
- Big O (
O): Represents the worst-case performance of an algorithm, setting an upper bound on growth. Example:O(n²). - Big Theta (
Θ): Represents a tight bound, where the algorithm’s growth rate is bounded above and below by the same function. Example:Θ(n). - Big Omega (
Ω): Represents the best-case performance, setting a lower bound on growth. Example:Ω(n).
While it can be a dry subject, understanding how Big O and the other notations work is important for technical interviews. So, to make it more fun, we’ll unravel the mysteries using the universal language of emojis.
Buckle up for a roller coaster of fun, knowledge and a few emojis along the way!
What Is Big O Notation?
Big O notation (O) describes the upper bound of an algorithm’s performance — how slowly it could run in the worst-case scenario as input size increases.
Imagine you’re delivering pizzas (🍕) to a number of parties (🎉), each with one guest (n or 👩💻). In the worst case, every guest is at a separate location, requiring a unique delivery.
This results in a quadratic number of operations: O(n²).
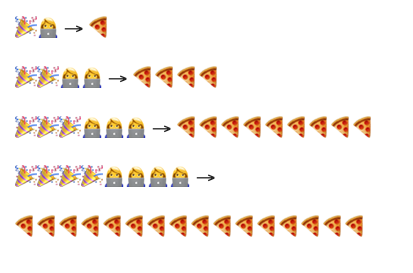
As both the number of guests and parties increases — and each delivery must be made separately — the time required grows proportionally to n².
What Is Big Theta Notation?
Big Theta (Θ) notation represents a tight bound on an algorithm’s performance — meaning the algorithm’s growth rate is bounded both above and below by the same function. In other words, its time or space complexity grows at the same rate in both best- and worst-case scenarios.
Let’s stick with the pizza delivery example (🍕). If the number of parties (🎉) is fixed, and the number of guests (n or 👩💻) increases, the time scales linearly — resulting in Θ(n).
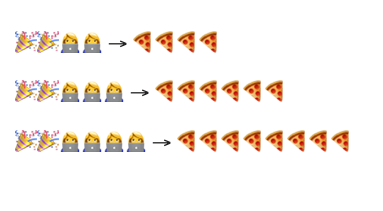
In contrast, if each guest is at a separate location, and each requires an individual delivery, the worst-case performance becomes O(n²).
Big Theta only applies when the algorithm’s upper and lower bounds match, reflecting consistent scaling behavior across all inputs.
What Is Big Omega Notation?
If all the guests are at the same party, Big Omega (Ω) describes the best-case scenario, where performance scales linearly with the number of guests (n): Ω(n).
Since the number of delivery locations is fixed at one, there’s no travel between parties — only the effort of baking and serving increases with n.
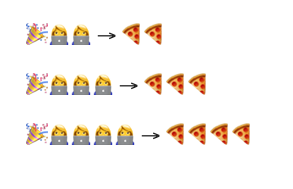
While parallel baking (e.g., using two ovens) might reduce real-world time, asymptotic notation ignores constant factors — so Ω(½n) is still written as Ω(n).
When to Use Big O vs. Big Theta
So, how do you choose between Big O and Big Theta (Θ) notations? It depends on the context.
When to Use Big O Notation
Use Big O notation to analyze the worst-case performance of an algorithm, which is critical for understanding potential bottlenecks under heavy load.
For Big O, think of the Diablo 4 beta weekend in which millions of users simultaneously tried to play at the same time.
When to Use Big Theta Notation
Use Big Theta notation when you can prove that an algorithm’s upper and lower bounds match, showing consistent growth across inputs.
For performance analysis, you might care about both worst-case behavior (Big O) and how the algorithm performs on average inputs (average-case complexity). Percentiles like P50 or P99 are useful in benchmarking but don’t map directly to Big O or Big Theta, which are theoretical bounds.
Big O vs. Big Theta vs. Big Omega Tips
Here’s a fun emoji summary to help you remember the three measures of algorithmic complexity:

You can also remember the difference between Big O, Big Omega and Big Theta with this mnemonic:
- Big O (
O) is the worst case; it represents a one-sided upper bound, describing the maximum time or space an algorithm may require. - Big Theta (
Θ) is the average case; it represents a two-sided bound, meaning the algorithm’s growth is tightly bound from above and below by the same function. - Big Omega (
Ω) is the best case; it represents a one-sided lower bound, defining the minimum performance an algorithm can achieve under ideal conditions.
And there you have it. We’ve delved into the world of algorithmic complexity and explored the differences between Big O, Big Theta and Big Omega notations.
These notations allow developers to analyze how algorithms scale, compare different solutions, and make informed decisions when optimizing for speed or resource usage. Whether you’re developing a new app, building a website, or creating a game, understanding algorithmic complexity is a valuable skill.
So, next time you’re at a party, remember the pizza delivery (🍕) and how algorithmic complexity can help you ace your next technical interview.
Frequently Asked Questions
What is Big O notation?
Big O notation describes the worst-case performance of an algorithm by setting an upper bound on how its time or space requirements grow as input size increases. For example, O(n²) represents quadratic growth.
What is Big Theta notation?
Big Theta (Θ) notation represents a tight bound on an algorithm’s performance, meaning its growth rate is bounded both above and below by the same function. It shows when an algorithm’s best- and worst-case growth rates scale at the same rate.
When should I use Big O vs. Big Theta?
Big O notation is used to analyze worst-case behavior, which is important for understanding system performance under heavy load.
Big Theta notation is used when an algorithm’s upper and lower bounds match, meaning its performance scales consistently across inputs.





