Bubble Sort Time Complexity and Algorithm Explained

Bubble sort is a sorting algorithm that starts from the first element of an array and compares it with the second element. If the first element is greater than the second, we swap them. It continues this process until the end of the array, with the largest elements “bubbling” to the top. Its worst-case time complexity is O(n²), and its best-case time complexity is O(n).

As software engineers and data scientists, sorting functions like bubble sort play a vital role in the technologies we use every day. While most programming languages come with built-in functions for common sorting algorithms, knowing how sorting algorithms function allows us to make more informed decisions about which one to use based on its space and time complexities, especially when working with large data sets.

In this article, we’ll dive into the bubble sort algorithm, how it works and examine its implementation in Python and JavaScript.

What Is Bubble Sort?

The bubble sort algorithm arranges an array or string of elements into ascending or descending order. It sorts elements by comparing adjacent elements from left to right in an array, and swapping the elements if they are out of order.

To sort an array [2, 3, 4, 5, 1] in ascending order using the bubble sort algorithm, we start from the first element [2] and compare it with the second element [3]. If the first element is greater than the second, we swap them. We continue this process of comparing pairs of elements until we reach the end of the array. This way, the largest elements will be shifted to the end of the array, and the smallest elements will be shifted to the beginning of the array.

The name “bubble sort” refers to the way in which larger elements “bubble” to the top or the end of the array, as they are repeatedly compared and swapped with smaller elements when sorted in ascending order. By the end of an ascending sorting process, the array will be fully sorted from smallest to largest elements.

RelatedHeap Sort Explained

How the Bubble Sort Algorithm Works

Let’s look at the bubble sort algorithm in action. The following is a list of unordered numbers that we will use bubble sort to organize:

The first step is to focus only on the first two numbers, which in this example are 5 and 9. You can visualize considering just the two elements 5 and 9 as shown in the image below:

Then, you must determine if the numbers inside the bubble are in order. If they aren’t in proper order, switch them around to make it right. Fortunately for us, they are already arranged in ascending order. 5 is less than 9, so it comes before 9. This means we don’t have anything left to do. We move our bubble one step further like this:

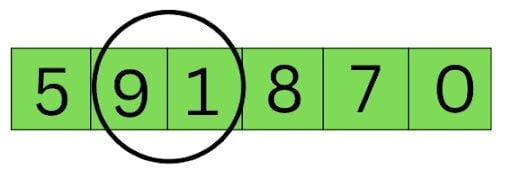
We conduct the same step in the next iteration of the array. However, this time 9 is greater than 1, but it’s also in front of it. So, to rectify that, the position of both elements is swapped. Here’s how the list looks now:

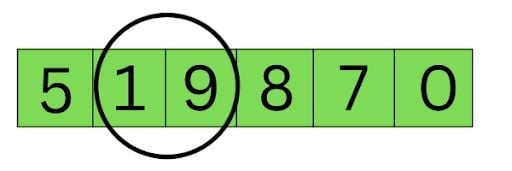
Now that the elements are swapped, the bubble progresses to successive pairs. And the steps repeat until the last pairs in the array have undergone a check to swap. The first run through the array will look like this:

The bubble sort algorithm is a simple yet effective way to sort an array of elements. It works by repeatedly iterating through the array and comparing pairs of elements, swapping their positions if they are out of order. This process is repeated until the entire array is sorted.

One thing to remember is that the number of passes required to sort an array is equal to the number of elements in the array. For example, a six-element array will need to go through six passes in order to be fully sorted in ascending order.

However, it’s possible to make the bubble sort algorithm more efficient by limiting the number of operations or passes conducted on the array. This is because the last element of the array is always the maximum value, so there is no need to continue comparing all elements beyond this point in future passes through the array. We’ll see this optimization in action as we implement the bubble sort algorithm in Python and JavaScript in later sections.

RelatedQuicksort Algorithm: An Overview

Bubble Sort Time and Space Complexity

Data scientists must understand the performance of a sorting algorithm and how much time/space it requires. This allows you to select the best sorting algorithm depending on your specific situation, as many options are available.

When bubble sort is used on an array already in ascending order, it requires only one pass through the entire array. This is considered the best-case scenario. In practice, though, this only occurs sometimes, and bubble sort usually necessitates n(n-1)/2 swaps or comparisons to achieve a sorted array.

The bubble sort algorithm’s average/worst time complexity is O(n²), as we have to pass through the array as many times as there are pairs in a provided array. Therefore, when time is a factor, there may be better options.

• Worst-case time complexity: O(n²).
• Average time complexity: O(n²).
• Best-case time complexity: O(n), the array is already sorted.

In terms of space complexity, since we only swapped the elements with one another and never stored anything, we don’t need any extra space to run the algorithm. This is amazing because it means the space complexity comes out as constant, or O(1). This makes it an in-place algorithm that works by modifying the input directly.

How to Implement Bubble Sort in Python

This section implements the bubble sort algorithm using Python. We’ll observe a naive implementation and a more efficient version of the bubble sort algorithm.

Initialize a Python array containing integer elements:

unsortedData = [20, 33, 12, 53, 24, 65, 23, 4, 53, 1];

Define a function named bubbleSort that accepts an array in its parameter named data. First, let’s attempt to pass through the array that swaps any elements that satisfy the condition that if the left element at a particular index is greater than an element to the right, we execute a swap operation between those two elements.

One thing to note is the assignment of the left element in any iteration to a temporary variable tempValue and then assigning the right element to the temporary variable.

def bubbleSort(data):
    
    for i in range(0, len(data)):
        if i+1 < len(data):
            if data[i] > data[i+1]:
                tempValue = data[i]
                data[i] = data[i+1]
                data[i+1] = tempValue
    
    return data

The code snippet above, when called with an unsorted array passed as its arguments, will conduct the bubbleSort function pass once on the array. And in most cases, it won’t completely sort the array in ascending order.

sortedData = bubbleSort(unsortedData)
print(sortedData)
>>>[20, 12, 33, 24, 53, 23, 4, 53, 1, 65]

To fix this, we have to iterate through the array we want to sort as many times as there are combinations of pairs. The number of iterations to conduct is the length of the unsorted array squared (len(unsortedArrray)²). This is the naive implementation.

def bubbleSort(data):

    # Iterate through the array enough times to consider every possible swap pairs
    for _ in range(0, len(data)): 
        for i in range(0, len(data)):
            if i+1 < len(data):
                if data[i] > data[i+1]:
                    tempValue = data[i]
                    data[i] = data[i+1]
                    data[i+1] = tempValue
    
    return data

Running the bubble sort function again with the unsorted array passed as an argument will result in an array sorted in ascending order provided as an output.

sortedData = bubbleSort(unsortedData)
print(sortedData)
>>> [1, 4, 12, 20, 23, 24, 33, 53, 53, 65]

Bubble Sort Algorithm Optimized

While the naive version of the bubble sort algorithm does work, it has some unnecessary and redundant operations. In particular, it compares elements at the end of the array that are already the maximum values present in the array. This is because on each pass through the array, the bubble sort algorithm moves the maximum element values to the end of the array.

To optimize the bubble sort algorithm, we can reduce the number of swap operations required by keeping track of the portion of the array that we want to consider for comparison. We can do this by starting with the maximum length of the array and decrementing it by one after each pass, reducing the area of the array that the swap operation acts upon. This way, we can avoid comparing with the last elements of the array on each pass, which are already in their correct position.

By using this optimization, we can make the bubble sort algorithm more efficient and reduce the number of unnecessary operations it performs.

unsortedData = [20, 33, 12, 53, 24, 65, 23, 4, 53, 1];
end = len(unsortedData)

def bubbleSort(data):
    global end
    for _ in range(0, end):
        for i in range(0, end):
            if i+1 < end:
                if data[i] > data[i+1]:
                    tempValue = data[i]
                    data[i] = data[i+1]
                    data[i+1] = tempValue
    end = end - 1
    return data

sortedData = bubbleSort(unsortedData)
print(sortedData)
>>> [1, 4, 12, 20, 23, 24, 33, 53, 53, 65]

Further refactoring could be conducted to ensure the code above is readable and efficient.

unsortedData = [20, 33, 12, 53, 24, 65, 23, 4, 53, 1]
n = len(unsortedData)

def bubbleSort(data):
    for i in range(n):
        swapped = False
        for j in range(0, n-i-1):
            if data[j] > data[j+1]:
                data[j], data[j+1] = data[j+1], data[j]
                swapped = True
        if not swapped:
            break
    return data

sortedData = bubbleSort(unsortedData)
print(sortedData)

Below is an implementation of the same algorithm in JavaScript, a programming language popular with data practitioners and software engineers.

How to Implement the Bubble Sort Algorithm in JavaScript

const unsortedData = [20, 33, 12, 53, 24, 65, 23, 4, 53, 1];
let end = unsortedData.length - 1

const bubbleSort = (data) => {
    
    for (let i = 0; i < end; i++) {
        if (data[i] > data[i + 1]) {
            const valueInRight = data[i]
            data[i] = data[i+1]
            data[i+1] = valueInRight
        }
    }
    end--
}

for (let i = 0; i < unsortedData.length; i++) {
    bubbleSort(unsortedData)
}

console.log(unsortedData)

More on Data ScienceFull vs. Complete Binary Tree: What’s the Difference?

Bubble Sort Algorithm Advantages

The bubble sort algorithm may not be the most well-known or highly-regarded sorting algorithm, but it’s not a terrible option either. With a time complexity of O(n²) and a space complexity of O(1), it’s a simple algorithm that is easy for beginners to understand. However, its slow speed may make it less practical for certain applications.

Despite its limitations, the bubble sort algorithm can be a useful starting point for learning about sorting algorithms and data structures. It’s a good way to get a basic understanding of how these algorithms work, and can help you build a foundation for learning more complex algorithms later on.

That being said, the bubble sort algorithm may not be the best choice for time-sensitive material, as its slow speed can be prohibitive. However, if you’re willing to sacrifice some space for time, it may work well for you. Ultimately, whether you will use the bubble sort algorithm will depend on your specific needs and goals.

Frequently Asked Questions