At their core, data scientists have a math and statistics background. Out of this math background, they’re creating advanced analytics. On the extreme end of this applied math, they’re creating machine learning models and artificial intelligence. Just like their software engineering counterparts, data scientists will have to interact with the business side. This includes understanding the domain enough to make insights. Data scientists are often tasked with analyzing data to help the business, and this requires a level of business acumen. Finally, their results need to be given to the business in an understandable fashion. This requires the ability to verbally and visually communicate complex results and observations in a way that the business can understand and act on them.
Thus, it’ll be extremely valuable for any aspiring data scientists to learn data mining — the process where one structures the raw data and formulate or recognize the various patterns in the data through the mathematical and computational algorithms. This helps to generate new information and unlock various insights.
Here is a simple list of reasons on why you should study data mining?
-
There is a heavy demand for deep analytical talent at the moment in the tech industry.
-
You can gain a valuable skill if you want to jump into Data Science / Big Data / Predictive Analytics.
-
Given lots of data, you’ll be able to discover patterns and models that are valid, useful, unexpected, and understandable.
-
You can find human-interpretable patterns that describe the data (Descriptive), or
-
Use some variables to predict unknown or future values of other variables (Predictive).
-
You can activate your knowledge in CS theory, Machine Learning and Databases.
-
Last but not least, you’ll learn a lot about algorithms, computing architectures, data scalability, and automation for handling massive datasets.
In my last semester in college, I did an independent study on Big Data. The class covers extensive materials in a book titled Mining of Massive Datasets by Leskovec, Rajaraman and Ullman. We discussed a lot of important algorithms and systems in Big Data such as MapReduce, Social Graph, Clustering…. This experience deepened my interest in the Data Mining academic field and convinced me to specialize further in it. I took again Stanford CS246’s Mining of Massive Datasets, which covered that book and featured lectures from the authors.
Now being exposed to that content twice, I want to share the 10 mining techniques from the book that I believe any data scientists should learn to be more effective while handling big datasets.
10 Data Mining Techniques to Know
- MapReduce
- Distance measures
- Data streaming
- Link analysis
- Frequent itemset analysis
- Clustering
- Computational advertising
- Recommendation systems
- Social network graphs
- Dimensionality reduction
1. MapReduce
Modern data-mining applications require us to manage immense amounts of data quickly. In many of these applications, the data is extremely regular, and there is ample opportunity to exploit parallelism. To deal with applications such as these, a new software stack has evolved. These programming systems are designed to get their parallelism not from a “super-computer,” but from “computing clusters” — large collections of commodity hardware, including conventional processors connected by Ethernet cables or inexpensive switches.
The software stack begins with a new form of a file system, called “distributed file system,” which features much larger units than the disk blocks in a conventional operating system. Distributed file systems also provide replication of data or redundancy to protect against the frequent media failures that occur when data is distributed over thousands of low-cost compute nodes.
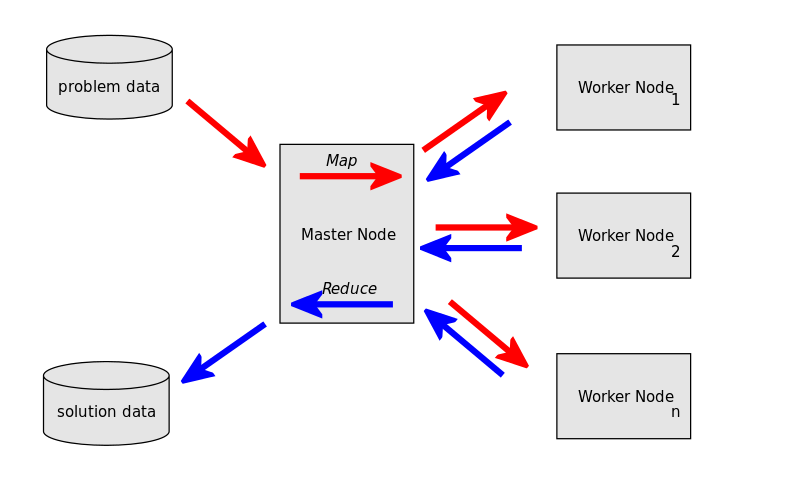
On top of these file systems, many different higher-level programming systems have been developed. Central to the new software stack is a programming system called MapReduce. It is a style of computing that has been implemented in several systems, including Google’s internal implementation and the popular open-source implementation Hadoop which can be obtained, along with the HDFS file system from the Apache Foundation. You can use an implementation of MapReduce to manage many large-scale computations in a way that is tolerant of hardware faults. All you need to write are 2 functions, called Map and Reduce, while the system manages the parallel execution, coordination of tasks that execute Map or Reduce, and also deals with the possibility that one of these tasks will fail to execute.
In brief, a MapReduce computation executes as follows:
-
Some number of Map tasks each are given one or more chunks from a distributed file system. These Map tasks turn the chunk into a sequence of key-value pairs. The way key-value pairs are produced from the input data is determined by the code written by the user for the Map function.
-
The key-value pairs from each Map task are collected by a master controller and sorted by key. The keys are divided among all the Reduce tasks, so all key-value pairs with the same key wind up at the same Reduce task.
-
The Reduce tasks work on one key at a time and combine all the values associated with that key in some way. The manner of combination of values is determined by the code written by the user for the Reduce function.
Here is a notebook with sample implementations of MapReduce.
2. Distance Measures

A fundamental data mining problem is to examine data for “similar” items. An example would be looking at a collection of Web pages and finding near-duplicate pages. These pages could be plagiarisms, for example, or they could be mirrors that have almost the same content but differ in information about the host and about other mirrors. Other examples might include finding customers who purchased similar products or finding images with similar features.
Distance Measure is simply a data mining technique to deal with this problem: finding near-neighbors (points that are a small distance apart) in a high-dimensional space. For each application, we first need to define what “similarity” means. The most common definition in data mining is the Jaccard Similarity. The Jaccard similarity of sets is the ratio of the size of the intersection of the sets to the size of the union. This measure of similarity is suitable for many applications, including textual similarity of documents and similarity of buying habits of customers.
Let’s take the task of finding similar documents as an example. There are many problems here: many small pieces of one document can appear out of order in another, too many documents to compare all pairs, documents are so large or so many that they cannot fit in main memory… In order to deal with these, there are 3 essential steps for finding similar documents:
-
Shingling: Convert documents to sets.
-
Min-Hashing: Convert large sets to short signatures, while preserving similarity.
-
Locality-Sensitive Hashing: Focus on pairs of signatures likely to be from similar documents.
The most effective way to represent documents as sets, for the purpose of identifying lexically similar documents, is to construct from the document the set of short strings that appear within it.
-
A k-shingle is any k characters that appear consecutively in a document. In shingling, if we represent a document by its set of k-shingles, then the Jaccard similarity of the shingle sets measures the textual similarity of documents. Sometimes, it is useful to hash shingles to bit strings of shorter length, and use sets of hash values to represent documents.
-
A min-hash function on sets is based on a permutation of the universal set. Given any such permutation, the min-hash value for a set is that element of the set that appears first in the permuted order. In min-hashing, we may represent sets by picking some list of permutations and computing for each set its min-hash signature, which is the sequence of min-hash values obtained by applying each permutation on the list to that set. Given 2 sets, the expected fraction of the permutations that will yield the same min-hash value is exactly the Jaccard similarity of the sets.
-
Locality-Sensitive Hashing allows us to avoid computing the similarity of every pair of sets or their min-hash signatures. If we are given signatures for the sets, we may divide them into bands, and only measure the similarity of a pair of sets if they are identical in at least one band. By choosing the size of bands appropriately, we can eliminate from consideration most of the pairs that do not meet our threshold of similarity.
Here is a notebook with sample implementations of Distance Measures.
3. Data Streaming
In many data mining situations, we do not know the entire dataset in advance. Sometimes, data arrives in a stream or streams, and if it is not processed immediately or stored, then it is lost forever. Moreover, the data arrives so rapidly that it is not feasible to store it all in an active storage and then interact with it at the time of our choosing. In other words, the data is infinite and non-stationary (the distribution changes over time — think Google queries or Facebook status updates). Stream Management thus becomes very important.
In a data stream management system, any number of streams can enter the system. Each stream can provide elements at its own schedule; they need not have the same data rates or data types, and the time between elements of one stream need not be uniform. Streams may be archived in a large archival store, but it is not possible to answer queries from the archival store. It could be examined only under special circumstances using time-consuming retrieval processes. There is also a working store, into which summaries or parts of streams may be placed, and which can be used for answering queries. The working store might be the disk, or it might be the main memory, depending on how fast we need to process queries. But either way, it is of sufficiently limited capacity that it cannot store all the data from all the streams.
Problems in Data Streaming
There are a variety of problems in data streaming, of which I go over 3 of them here:
-
Sampling Data in a Stream: The general problem is to select a subset of a stream so that we can ask queries about the deleted subset and have the answers to be statistically representative of the stream as a whole. To create a sample of a stream that is usable for a class of queries, we identify a set of key attributes for the stream. By hashing the key of any arriving stream element, we can use the hash value to decide consistently whether all or none of the elements with that key will become part of the sample.
-
Filtering Streams: We want to accept the tuples in the stream that meet a criterion. Accepted tuples are passed to another process as a stream, while other tuples are dropped. Bloom Filtering is a great technique that can filter streams so elements that belong to a particular set are allowed through, while most non-members are deleted. We use a large bit array and several hash functions. Members of the selected set are hashed to buckets, which are bits in the array, and those bits are set to 1. To test a stream element for membership, we hash the element to a set of bits using each of the hash functions and only accept the element if all bits are 1.
-
Counting Distinct Elements in a Stream: Suppose stream elements are chosen from some universal set. We would like to know how many different elements have appeared in the stream, counting either from the beginning of the stream or from some known time in the past. Flajolet-Martin is a technique that hashes elements to integers, interpreted as binary numbers. By using many hash functions and combining these estimates, first by taking averages within groups, and then taking the median of the averages, we get a reliable estimate.
Here is a notebook with sample implementations of Stream Algorithms.
4. Link Analysis
One of the biggest changes in our lives in the decade following the turn of the century was the availability of efficient and accurate Web search, through search engines such as Google. Early search engines were unable to deliver relevant results because they were vulnerable to term spam — the introduction into Web pages of words that misrepresented what the page was about. While Google was not the first search engine, it was the first able to counteract term spam by 2 techniques:
-
PageRank was used to simulate where Web surfers, starting at a random page, would tend to congregate if they followed randomly chosen outlines from the page at which they were currently located, and this process was allowed to iterate many times. Pages that would have a large number of surfers were considered more “important” than pages that would rarely be visited. Google prefers important pages to unimportant pages when deciding which pages to show first in response to a search query.
-
The content of a page was judged not only by the terms appearing on that page but by the terms used in or near the links to that page. Note that while it is easy for a spammer to add false terms to a page they control, they cannot as easily get false terms added to the pages that link to their own page, if they do not control those pages.
PageRank

Let’s dig a bit deeper into PageRank: It is a function that assigns a real number to each page in the Web. The intent is that the higher of the PageRank of a page, the more “important” it is. There is not one fixed algorithm for assignment of PageRank, and in fact variations on the basic idea can alter the relative PageRank of any 2 pages. In its simplest form, PageRank is a solution to the recursive equation “a page is important if important pages link to it.”
How to Calculate PageRank
For strongly connected Web graphs (those where any node can reach any other node), PageRank is the principal eigenvector of the transition matrix. We can compute PageRank by starting with any non-zero vector and repeatedly multiplying the current vector by the transition matrix, to get a better estimate. After about 50 iterations, the estimate will be very close to the limit, which is the true PageRank.
Calculation of PageRank can be thought of as simulating the behavior of many random surfers, who each start at a random page and at any step move, at random, to one of the pages to which their current page links. The limiting probability of a surfer being at a given page is the PageRank of that page. The intuition is that people tend to create links to the pages they think are useful, so random surfers will tend to be at a useful page.
How to Improve PageRank
There are several improvements we can make to PageRank. One, called Topic-Sensitive PageRank, is that we can weigh certain pages more heavily because of their topic. If we know the query-er is interested in a certain topic, then it makes sense to bias the PageRank in favor of pages on that topic. To compute this form of PageRank, we identify a set of pages known to be on that topic, and we use it as a “teleport set.” The PageRank calculation is modified so that only the pages in the teleport set are given a share of the tax, rather than distributing the tax among all pages on the Web.
When it became apparent that PageRank and other techniques used by Google made term spam ineffective, spammers turned to methods designed to fool the PageRank algorithm into overvaluing certain pages. The techniques for artificially increasing the PageRank of a page are collectively called Link Spam. Typically, a spam farm consists of a target page and very many supporting pages. The target page links to all the supporting pages and the supporting pages link only to the target page. In addition, it is essential that some links from outside the spam farm be created. For example, the spammer might introduce links to their target page by writing comments in other people’s blogs or discussion groups.
One way to ameliorate the effect of link spam is to compute a topic-sensitive PageRank called TrustRank, where the teleport set is a collection of trusted pages. For example, the home pages of universities could serve as the trusted set. This technique avoids sharing the tax in the PageRank calculation with the large numbers of supporting pages in spam farms and thus preferentially reduces their PageRank. To identify spam farms, we can compute both the conventional PageRank and the TrustRank for all pages. Those pages that have much lower TrustRank than PageRank are likely to be part of a spam farm.
Here is a notebook with sample implementations of Link Analysis.
5. Frequent Itemset Analysis
The market-basket model of data is used to describe a common form of many-many relationship between 2 kinds of objects. On the one hand, we have items, and on the other, we have baskets. Each basket consists of a set of items (an item-set), and usually we assume that the number of items in a basket is small — much smaller than the total number of items. The number of baskets is usually assumed to be very large, bigger than what can fit in main memory. The data is assumed to be represented in a file consisting of a sequence of baskets. In terms of the distributed file system, the baskets are the objects of the file, and each basket is of type “set of items.”
Thus, one of the major families of data mining techniques for characterizing data based on this market-basket model is the discovery of frequent itemsets, which are basically sets of items that appear in many baskets. The original application of the market-basket model was in the analysis of true market baskets. That is, supermarkets and chain stores record the contents of every market basket brought to the register for checkout. Here the items are the different products that the store sells, and the baskets are the sets of items in a single market basket. However, the same model can be used to mine many other kinds of data, such as:
-
Related concepts: Let items be words, and let baskets be documents (webpages, blogs, tweets). A basket / document contains those items / words that are present in the document. If we look for sets of words that appear together in many documents, the sets will be dominated by the most common words (stop words). There, even though the intent was to find snippets that talked about cats and dogs, the stop words “and” and “a” were prominent among the frequent item sets. However, if we ignore all the most common words, then we would hope to find among the frequent pairs some pairs of words that represent a joint concept.
-
Plagiarism: Let the items be documents and the baskets be sentences. An item / document is “in” a basket / sentence if the sentence is in the document. This arrangement appears backwards, but it is exactly what we need, and we should remember that the relationship between items and baskets is an arbitrary many-many relationship. That is, “in” need not have its conventional meaning: “part of.” In this application, we look for pairs of items that appear together in several baskets. If we find such a pair, then we have 2 documents that share several sentences in common. In practice, even 1 or 2 sentences in common is a good indicator of plagiarism.
-
Biomarkers: Let the items be of 2 types — biomarkers such as genes or blood proteins, and diseases. Each basket is the set of data about a patient: their genome and blood-chemistry analysis, as well as their medical history of the disease. A frequent item-set that consists of one disease and one or more biomarkers suggests a test for the disease.

Frequent Itemset Properties
Here are the main properties of frequent itemsets that you definitely should know:
-
Association Rules: These are implications that if a basket contains a certain set of items i, then it is likely to contain another particular item j as well.
-
Pair-Counting Bottleneck: For typical data, with a goal of producing a small number of item-sets that are the most frequent of all, the part that often takes the most main memory is the counting of pairs of items. Thus, methods for finding frequent item-sets typically concentrate on how to minimize the main memory needed to count pairs.
-
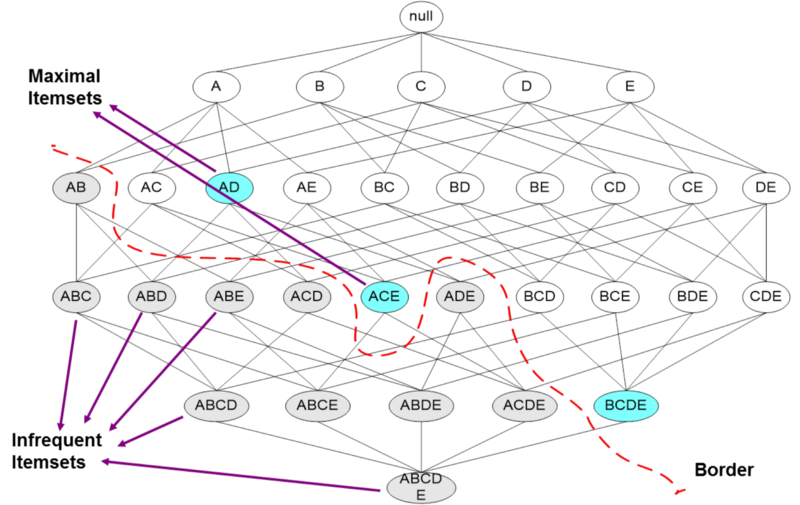
Monotonicity: An important property of item-sets is that if a set of items is frequent, then so are all its subsets.
Algorithms for Finding Frequent Itemsets
There are a variety of algorithms for finding frequent itemsets. I go over some important ones below:
-
A-Priori: We can find all frequent pairs by making two passes over the baskets. On the first pass, we count the items themselves and then determine which items are frequent. On the second pass, we count only the pairs of items both of which are found frequently on the first pass. Monotonicity justifies our ignoring other pairs.
-
PCY (Park, Chen, Yu): This algorithm improves on A-Priori by creating a hash table on the first pass, using all main-memory space that is not needed to count the items. Pairs of items are hashed, and the hash-table buckets are used as integer counts of the number of times a pair has hashed to that bucket. Then, on the second pass, we only have to count pairs of frequent items that hashed to a frequent bucket (one whose count is at least the support threshold) on the first pass.

-
Multi-stage: We can insert additional passes between the first and second pass of the PCY Algorithm to hash pairs to other, independent hash tables. At each intermediate pass, we only have to hash pairs of frequent items that have hashed to frequent buckets on all previous passes.
-
Multi-hash: We can modify the first pass of the PCY Algorithm to divide available main memory into several hash tables. On the second pass, we only have to count a pair of frequent items if they hashed to frequent buckets in all hash tables.
-
Randomized: Instead of making passes through all the data, we may choose a random sample of the baskets, small enough that it is possible to store both the sample and the needed counts of item-sets in main memory. The support threshold must be scaled down in proportion. We can then find the frequent item-sets for the sample and hope that it is a good representation of the data as a whole. While this method uses at most one pass through the whole dataset, it is subject to false positives (item-sets that are frequent in the sample but not the whole) and false negatives (item-sets that are frequent in the whole but not the sample).
Here is a notebook with sample implementations of Frequent Itemsets Analysis.
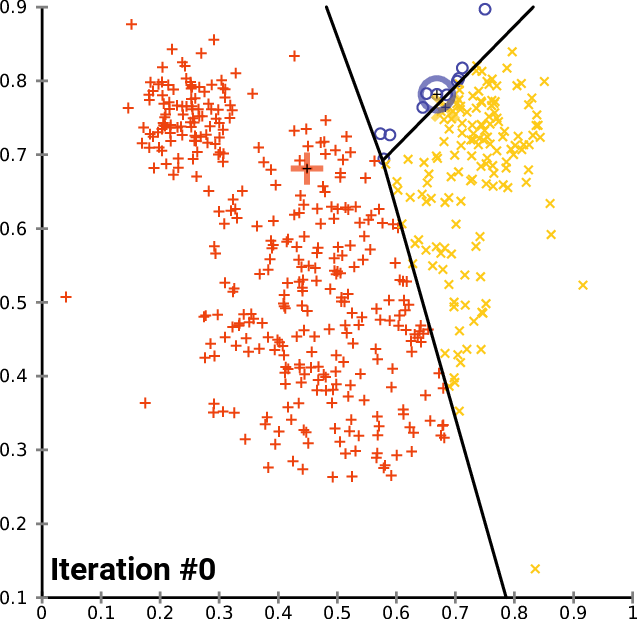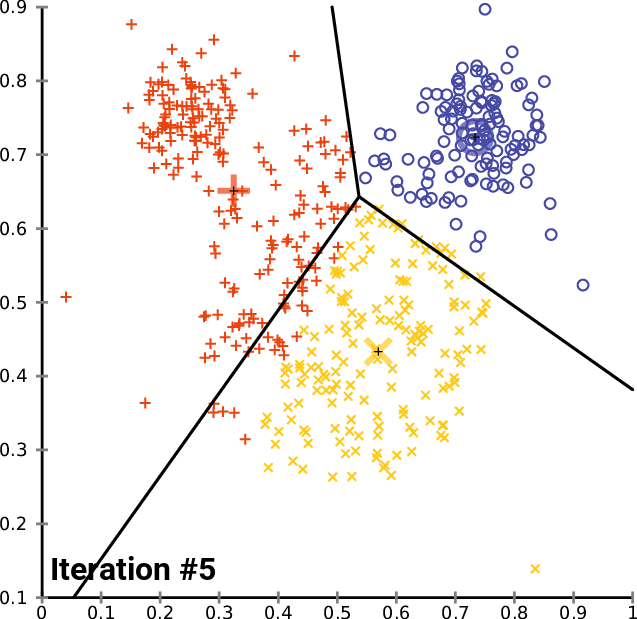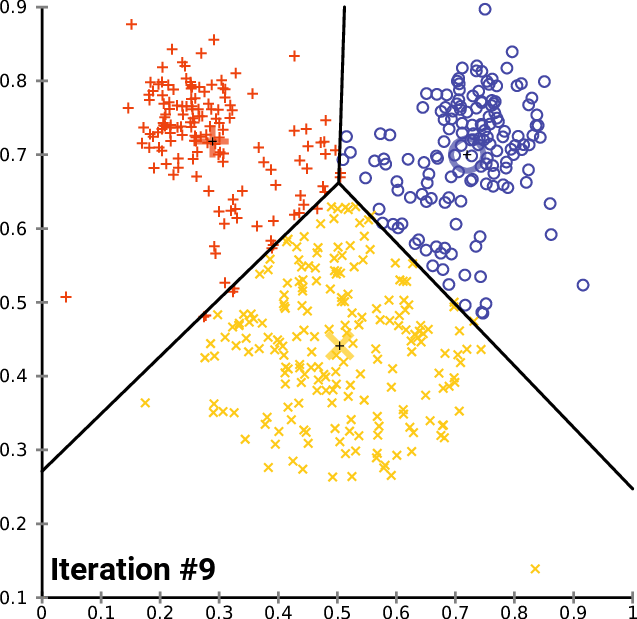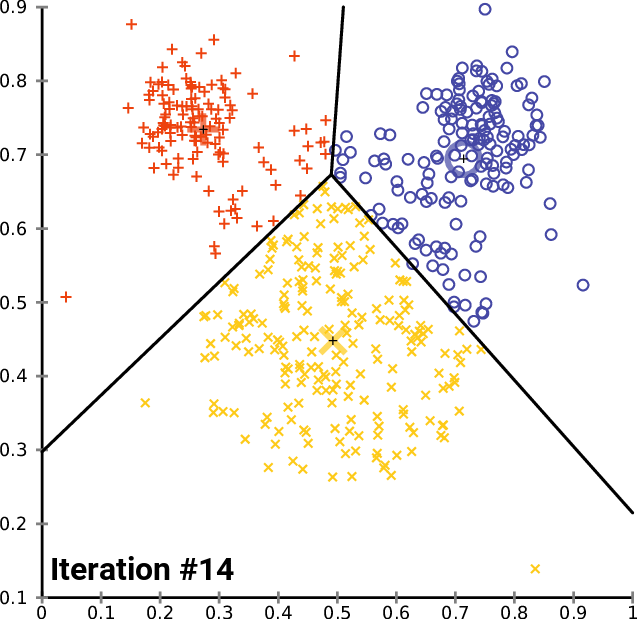
6. Clustering
An important component in big data analysis is high-dimensional data — essentially datasets with a large number of attributes or features. In order to deal with high-dimensional data, clustering is the process of examining a collection “points,” and grouping the points into “clusters” according to some distance measure. The goal is that points in the same cluster have a small distance from one another, while points in different clusters are at a large distance from one another. The typical distance measures being used are Euclidean, Cosine, Jaccard, Hamming and Edit.
Types of Clustering Algorithms
We can divide clustering algorithms into 2 groups that follow 2 fundamentally different strategies:
-
Hierarchical / Agglomerative algorithms start with each point in its own cluster. Clusters are combined based on their closeness, using one of many possible definitions of close. Combination stops when further combination leads to clusters that are undesirable for one of several reasons. For example, we may stop when we have a predetermined number of clusters, or we may use a measure of compactness for clusters, and refuse to construct a cluster by combining 2 smaller clusters if the resulting cluster has points that are spread out over too large a region.
-
The other class of algorithms involves point assignment. Points are considered in some order, and each one is assigned to the cluster into which it best fits. This process is normally preceded by a short phase in which initial clusters are estimated. Variations allow occasional combining or splitting of clusters, or may allow points to be unassigned if they are outliers (points too far from any of the current clusters).
Hierarchical Clustering
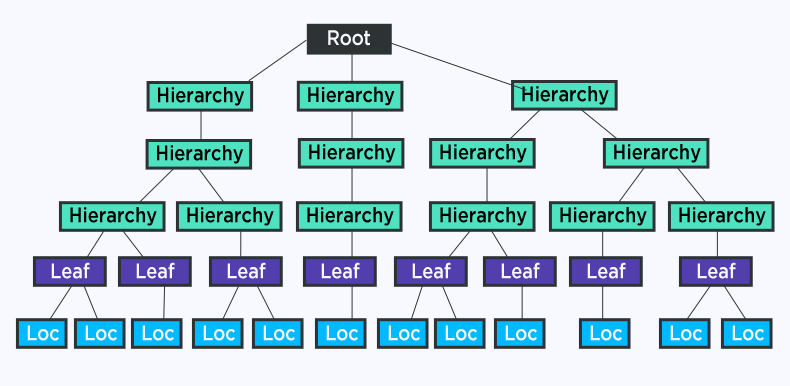
In hierarchical clustering, we repeatedly combine the 2 nearest clusters. This family of algorithms has many variations, which differ primarily in 2 areas: choosing how 2 clusters can merge and deciding when to stop the merging process.
-
For picking clusters to merge, one strategy is to pick the clusters with the closest centroids (average member of clusters in Euclidean space) or clustroids (representative member of the cluster in non-Euclidean space). Another approach is to pick the pair of clusters with the closest points, one from each cluster. A 3rd approach is to use the average distance between points from the 2 clusters.
-
For stopping the merger process, a hierarchical clustering can proceed until there are a fixed number of clusters left. Alternatively, we could merge until it is impossible to find a pair of clusters whose merger is sufficiently compact. Another approach involves merging as long as the resulting cluster has a sufficiently high density, which is the number of points divided by some measure of the size of the cluster.
Point Assignment Clustering
On the other hand, there are a variety of point assignment clustering algorithms:
-
K-Means: Assuming a Euclidean space, there are exactly k clusters for some known k. After picking k initial cluster centroids, the points are considered one at a time and assigned to the closest centroid. The centroid of a cluster can migrate during point assignment, and an optional last step is to reassign all the points while holding the centroids fixed at their final values obtained during the first pass.
-
BFR (Bradley, Fayyad, Reina): This algorithm is a version of k-means designed to handle data that is too large to fit in main memory. It assumes clusters are normally distributed about the axes.
-
CURE (Clustering Using Representatives): This algorithm is designed for a Euclidean space, but clusters can have any shape. It handles data that is too large to fit in main memory.
7. Computational Advertising
One of the big surprises of the 21st century has been the ability of all sorts of interesting Web applications to support themselves through advertising, rather than subscription. The big advantage that Web-based advertising has over advertising in conventional media is that Web advertising can be selected according to the interests of each individual user. This advantage has enabled many Web services to be supported entirely by advertising revenue. By far the most lucrative venue for online advertising has been search, and much of the effectiveness of search advertising comes from the “Adwords” model of matching search queries to advertisements. Before addressing the question of matching advertisements to search queries, we shall digress slightly by examining the general class to which such algorithms belong.
Conventional algorithms that are allowed to see all their data before producing an answer are called offline. An online algorithm is required to make a response to each element in a stream immediately, with knowledge of only the past, not the future elements in the stream. Many online algorithms are greedy, in the sense that they select their action at every step by minimizing some objective function. We can measure the quality of an online algorithm by minimizing the competitive ratio — the value of the result of the online algorithm compared with the value of the result of the best possible offline algorithm.

Let’s consider the fundamental problem of search advertising — the Adwords problem — because it was first encountered in the Google Adwords system. Google Adwords is a form of search ad management, in which a search engine (Google) receives bids from advertisers on certain search queries. Some ads are displayed with each search query, and the search engine is paid the amount of the bid only if the query-er clicks on the ad. Each advertiser can give a budget, the total amount they are willing to pay for clicks in a month.
The data for the Adwords problem is a set of bids by advertisers on certain search queries, together with a total budget for each advertiser and information about the historical click-through rate for each ad for each query. Another part of the data is the stream of search queries received by the search engine. The objective is to select online a fixed set of ads in response to each query that will maximize the revenue to the search engine.
How to Solve the AdWords Problem
Generally, there are 2 approaches to solve the Adwords problem (we considered a simplified version in which all bids are either 0 or 1, only one ad is shown with each query, and all advertisers have the same budget):
-
The Greedy Approach: Under the simplified Adwords model, the obvious greedy algorithm of giving the ad placement to anyone who has bid on the query and has budget remaining can be shown to have a competitive ratio of 1/2.
-
The Balance Algorithm: This algorithm improves on the simple greedy algorithm. A query’s ad is given to the advertiser who has bid on the query and has the largest remaining budget. Ties can be broken arbitrarily. For the simplified Adwords model, the competitive ratio of the Balance Algorithm is 3/4 for the case of two advertisers and 1−1/e, or about 63% for any number of advertisers.

While we should now have an idea of how ads are selected to go with the answer to a search query, we have not addressed the problem of finding the bids that have been made on a given query. In other words, how can we implement Adwords?
-
The simplest version of the implementation serves in situations where the bids are on exactly the set of words in the search query. We can represent a query by the list of its words, in sorted order. Bids are stored in a hash table or similar structure, with a hash key equal to the sorted list of words. A search query can then be matched against bids by a straightforward lookup in the table.
-
A harder version of the Adwords implementation problem allows bids, which are still small sets of words as in a search query, to be matched against larger documents, such as emails or tweets. A bid set matches the document if all the words appear in the document, in any order and not necessarily adjacent.
Here is a notebook with sample implementations of Computational Advertising.
8. Recommendation Systems
There is an extensive class of Web applications that involve predicting user responses to options. Such a facility is called a recommendation system. I suppose that you have already been using a lot of them, from Amazon (items recommendation) to Spotify (music recommendation), from Netflix (movie recommendation) to Google Maps (route recommendation). The most common model for recommendation systems is based on a utility matrix of preferences. Recommendation systems deal with users and items. A utility matrix offers known information about the degree to which a user likes an item. Normally, most entries are unknown, and the essential problem of recommending items to users is predicting the values of the unknown entries based on the values of the known entries.
Types of Recommendation Systems
Recommendation systems use a number of different technologies. We can classify them into 2 broad groups:
-
Content-based systems examine properties of the items recommended. For instance, if a Netflix user has watched many science fiction movies, then recommend a movie classified in the database as having the “sci-fi” genre.
-
Collaborative filtering systems recommend items based on similarity measures between users and/or items. The items recommended to a user are those preferred by similar users. This sort of recommendation system can use the groundwork laid by distance measures and clustering (discussed above). However, these technologies by themselves are not sufficient, and there are some new algorithms that have proven effective for recommendation systems.
Content-Based Systems
In a content-based system, we must construct for item profile, which is a record or collection of records representing important characteristics of that item. Different kinds of items have different features on which content-based similarity can be based. Features of documents are typically important or unusual words. Products have attributes such as screen size for a television. Media such as movies have a genre and details such as actor or performer. Tags can also be used as features if they can be acquired from interested users.
Additionally, we can construct user profiles by measuring the frequency with which features appear in the items the user likes. We can then estimate the degree to which a user will like an item by the closeness of the item’s profile to the user’s profile. An alternative to constructing a user profile is to build a classifier for each user, e.g., a decision tree. The row of the utility matrix for that user becomes the training data, and the classifier must predict the response of the user to all items, whether or not the row had an entry for that item.
Collaborative Filtering Systems

In a collaborative filtering system, instead of using features of items to determine their similarity, we focus on the similarity of the user ratings for 2 items. That is, in place of the item-profile vector for an item, we use its column in the utility matrix. Further, instead of contriving a profile vector for users, we represent them by their rows in the utility matrix. Users are similar if their vectors are close according to some distance measure such as Jaccard or Cosine distance. Recommendation for a user U is then made by looking at the users that are most similar to U in this sense, and recommending items that these users like.
Since the utility matrix tends to be mostly blanks, distance measures often have too little data with which to compare 2 rows or 2 columns. A preliminary step, in which similarity is used to cluster users and/or items into small groups with strong similarity, can help provide more common components with which to compare rows or columns.
Here is a comprehensive notebook of which I built multiple movie recommendation systems.
9. Social Network Graphs
When we think of a social network, we think of Facebook, Twitter, Google+. The essential characteristics of a social network are:
-
There is a collection of entities that participate in the network. Typically, these entities are people, but they could be something else entirely.
-
There is at least one relationship between entities of the network. On Facebook or its ilk, this relationship is called friends. Sometimes the relationship is all-or-nothing; 2 people are either friends or they are not. However, in other examples of social networks, the relationship has a degree. This degree could be discrete; e.g. friends, family, acquaintances, or none as in Google+. It could be a real number; an example would be the fraction of the average day that 2 people spend talking to each other.
-
There is an assumption of non-randomness or locality. This condition is the hardest to formalize, but the intuition is that relationships tend to cluster. That is, if entity A is related to both B and C, then there is a higher probability than average that B and C are related.
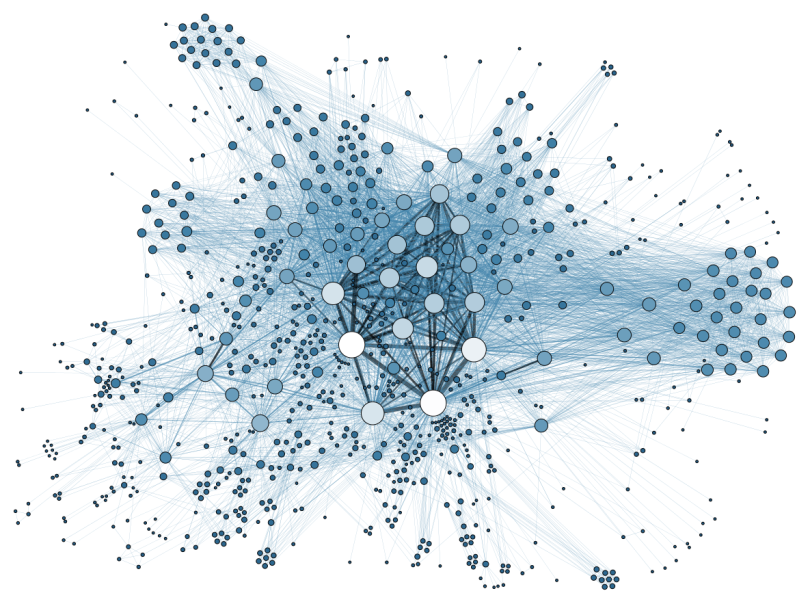
Social networks are naturally modeled as graphs, which we sometimes refer to as a social graph. The entities are the nodes, and an edge connects two nodes if the nodes are related by the relationship that characterizes the network. If there is a degree associated with the relationship, this degree is represented by labeling the edges. Often, social graphs are undirected, as for the Facebook friends graph. But they can be directed graphs, as for example the graphs of followers on Twitter or Google+.
Communities
An important aspect of social networks is that they contain communities of entities that are connected by many edges. These typically correspond to groups of friends at school or groups of researchers interested in the same topic, for example. To identify these communities, we need to consider ways to cluster the graph. While communities resemble clusters in some ways, there are also significant differences. Individuals (nodes) normally belong to several communities, and the usual distance measures fail to represent closeness among nodes of a community. As a result, standard algorithms for finding clusters in data do not work well for community finding.
One way to separate nodes into communities is to measure the betweenness of edges, which is the sum over all pairs of nodes of the fraction of shortest paths between those nodes that go through the given edge. Communities are formed by deleting the edges whose betweenness is above a given threshold. The Girvan-Newman Algorithm is an efficient technique for computing the betweenness of edges. A breadth-first search from each node is performed, and a sequence of labeling steps computes the share of paths from the root to each other node that goes through each of the edges. The shares for an edge that are computed for each root are summed to get the betweenness.
One way to find communities is to partition a graph repeatedly into pieces of roughly similar sizes. A cut is a partition of the nodes of the graph into two sets, and its size is the number of edges that have one end in each set. The volume of a set of nodes is the number of edges with at least one end in that set. We can normalize the size of a cut by taking the ratio of the size of the cut and the volume of each of the two sets formed by the cut. Then add these two ratios to get the normalized cut value. Normalized cuts with a low sum are good, in the sense that they tend to divide the nodes into two roughly equal parts and have a relatively small size.
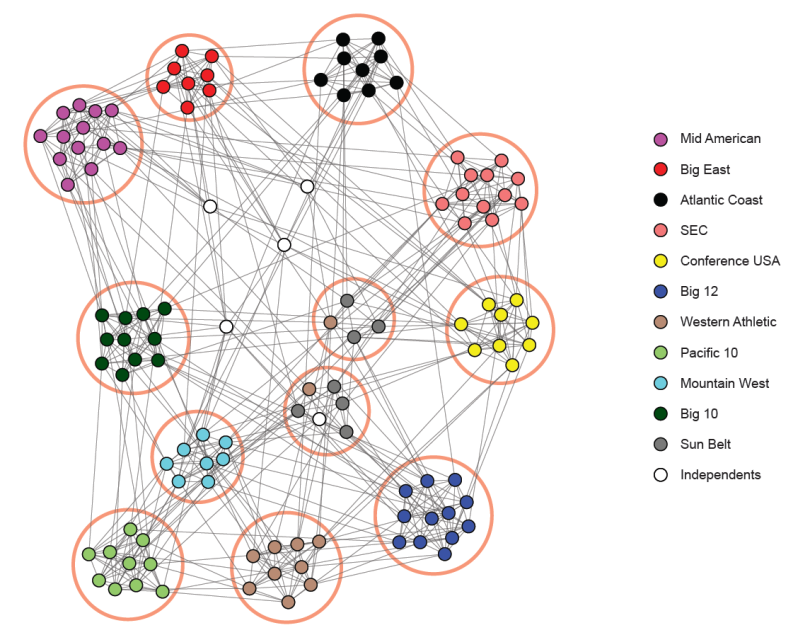
Typically, individuals are members of several communities. In graphs describing social networks, it is normal for the probability that two individuals are friends to rise as the number of communities of which both are members grows (hence the concept of overlapping communities). An appropriate model for membership in communities, known as the Affiliation-Graph Model, is to assume that for each community there is a probability that because of this community two members become friends (have an edge in the social network graph). Thus, the probability that two nodes have an edge is 1 minus the product of the probabilities that none of the communities of which both are members cause there to be an edge between them. We then find the assignment of nodes to communities and the values of those probabilities that best describes the observed social graph.
An important modeling technique, useful for modeling communities as well as many other things, is to compute, as a function of all choices of parameter values that the model allows, the probability that the observed data would be generated. The values that yield the highest probability are assumed to be correct and called the maximum-likelihood estimate (MLE).
10. Dimensionality Reduction
There are many sources of data that can be viewed as a large matrix. In Link Analysis, the Web can be represented as a transition matrix. In Recommendation Systems, the utility matrix was a point of focus. And in Social-Network Graphs, matrices represent social networks. In many of these matrix applications, the matrix can be summarized by finding “narrower” matrices that in some sense are close to the original. These narrow matrices have only a small number of rows or a small number of columns, and therefore can be used much more efficiently than can the original large matrix. The process of finding these narrow matrices is called dimensionality reduction.
The most fundamental concepts to know in dimensionality reduction are eigenvalues and eigenvectors. A matrix may have several eigenvectors such that when the matrix multiplies the eigenvector, the result is a constant multiple of the eigenvector. That constant is the eigenvalue associated with this eigenvector. Together the eigenvector and its eigenvalue are called an eigen-pair.
Principal Component Analysis (PCA)
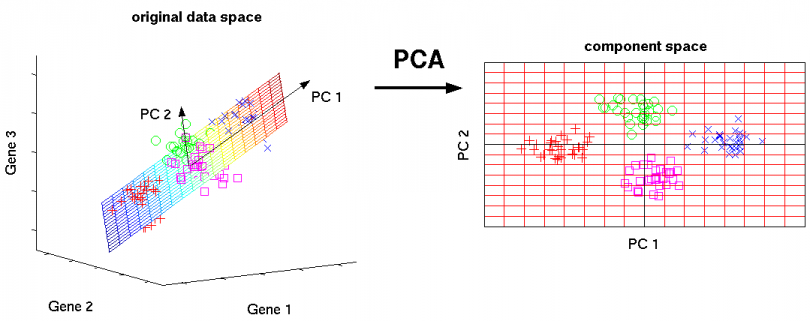
A powerful data mining technique for dimensionality reduction is Principal Component Analysis (PCA), which views data consisting of a collection of points in a multidimensional space as a matrix, with rows corresponding to the points and columns to the dimensions. The product of this matrix and its transpose has eigenpairs, and the principal eigenvector can be viewed as the direction in the space along which the points best line up. The second eigenvector represents the direction in which deviations from the principal eigenvector are the greatest, and so on. By representing the matrix of points by a small number of its eigenvectors, we can approximate the data in a way that minimizes the root-mean-square error for the given number of columns in the representing matrix.
Singular Value Decomposition (SVD)
Another form of matrix analysis that leads to a low-dimensional representation of a high-dimensional matrix is Singular Value Decomposition (SVD), which allows an exact representation of any matrix, and also makes it easy to eliminate the less important parts of that representation to produce an approximate representation with any desired number of dimensions. Of course, the fewer the dimensions we choose, the less accurate will be the approximation. The singular-value decomposition of a matrix consists of three matrices, U, Σ, and V. The matrices U and V are column-orthonormal, meaning that as vectors, the columns are orthogonal, and their lengths are 1. The matrix Σ is a diagonal matrix, and the values along its diagonal are called singular values. The product of U, Σ, and the transpose of V equals the original matrix.
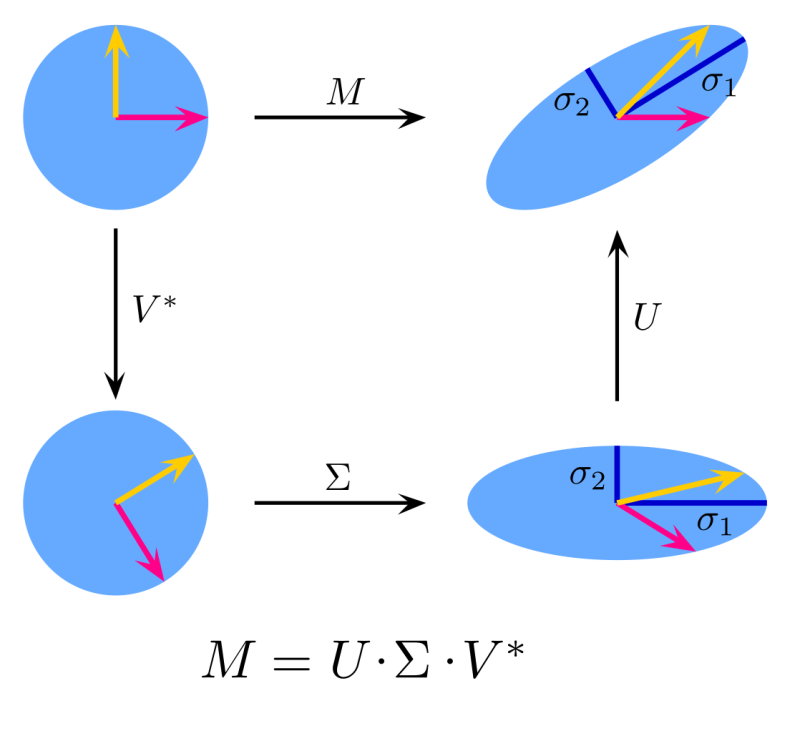
SVD is useful when there are a small number of concepts that connect the rows and columns of the original matrix. For example, if the original matrix represents the ratings given by movie viewers (rows) to movies (columns), the concepts might be the genres of the movies. The matrix U connects rows to concepts, Σ represents the strengths of the concepts, and V connects the concepts to columns.
In a complete SVD for a matrix, U and V are typically as large as the original. To use fewer columns for U and V, delete the columns corresponding to the smallest singular values from U, V and Σ. This choice minimizes the error in reconstructing the original matrix from the modified U, Σ and V.
Here is a notebook with sample implementations of Dimensionality Reduction.
Conclusion
Overall, these are the most interesting techniques that have been developed for efficient processing of large amounts of data in order to extract simple and useful models of that data. These techniques are often used to predict properties of future instances of the same sort of data, or simply to make sense of the data already available. Many people view data mining, or big data, as machine learning. There are indeed some techniques for processing large datasets that can be considered machine learning. But there are also many algorithms and ideas for dealing with big data that are not usually classified as machine learning, as shown here.
P.S: You can get all the lecture slides and quizzes from Mining of Massive Datasets from my GitHub repo here. Enjoy studying!





