Guide to Dijkstra’s Algorithm in Python

Dijkstra’s algorithm is a well-known algorithm in computer science that is used to find the shortest path between one vertex (source node) and all other vertices in a weighted graph. The algorithm uses a priority queue to explore the graph, assigning each vertex a tentative distance from a source vertex and then iteratively updating this value as it visits neighboring vertices.

We will go over how Dijkstra’s algorithm works, provide an example on a small graph, demonstrate its implementation in Python and touch on some of its practical applications.

How Dijkstra’s Algorithm Works

Dijkstra’s algorithm commonly works on directed graphs, where nodes are connected with weighted non-negative edges. In a directed graph, edges have specific, one-way directions for travel. The algorithm finds the distance from a single source node to all other nodes in the graph, where the sum of the edge weights on the paths is minimized. If we only care about the shortest distance to a single target node, we can simply stop the algorithm after that particular path has been found.

The time complexity of Dijkstra’s algorithm can be O(V^2) when using an array, or O((V + E) log V) when using a min-priority queue. In these equations, V represents the number of vertices and E represents the number of edges in the given graph. The space complexity of Dijkstra’s algorithm is typically O(V).

To initialize our graph, we first assign values to every node, which represents the node’s distance from the source. The source node receives a value of 0, the rest receive an initial (tentative) value of infinity ∞.

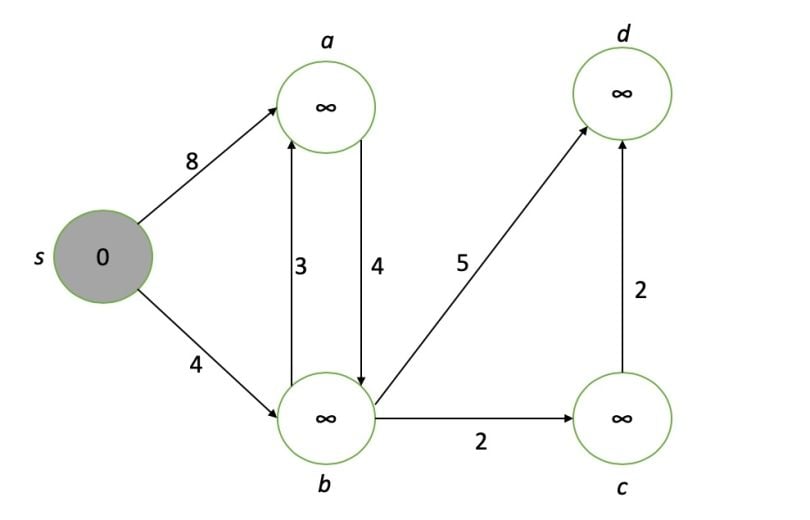
We will use this example graph where the source node is s, and there are four target nodes: a, b, c, and d.

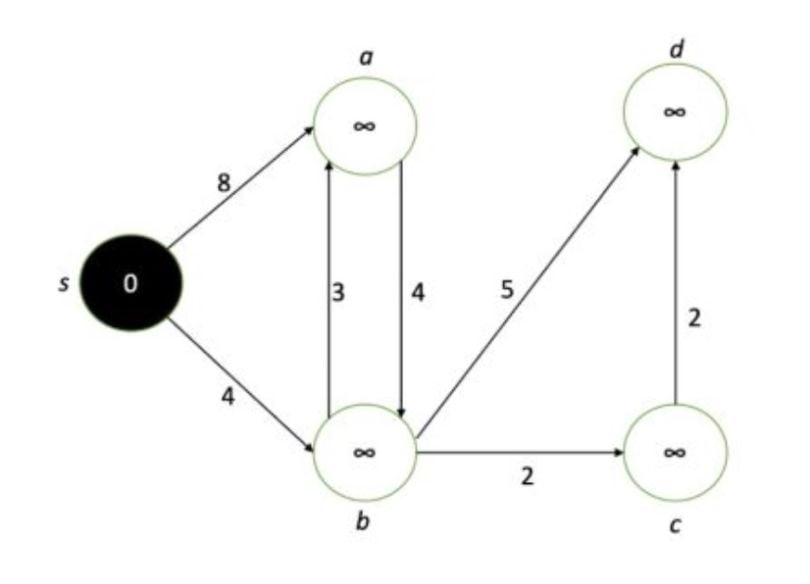
In the next step, we take the smallest-value unprocessed node (shaded gray). We then assign its value as the minimum of the current value, or any of the neighboring values plus the edge distance connecting them. In this first step, we assign s to min(0, ∞+4, ∞+8). So we keep the value as 0, then mark the node as completed (shaded with black).

Next, we take all our neighboring nodes and assign them again to the minimum of their current value, or their neighboring values plus the corresponding edge distances.

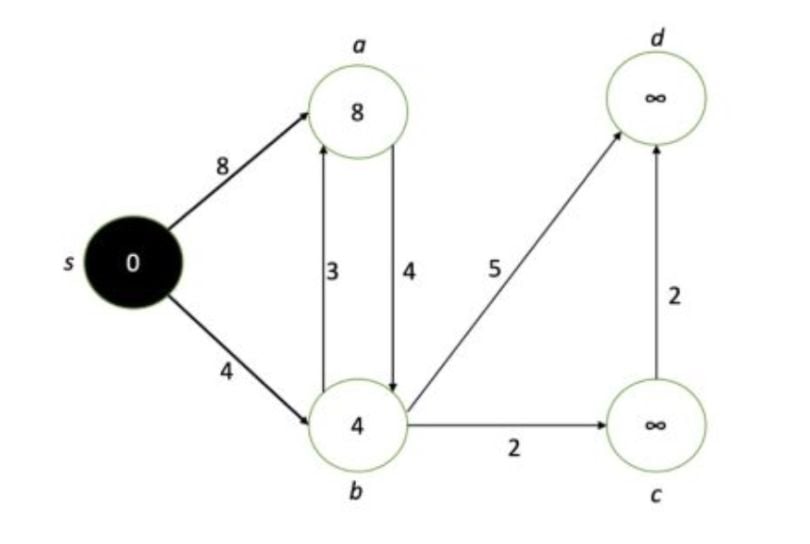
We take the smallest-valued node (b in this case) and treat it as our new node of interest.

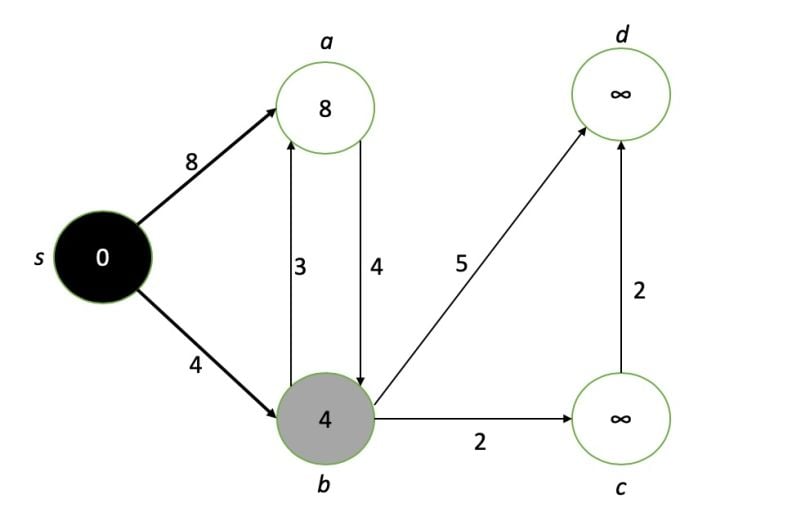
We then repeat the process with the next node: update its neighbors’ values, mark it as completed and find the next minimum-valued node.

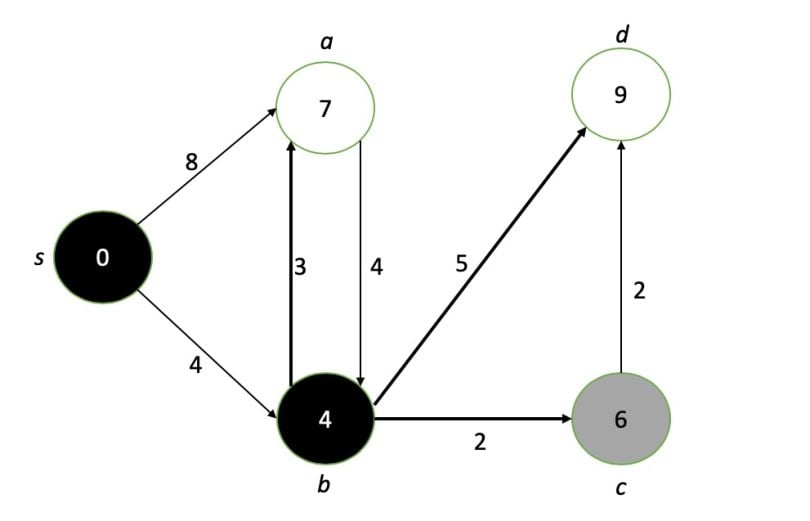
Note that once a node is marked as completed, its value is definitively the shortest path from the target. If this is the only node we care about, we can stop here. Or we can continue to find the shortest paths to all other nodes by repeating the process:

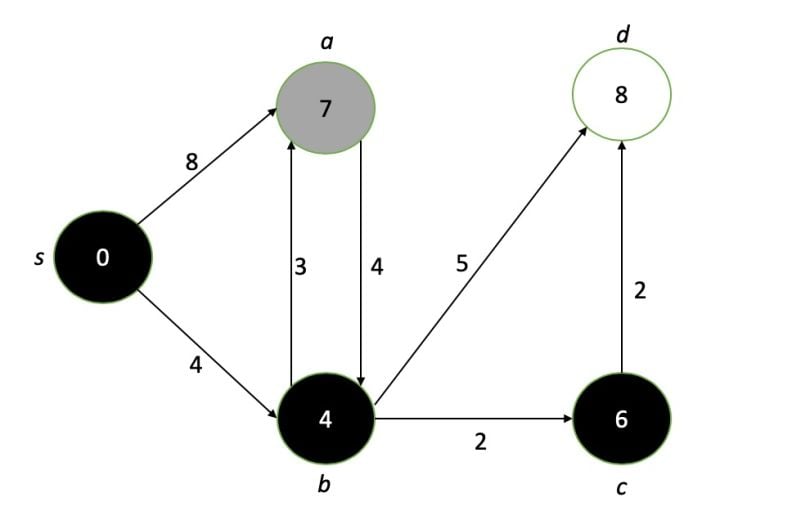
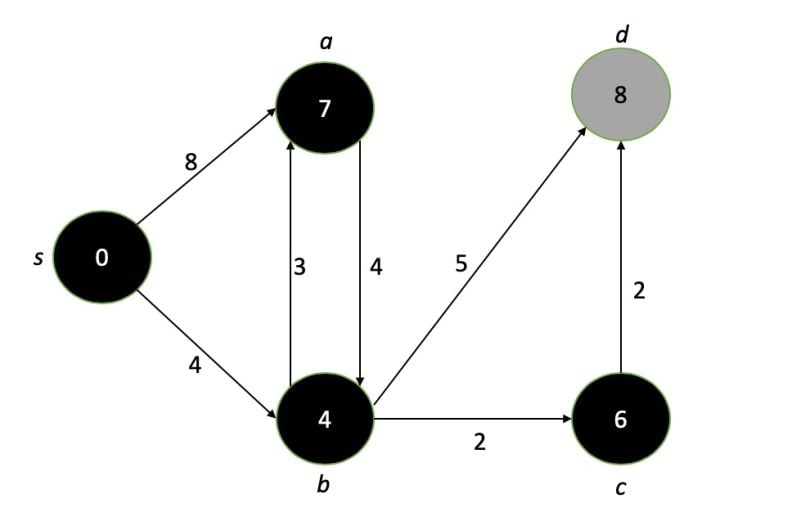
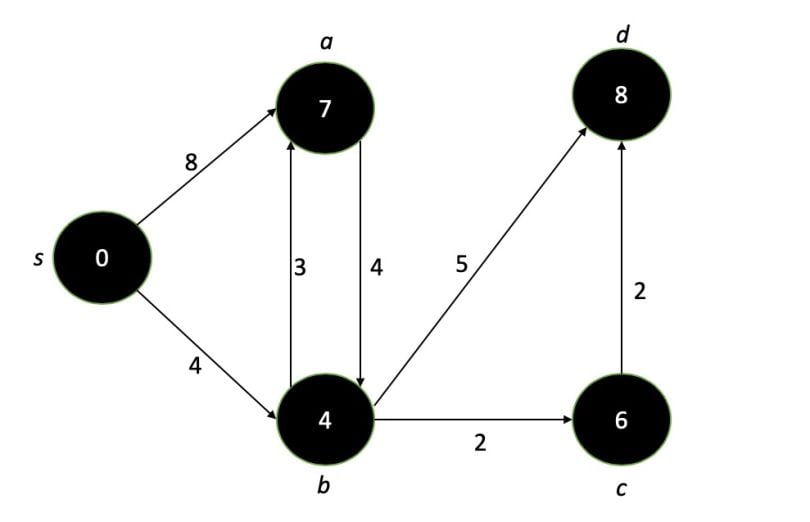
In summary, the steps are:

1. Initialize the source node to take value 0 and all other nodes to ∞. Start with node 0 as the “current node.” 
2. Find all neighboring nodes and update their values to either the minimum of their value or the value of the current node plus its distance. Mark the node as finished.
3. Assign the minimum-valued unfinished node as the current node.
4. Repeat steps 2 and 3 until all nodes (or a specific node of interest) are finished.

RelatedSorting Algorithms: Slowest to Fastest

Implementing Dijkstra’s Algorithm in Python

Implementing Dijkstra’s algorithm in Python is a good exercise for understanding how it works. We will cover the important components of a Python implementation. 

First, we can represent a directed graph using a dictionary adjacency list:

graph={
  's':{'a':8,'b':4},
  'a':{'b':4},
  'b':{'a':3,'c':2,'d':5},
  'c':{'d':2},
  'd':{}
}

class Node:
  def __init__(self,x_coord,y_coord):
      self.d=float('inf') #current distance from source node
      self.parent=None
      self.finished=False

def dijkstra(graph,source):
  nodes={}
  for node in graph:
      nodes[node]=Node()
  nodes[source].d=0
  queue=[(0,source)] #priority queue
  while queue:
      d,node=heapq.heappop(queue)
      if nodes[node].finished:
          continue
      nodes[node].finished=True
      for neighbor in graph[node]:
          if nodes[neighbor].finished:
              continue
          new_d=d+graph[node][neighbor]
          if new_d<nodes[neighbor].d:
              nodes[neighbor].d=new_d
              nodes[neighbor].parent=node
              heapq.heappush(queue,(new_d,neighbor))
  return nodes

There are a couple of important notes for this implementation. First, we keep the unfinished nodes in queue, using the built-in Python library heapq to push and pop nodes based on their distance value. Additionally, the returned value is a dictionary of nodes, where we can use the node’s parent, e.g. nodes['c'].parent to traverse the shortest path back to the source node.

RelatedBubble Sort Time Complexity and Algorithm Explained

Applications for Dijkstra’s Algorithm

Dijkstra’s algorithm can be used to find the shortest route between two points on a map, taking into account traffic conditions and other obstacles. In network routing, it can be used to find the shortest path between two computers on a network, while in computer networks, it can be used to find the fastest route between two nodes in a distributed system. 

It is also used in geographic information system (GIS) applications to find the shortest paths between geographic points. Generally, Dijkstra’s algorithm is a tool that has many real-world applications in various fields, particularly those that require efficient pathfinding in graph structures.

RelatedQuicksort Algorithm: An Overview

Dijkstra’s Algorithm vs. Other Shortest Path Algorithms

Dijkstra’s algorithm is one of several algorithms used to solve shortest path problems in graphs. In particular, Dijkstra’s algorithm is used to find a single-source shortest path in a weighted graph, where node edges are positive. Here are other shortest path algorithms to know and how they compare to Dijkstra’s algorithm:

• Bellman-Ford algorithm: Solves single-source shortest path problems in a weighted graph, where edges can be positive or negative (with no negative cycles).
• A* search algorithm: Solves single-pair shortest path problems in a weighted graph, where edges are positive.
• Floyd-Warshall algorithm: Solves all-pairs shortest path problems in a weighted graph, where edges can be positive or negative (with no negative cycles); effective for dense graphs (many edges).
• Johnson’s algorithm: Solves all-pairs shortest path problems in a weighted graph, where edges can be positive or negative (with no negative cycles); effective for sparse graphs (few edges).

Frequently Asked Questions