Graph Neural Network (GNN): What It Is and How to Use It

A graph neural network (GNN) is a form of neural network built to process and understand graph-structured data, or information that is represented within a graph data structure.

But first things first: What is a graph?

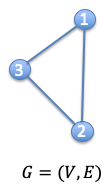
Graphs are mathematical data structures used to analyze the pair-wise relationship between objects and entities. A graph structure consists of two components: vertices, and edges. Typically, we define a graph as G=(V, E), where V is a set of nodes and E is the edge between them.

If a graph has N nodes, then adjacency matrix A has a dimension of (NxN). People sometimes provide another feature matrix to describe the nodes in the graph. If each node has F numbers of features, then the feature matrix X has a dimension of (NxF).

A graph doesn’t exist in a Euclidean space, which means it can’t be represented by any coordinate systems with which we’re familiar. This makes the interpretation of graph data much harder compared to other types of data like waves, images or time-series signals, all of which can be mapped to a 2-D or 3-D space.

Graphs also don’t have a fixed form. Look at the example below. Graphs A and B have completely different structures and look completely different from one another, but when we convert them to adjacency matrix representation, the two graphs have the same adjacency matrix (if we don’t consider the edges’ weight). So should we consider these two graphs to be the same or different from one another? It’s not always intuitive.

Finally, graphs are generally hard to visualize for human interpretation. I’m not talking about small graphs like the examples above, but about giant graphs that involve hundreds or thousands of nodes. When the dimension is very high and nodes are densely grouped, humans have a hard time understanding the graph. Therefore, it’s challenging for us to train a machine for this task. The example below shows a graph modeling the logic gates in an integrated circuit.

So why use graphs? A few reasons:

1. Graphs provide a better way of dealing with abstract concepts like relationships and interactions. They also offer an intuitive, visual way to think about these concepts. Graphs form a natural basis for analyzing relationships in a social context.
    
2. Graphs can solve complex problems by simplifying them visually or transforming problems into representations from different perspectives.
    
3. Graph theories and concepts are used to study and model social networks, fraud patterns, power consumption patterns, as well as virality and influence in social media. Social network analysis (SNA) is probably the best-known application of graph theory for data science.

Traditional Graph Analysis Methods

Traditional methods are mostly algorithm-based, such as:

1. Searching algorithms (e.g. breadth-first search [BFS], depth-first search [DFS].
    
2. Shortest path algorithms (e.g. Dijkstra’s algorithm, nearest neighbor).
    
3. Spanning-tree algorithms (e.g. Prim’s algorithm).
    
4. Clustering methods (e.g. highly connected components, k-mean).

The limitation of such algorithms is that we need to gain prior knowledge of the graph before we can apply the algorithm. Without prior knowledge, there’s no way to study the components of the graph itself and, more importantly, there’s no way to perform graph level classification.

Read More From Our ExpertsHow to Get Started With Social Network Analysis

What Is a Graph Neural Network (GNN)?

A graph neural network is a neural model that we can apply directly to graphs without prior knowledge of every component within the graph. GNN provides a convenient way for node level, edge level and graph level prediction tasks.

In GNNs, neighbors and connections define nodes. If we remove the neighbors and connections around a node, then the node will lose all its information. Therefore, the neighbors of a node and connections to neighbors define the concept of the node itself.

With this in mind, we give every node a state (x) to represent its concept. We can use the node state (x) to produce an output (o) (i.e. decision about the concept). We call the final state (x_n) of the node embedding. The task of all GNN is to determine the node embedding for each node by looking at the information on its neighboring nodes.

Types of Graph Neural Networks 

Graph neural networks have various types that excel in different areas. These include recurrent graph neural networks, graph convolutional networks and gated graph neural networks.

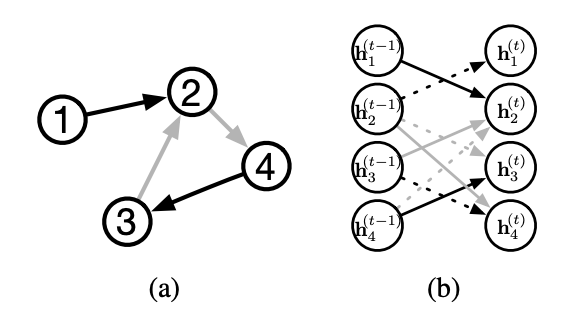
RECURRENT GRAPH NEURAL NETWORK (RecGNN or RGNN)

RecGNN is built with an assumption of Banach Fixed-Point Theorem. Banach Fixed-Point Theorem states:

Let (X,d) be a complete metric space and let (T:X→X) be a contraction mapping. Then T has a unique fixed point (x∗) and for any x∈X the sequence T_n(x) for n→∞ converges to (x∗).

This means if I apply the mapping T on x for k times, x^k should be almost equal to x^(k-1).

  RecGNN defines a parameterized function f_w:

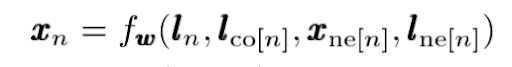
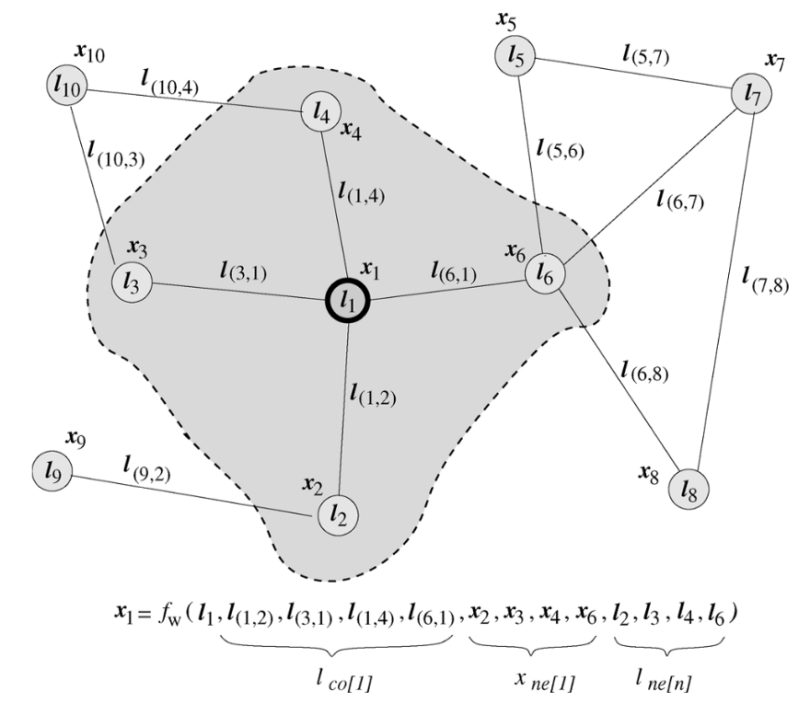
Here l_n, l_co, x_ne, l_ne represents the features of the current node [n], the edges of the node [n], the state of the neighboring nodes, and the features of the neighboring nodes.

Finally, after k iterations, the graph neural network model makes use of the final node state to produce an output in order to make a decision about each node. The output function is defined as:

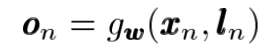
Graph CONVOLUTIONAL NETWORK (GCN)

Graph convolutional networks (GCNs) are one of the most popular types of GNNs. They function similarly to convolutional neural networks (CNNs), which makes them useful for image classification and segmentation tasks. The two main types of GCN algorithms include spatial graph convolutional networks and spectral graph convolutional networks.

Spatial Graph Convolutional Network (SGCN)

Spatial graph convolutional networks adopt the same mechanisms as convolutional neural networks by aggregating the features of neighboring nodes into the center node. In short, the idea of convolution on an image is to sum the neighboring pixels around a center pixel, specified by a filter with parameterized size and learnable weight. SGCNs carry this out but for data structured within a graph.

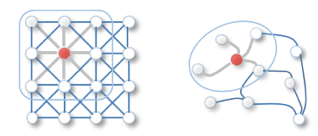
Spectral Graph Convolutional Network

Spectral graph convolutional networks have a strong mathematical foundation in comparison to other GNNs. Spectral convolutional network is built on graph signal processing theory as well as by simplification and approximation of graph convolution. Graph convolution can be simplified to this form:

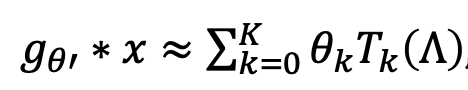
After further simplification Kipf and Welling suggest a two-layered neural network structure, described as:

Here A_head is the pre-processed Laplacian of the original graph adjacency matrix A. This formula looks very familiar if you have some experience in machine learning because it’s nothing but two fully connected layer structures that programmers commonly use. Nevertheless, it serves as graph convolution in this case.

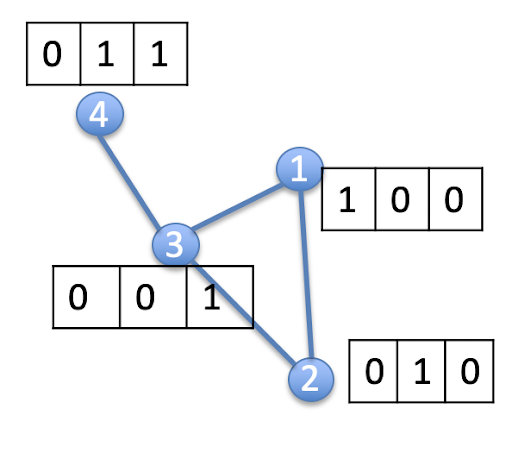
Let’s say we have a simple graph with four nodes. We assign each of these nodes a feature matrix as shown in the figure above. It’s easy to come out with a graph adjacency matrix and feature matrix.

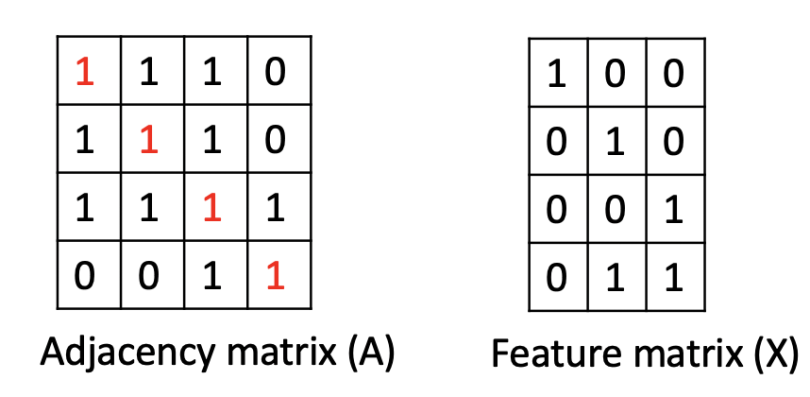
Note: I’ve purposely changed the diagonal of the adjacency matrix to 1 to add a self-loop for every node. This is so that we include the feature of every node itself when we perform feature aggregation later.

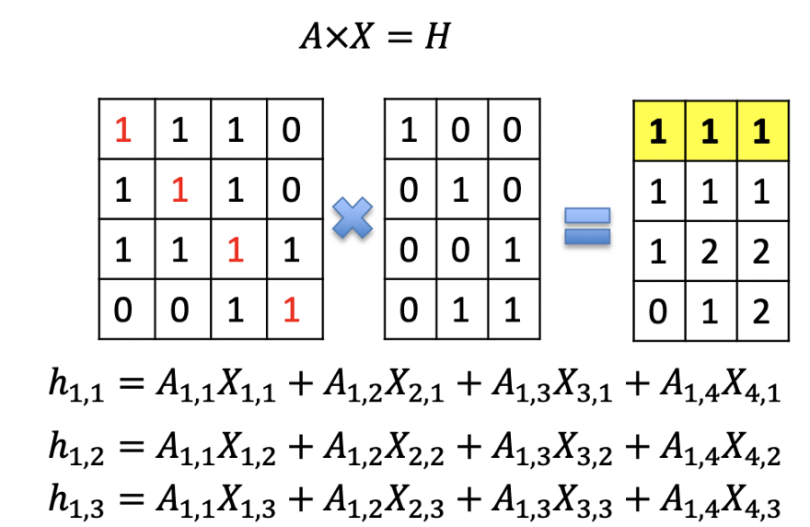
We then perform AxX (for our current purposes, let’s forget about the Laplacian of A and the weight matrix W). In the right-hand matrix, we see the result of matrix multiplication. Let’s look at the resulting feature of the first node as an example. It’s not hard to see the result is a sum of all features of node 1 including the feature of node 1 itself. Features in node 4 are not included since it’s not node 1’s neighbor. Mathematically, the graph’s adjacency matrix has a value of 1 only when there is an edge; otherwise it’s zero. This turns the matrix multiplication into the summation of nodes connected to the reference node.

Although spectral convolutional networks and spatial convolutional networks have different starting points, they share the same propagation rule. All convolutional graph neural networks currently available share the same format. They all try to learn a function to pass the node information around and update the node state through this message-passing process. Any graph neural network can be expressed as a message-passing neural network with a message-passing function, a node update function and a readout function.

Gated Graph Neural Network (GG-NN)

Gated graph neural networks are graph neural networks that are modified to use gated recurrent units (GRUs) and updated optimization techniques, which extend to model output sequences. Backpropagation through time is also used by GG-NNs to compute gradients. These features make GG-NNs suitable for non-sequential outputs and for applying long short-term memory (LSTM)-like inductive biases to solve graph-structured tasks.

What Are Graph Neural Networks Used For?

Node Classification

In node classification, the task is to predict the node embedding for every node in a graph. This type of problem is usually trained in a semi-supervised way, where only part of the graph has a label. Typical applications for node classification include citation networks, Reddit posts, YouTube videos and Facebook friendships.

Link Prediction

In link prediction, the task is to understand the relationship between entities in graphs and predict if two entities have a connection. For example, a recommender system can be treated as a link prediction problem. When we give the model a set of users’ reviews of different products, the task is to predict the users’ preferences and tune the recommender system to push more relevant products according to users’ interest.

Graph Classification

In graph classification, the task is to classify the whole graph into different categories. It’s similar to image classification, but the target changes into graph domain. There’s a wide range of industrial problems where graph classification can be applied; for example, in chemistry, biomedicine or physics, we can give the model a molecular structure and ask the model to classify the target into meaningful categories. The model then accelerates the analysis of atom, molecule or any other structured data types.

Graph Neural Network Applications

NATURAL LANGUAGE PROCESSING (NLP)

We often use GNN in natural language processing (NLP), which is where GNN got started. If you have experience with NLP, you must be thinking that text should be a type of sequential or temporal data, which we can describe with a recurrent neural network (RNN) or a long short-term memory (LTSM). Well, GNN approaches the problem from a completely different angle. GNN utilizes the inner relations of words or documents to predict categories. For example, a citation network tries to predict each paper’s label in a network by the paper citation relationship and the words cited in other papers. GNN can also build a syntactic model by looking at different parts of sentences instead of only working sequentially as in RNN or LSTM.

COMPUTER VISION

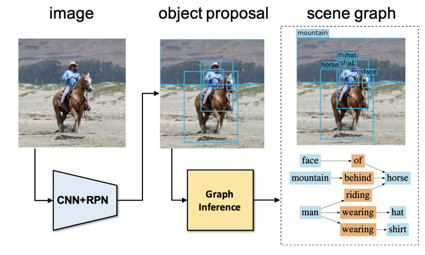
Many GNN-based methods have achieved state-of-the-art performance of object detections in images, yet we still don’t know the relationships between the objects. One successful employment of GNN in computer vision (CV) is using graphs to model relationships between objects detected by a CNN-based detector. After objects are detected from the images, they’re fed into a GNN inference for relationship prediction. The outcome of the GNN inference is a generated graph that models the relationships between different objects.

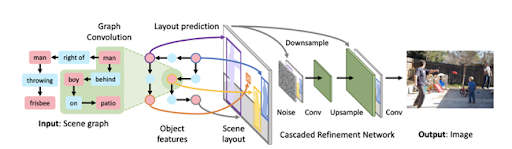
Another interesting application in CV is image generation from graph descriptions. We can interpret this as almost the reverse of the application above. The traditional way to perform image generation is text-to-image generation using generative adversarial network (GAN) or autoencoder. Instead of using text for image description, graph-to-image generation provides more information on the semantic structures of the images.

The most interesting application is zero-shot learning (ZSL), which learns to classify an object with no training samples of the target classes. If we provide no training samples we need to let the model think in order to recognize a target. For example, let’s say we’re given three images and told to find okapi among them. We may not have seen an okapi before, but if we’re also told an okapi is a deer-faced animal with four legs and zebra-striped skin, then it’s not hard for us to figure out which one is an okapi. Typical methods simulate this thinking process by converting the detected features into text. However, text encodings are independent among each other. It’s hard to model the relationships between the text descriptions. On the other hand, graph representations model these relationships well and help the machine think more like a human might.

GNN in Other Domains

More practical applications of GNN include human behavior detection, traffic control, molecular structure study, recommender systems, program verification, logical reasoning, social influence prediction and adversarial attack prevention. For example, GNN can be applied to cluster people into different community groups through social network analysis.

GNN is still a relatively new area and worthy of more research attention. It’s a powerful tool to analyze graph data because it’s not limited to problems in graphs. Graph modeling is a natural way to analyze a problem and GNN can easily be generalized to any study modeled by graphs.

Frequently Asked Questions