In order to understand the importance of activation functions, we first have to understand how a neural network computes a prediction/output, which we generally refer to as forward propagation. During forward propagation, the neural network receives an input vector x and outputs a prediction vector y.
What does that look like?
Consider the following neural network with one input, one output, and three hidden layers:

Each layer of the network is connected via a so-called weight matrix with the next layer. In total, we have 4 weight matrices W1, W2, W3, and W4.
Given an input vector x, we compute a dot-product with the first weight matrix W1 and apply the activation function to the result of this dot-product. The result is a new vector h1, which represents the values of the neurons in the first layer. We use this vector h1 as a new input vector for the next layer, where the same operations are performed again. We repeat this until we get the final output vector y, which is considered the neural network’s prediction.
These equations can represent the entire set of operations where σ represents an arbitrary activation function:
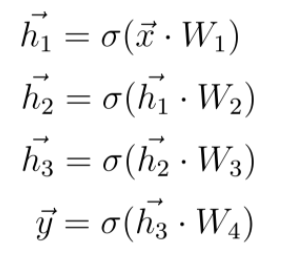
5 Deep Learning Activation Functions You Need to Know
- Sigmoid Activation Function
- Tanh Activation Function
- Rectified Linear Unit (ReLU) Activation Function
- Leaky ReLU Activation Function
- Softmax Activation Function
Neural Network as a Function
At this point, I’d like to discuss another interpretation we can use to describe a neural network. Rather than considering a neural network a collection of nodes and edges, we can simply call it a function.
Just like any regular mathematical function a neural network maps from input x to output y.
The concept of calculating an output y for an input x a common mathematical function f(x), which we define as follows:
This function takes three inputs x1, x2 and x3. a, b, c as the function parameters that take certain values. Given the input x1, x2 and x3, the function calculates an output y.
On a basic level, this is exactly how a neural network works. We take a feature vector x and put it into the neural network which calculates an output y.
We are trying to build a function that can model our training data.
That is, instead of considering a neural network as a simple collection of nodes and connections, we can think of a neural network as a function. This function incorporates all calculations that we’ve viewed separately as one single, chained calculation:
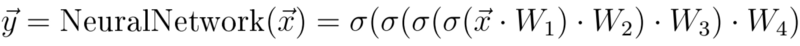
In the example above, the simple mathematical function we considered had the parameters a, b and c, which could strongly determine the output value of y for an input x.
In the case of a neural network, the parameters of the corresponding function are the weights. This means that our goal during the training of a neural network is to find a particular set of weights or parameters so that given the feature vector x we can calculate a prediction y that corresponds to the actual target value y_hat.
In other words, we are trying to build a function that can model our training data.
One question you might ask yourself is, can we always model the data? Can we always find weights that define a function that can compute a particular prediction y for given features x? The answer is no. We can only model the data if there is a mathematical dependency between the features x and the label y.
This mathematical dependence can vary in complexity. In most cases, we as humans can never see that relationship when we look at the data. However, if there is some sort of mathematical dependency between the features and labels, we can be sure that during the neural network training, the network will recognize this dependence and adjust its weights so it can model this dependence in the training data. Put another way, the network will realize a mathematical mapping from input features x to output y.
Why Do We Need Activation Functions?
The purpose of an activation function is to add some kind of non-linear property to the function, which is a neural network. Without the activation functions, the neural network could perform only linear mappings from inputs x to the outputs y. Why is this?
Without the activation functions, the only mathematical operation during the forward propagation would be dot-products between an input vector and a weight matrix.
A neural network without any activation function would not be able to realize such complex mappings mathematically and would not be able to solve tasks we want the network to solve.
Since a single dot product is a linear operation, successive dot products would be nothing more than multiple linear operations repeated one after the other. And successive linear operations can be considered as a single linear operation.
In order to compute really interesting stuff, neural networks must be able to approximate non-linear relations from input features to output labels. Usually, the more complex the data from which we are trying to learn something, the more non-linear the mapping of features to the ground-truth-label is.
A neural network without any activation function would not be able to realize such complex mappings mathematically and would not be able to solve tasks we want the network to solve.
5 Different Kinds of Activation Functions
At this point, we should discuss the different activation functions we use in deep learning as well as their advantages and disadvantages
1. Sigmoid Activation Function
Some years ago the most common activation function you would have encountered is the sigmoid function. The sigmoid function maps the incoming inputs to a range between zero and one:
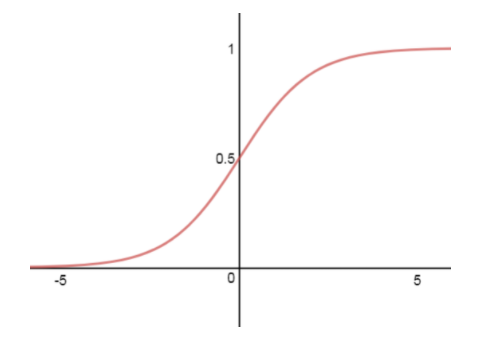
The sigmoid activation function is defined as follows:
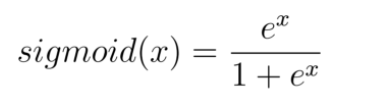
In practice, the sigmoid nonlinearity has recently fallen out of favor and we rarely ever use it anymore because it has two major drawbacks:
Sigmoid Kills Gradients
An undesirable feature of the sigmoid is the activation of the neurons saturates either at the tail of zero or one:
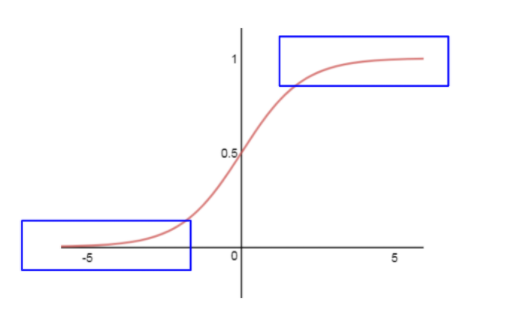
The derivative of the sigmoid function gets very small for these blue areas (meaning: large negative or positive input values). In this case, the near-zero derivative would make the gradient of the loss function very small, which prevents the update to the weights and thus the entire learning process.
Sigmoid Is Non-Zero Centered
Another undesirable property of the sigmoid activation is the fact the outputs of the function are not zero-centered. Usually, this makes training the neural network more difficult and unstable.
Consider a sigmoid neuron y with inputs x1 and x2 weighted by w1 and w2:
x1 and x2 are outputs of a previous hidden layer with sigmoid activation. So x1 and x2 are always positive since the sigmoid is not zero-centered. Depending on the gradient of the whole expression y=x1*w1+x2*w2 the gradient with respect to w1 and w2 will always be either positive for w1 and w2 or negative for w1 and w2.
Often the optimal gradient descent step requires an increase of w1 and a decrease of w2. So since x1 and x2 are always positive we can’t increase and decrease the weights at the same time, but can only increase or decrease all weight at the same time. So, in the end, we will require more steps.
2. Tanh Activation Function
Another common activation function used in deep learning is the tanh function. We can see the tangens hyperbolicus non-linearity here:

The function maps a real-valued number to the range [-1, 1] according to the following equation:
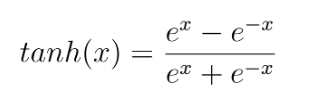
As with the sigmoid function, the neurons saturate for large negative and positive values, and the derivative of the function goes to zero (blue area). But unlike the sigmoid its outputs are zero-centered.
Therefore, in practice, the tanh non-linearity is always preferred to the sigmoid non-linearity.
3. Rectified Linear Unit (ReLu) Activation Function
The Rectified Linear Unit (ReLU) has become very popular in the last few years. The activation is simply thresholded at zero: R(x) = max(0,x) or more precisely:
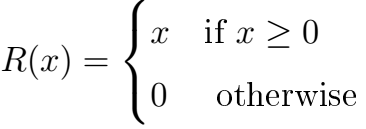
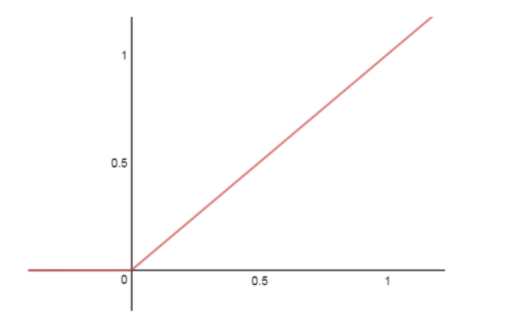
There are several pros and cons of using ReLUs:
-
PRO: In practice, ReLU accelerates the convergence of gradient descent towards the global minimum of the loss function in comparison to other activation functions. This is due to its linear, non-saturating property.
-
PRO: While other activation functions (tanh and sigmoid) involve very computationally expensive operations such as exponentials etc., we can easily implement ReLU by simply thresholding a vector of values at zero.
-
CON: There is unfortunately also a problem with the ReLU activation function. Because the outputs of this function are zero for input values that are below zero, the network neurons can be very fragile during training and can even die. What does this mean? It can (doesn't have to but can) happen that during the weight updates the weights are adjusted in such a way that for certain neurons the inputs are always below zero. This means that the hidden values of these neurons are always zero and do not contribute to the training process. This means that the gradient flowing through these ReLU neurons will also be zero from that point on. We say that the neurons are dead. For example, it’s common to observe that as much as 20-50 percent of the entire neural network that used ReLU activation can be dead. In other words, these neurons will never activate in the data set used during training.
4. Leaky ReLU Activation Function
Leaky ReLu is nothing more than an improved version of the ReLU activation function. As IU mentioned above, it’s common that, by using ReLU, we may kill some neurons in our neural network and these neurons will never activate on any data again.
Leaky ReLU was defined to address this problem. In contrast to regular ReLU where all outputs are zero for input values below zero, with leaky ReLU we add a small linear component to the function:
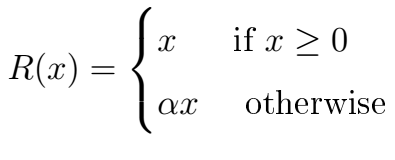
The leaky ReLU activation looks like this:
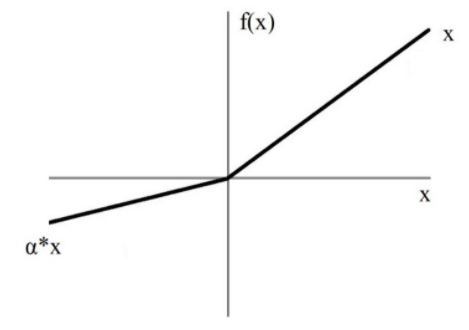
Basically, we’ve replaced the horizontal line for values below zero with a non-horizontal, linear line. The slope of this linear line can be adjusted by the parameter α that we multiply with the input x.
The advantage to using leaky ReLU and replacing the horizontal line is that we avoid zero-gradients. This is because we no longer have dead neurons that are always zero, thereby causing our gradient to become zero.
5. Softmax Activation Function
Last but not least, I would like to introduce the softmax activation function. This activation function is quite unique.
We apply softmax in the last layer and only when we want the neural network to predict probability scores during classification tasks.
Simply speaking, the softmax activation function forces the values of output neurons to take values between zero and one, so they can represent probability scores.
Another thing we must consider is that when we perform the classification of input features into different classes, these classes are mutually exclusive. This means that each feature vector x belongs to only one class. For example, a feature vector that is an image of a dog can’t represent a dog class with a probability of 50 percent and a cat class with a probability of 50 percent. This feature vector must represent the dog class with a probability of 100 percent
In the case of mutually exclusive classes, the probability scores across all output neurons must sum up to one. Only in this way the neural network represents a proper probability distribution. A counterexample would be a neural network that classifies a dog’s image into the class dog with a probability of 80 percent and with a class cat probability of 60 percent.
In the case of mutually exclusive classes, the probability scores across all output neurons must sum up to one.
Fortunately, the softmax function does not only force the outputs into the range between zero and out, but the function also makes sure that the outputs across all possible classes sum up to one. Let's now see how the softmax function works in practice.
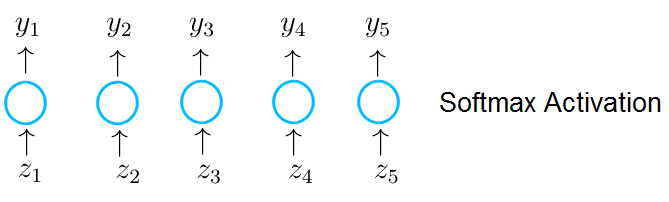
Imagine that the neurons in the output layer receive an input vector z, which is the result of a dot-product between a weight matrix of the current layer with the output of a previous layer. A neuron in the output layer with a softmax activation receives a single value z1, which is an entry in the vector z and outputs the value y_1.
When we use softmax activation every single output of a neuron in the output layer is computed according to the following equation:
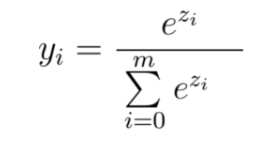
As you can see each value y of a particular neuron does not only depend on the value z which the neuron receives but on all values in the vector z. This makes each value y of an output neuron a probability value between zero and one. And the probability predictions across all output neurons sum up to one.
The output neurons now represent a probability distribution over the mutually exclusive class labels.
What Activation Function Should I Use?
I will answer this question with the best answer there is: it depends.
Which Activation Function Should You Use? Some Tips.
- Activation functions add a non-linear property to the neural network, which allows the network to model more complex data.
- In general, you should use ReLU as an activation function in the hidden layers.
- Regarding the output layer, we must always consider the expected value range of the predictions.
- For classification tasks, I recommend exclusively using the softmax activation in the output layer exclusively.
Specifically, it depends on the problem you are trying to solve and the value range of the output you’re expecting.
For example, if you want your neural network to predict values that are larger than one, then tanh or sigmoid is not suitable for use in the output layer, and we must use ReLU instead.
On the other hand, if we expect the output values to be in the range [0,1] or [-1, 1] then ReLU is not a good choice for the output layer and we must use sigmoid or tanh.
If you perform a classification task and want the neural network to predict a probability distribution over the mutually exclusive class labels, then you should use the softmax activation function in the last layer.
However, regarding the hidden layers, as a rule of thumb, I would strongly suggest you always use ReLU as an activation for these layers.
So long as you choose the right activation function for your project, you’ll be well on your way to having an efficient neural network that can model complex data.