C-Means Clustering Explained

Clustering is an unsupervised machine learning technique that divides the population into several groups or clusters such that data points in the same group are similar to each other, and data points in different groups are dissimilar.

What Is C-Means Clustering?

C-means clustering, or fuzzy c-means clustering, is a soft clustering technique in machine learning in which each data point is separated into different clusters and then assigned a probability score for being in that cluster. Fuzzy c-means clustering gives better results for overlapped data sets compared to k-means clustering.

In other words, clusters are formed in a way that:

Data points in the same cluster are close to each other and are very similar
Data points in different clusters are far apart and are different from each other.

Clustering is used to identify some segments or groups in your dataset. Clustering can be divided into two sub-groups:

Clustering flow chart divided into hard clustering and soft clustering — Subgroups of clustering. | Image: Satyam Kumar

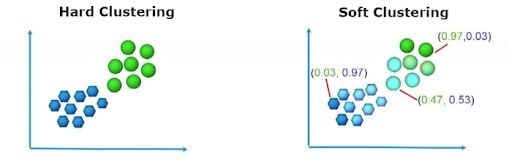
Charts showing difference between hard and soft clustering data sets — Examples of hard clustering (left) and soft clustering (right) data sets. | Image: Satyam Kumar

What Is Hard Clustering?

In hard clustering, each data point is clustered or grouped to any one cluster. For each data point, it may either completely belong to a cluster or not. As observed in the above diagram, the data points are divided into two clusters, each point belonging to either of the two clusters.

K-means clustering is a hard clustering algorithm. It clusters data points into k-clusters.

More on Data ScienceK-Nearest Neighbor Algorithm: An Introduction

What Is Soft Clustering?

In soft clustering, instead of putting each data point into separate clusters, a probability of that point is assigned to probable clusters. In soft clustering or fuzzy clustering, each data point can belong to multiple clusters along with its probability score or likelihood.

One of the widely used soft clustering algorithms is the fuzzy c-means clustering (FCM) Algorithm.

How C-Means Clustering Works

Fuzzy c-means clustering is a soft clustering approach, where each data point is assigned a likelihood or probability score belonging to that cluster. The step-wise approach of the fuzzy c-means clustering algorithm is:

Fix the value of c (number of clusters), and select a value of m (generally 1.25<m<2), and initialize partition matrix U.

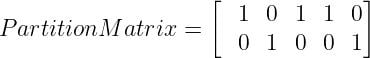
Calculate the cluster centers (centroid).

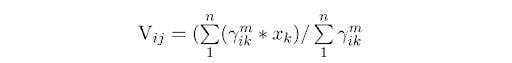
clusters centroid equation — Cluster centers equation. | Image: Satyam Kumar

Here:

µ: Fuzzy membership value
m: Fuzziness parameter

Update the partition matrix.

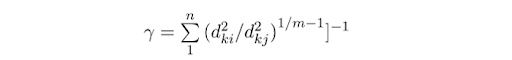
Repeat the above steps until convergence.

Tutorial on the basics of fuzzy c-means clustering. | Video: Data Science With Sharan

How to Install and Use the C-Means Algorithm

To implement the fuzzy c-means algorithm, we can use an open-sourced Python package that can be installed through PyPI:

pip install fuzzy-c-means

Fuzzy c-means is a Python module that can implement the fuzzy c-means algorithm. This module has an API similar to that of Scikit-learn.

!pip install fuzzy-c-means
Collecting fuzzy-c-means
  Downloading https://files.pythonhosted.org/packages/cc/34/64498f52ddfb0a22a22f2cfcc0b293c6864f6fcc664a53b4cce9302b59fc/fuzzy_c_means-1.2.4-py3-none-any.whl
Requirement already satisfied: jaxlib<0.2.0,>=0.1.57 in /usr/local/lib/python3.7/dist-packages (from fuzzy-c-means) (0.1.64+cuda110)
Requirement already satisfied: jax<0.3.0,>=0.2.7 in /usr/local/lib/python3.7/dist-packages (from fuzzy-c-means) (0.2.11)
Requirement already satisfied: numpy>=1.16 in /usr/local/lib/python3.7/dist-packages (from jaxlib<0.2.0,>=0.1.57->fuzzy-c-means) (1.19.5)
Requirement already satisfied: scipy in /usr/local/lib/python3.7/dist-packages (from jaxlib<0.2.0,>=0.1.57->fuzzy-c-means) (1.4.1)
Requirement already satisfied: flatbuffers in /usr/local/lib/python3.7/dist-packages (from jaxlib<0.2.0,>=0.1.57->fuzzy-c-means) (1.12)
Requirement already satisfied: absl-py in /usr/local/lib/python3.7/dist-packages (from jaxlib<0.2.0,>=0.1.57->fuzzy-c-means) (0.12.0)
Requirement already satisfied: opt-einsum in /usr/local/lib/python3.7/dist-packages (from jax<0.3.0,>=0.2.7->fuzzy-c-means) (3.3.0)
Requirement already satisfied: six in /usr/local/lib/python3.7/dist-packages (from absl-py->jaxlib<0.2.0,>=0.1.57->fuzzy-c-means) (1.15.0)
Installing collected packages: fuzzy-c-means
Successfully installed fuzzy-c-means-1.2.4
import numpy as np
from fcmeans import FCM
from matplotlib import pyplot as plt
n_samples = 5000

X = np.concatenate((
    np.random.normal((-2, -2), size=(n_samples, 2)),
    np.random.normal((2, 2), size=(n_samples, 2))
))
fcm = FCM(n_clusters=2)
fcm.fit(X)
# outputs
fcm_centers = fcm.centers
fcm_labels = fcm.predict(X)

# plot result
f, axes = plt.subplots(1, 2, figsize=(11,5))
axes[0].scatter(X[:,0], X[:,1], alpha=.1)
axes[1].scatter(X[:,0], X[:,1], c=fcm_labels, alpha=.1)
axes[1].scatter(fcm_centers[:,0], fcm_centers[:,1], marker="+", s=500, c='w')
plt.show()

More on PythonPIP Command Not Found: A Guide

C-Means Advantages

Fuzzy c-means clustering can be considered a better algorithm compared to the k-means algorithm. Unlike the k-means algorithm, where the data points exclusively belong to one cluster, data points in the fuzzy c-means algorithm can belong to more than one cluster with a likelihood. As a result, fuzzy c-means clustering gives comparatively better results for overlapped data sets.