SARSA Reinforcement Learning Algorithm: A Guide

State-action-reward-state-action (SARSA) is an on-policy algorithm designed to teach a machine learning model a new Markov decision process policy in order to solve reinforcement learning challenges. It’s an algorithm where, in the current state (S), an action (A) is taken and the agent gets a reward (R), and ends up in the next state (S1), and takes action (A1) in S1. Therefore, the tuple (S, A, R, S1, A1) stands for the acronym SARSA. 

It’s called an on-policy algorithm because it updates the policy based on actions taken.

SARSA Algorithm 

The algorithm for SARSA is a little bit different from Q-learning.

In the SARSA algorithm, the Q-value is updated taking into account the action, A1, performed in the state, S1. In Q-learning, the action with the highest Q-value in the next state, S1, is used to update the Q-table.

More on Machine Learning: Markov Chain Explained

How Does the SARSA Algorithm Work? 

The SARSA algorithm works by carrying out actions based on rewards received from previous actions. To do this, SARSA stores a table of state (S)-action (A) estimate pairs for each Q-value. This table is known as a Q-table, while the state-action pairs are denoted as Q(S, A). 

The SARSA process starts by initializing Q(S, A) to arbitrary values. In this step, the initial current state (S) is set, and the initial action (A) is selected by using an epsilon-greedy algorithm policy based on current Q-values. An epsilon-greedy policy balances the use of exploitation and exploration methods in the learning process to select the action with the highest estimated reward. 

Exploitation involves using already known, estimated values to get more previously earned rewards in the learning process. Exploration involves attempting to find new knowledge on actions, which may result in short-term, sub-optimal actions during learning but may yield long-term benefits to find the best possible action and reward.

From here, the selected action is taken, and the reward (R) and next state (S1) are observed. Q(S, A) is then updated, and the next action (A1) is selected based on the updated Q-values. Action-value estimates of a state are also updated for each current action-state pair present, which estimates the value of receiving a reward for taking a given action.

The above steps of R through A1 are repeated until the algorithm’s given episode ends, which describes the sequence of states, actions and rewards taken until the final (terminal) state is reached. State, action and reward experiences in the SARSA process are used to update Q(S, A) values for each iteration.

SARSA vs. Q-learning

The main difference between SARSA and Q-learning is that SARSA is an on-policy learning algorithm, while Q-learning is an off-policy learning algorithm. 

In reinforcement learning, two different policies are also used for active agents: a behavior policy and a target policy. A behavior policy is used to decide actions in a given state (what behavior the agent is currently using to interact with its environment), while a target policy is used to learn about desired actions and what rewards are received (the ideal policy the agent seeks to use to interact with its environment).

If an algorithm’s behavior policy matches its target policy, this means it is an on-policy algorithm. If these policies in an algorithm don’t match, then it is an off-policy algorithm. 

SARSA operates by choosing an action following the current epsilon-greedy policy and updates its Q-values accordingly. On-policy algorithms like SARSA select random actions where non-greedy actions have some probability of being selected, providing a balance between exploitation and exploration techniques. Since SARSA Q-values are generally learned using the same epsilon-greedy policy for behavior and target, it classifies as on-policy.

Q-learning, unlike SARSA, tends to choose the greedy action in sequence. A greedy action is one that gives the maximum Q-value for the state, that is, it follows an optimal policy. Off-policy algorithms like Q-learning learn a target policy regardless of what actions are selected from exploration. Since Q-learning uses greedy actions, and can evaluate one behavior policy while following a separate target policy, it classifies as off-policy.

More on Machine Learning:  How Does Backpropagation in a Neural Network Work?

How to Use SARSA 

Now, let’s look at the code for SARSA to solve the FrozenLake environment:

import gym
import numpy as np
import time, pickle, os

env = gym.make('FrozenLake-v0')

epsilon = 0.9
# min_epsilon = 0.1
# max_epsilon = 1.0
# decay_rate = 0.01

total_episodes = 10000
max_steps = 100

lr_rate = 0.81
gamma = 0.96

Q = np.zeros((env.observation_space.n, env.action_space.n))
    
def choose_action(state):
	action=0
	if np.random.uniform(0, 1) < epsilon:
		action = env.action_space.sample()
	else:
		action = np.argmax(Q[state, :])
	return action

def learn(state, state2, reward, action, action2):
	predict = Q[state, action]
	target = reward + gamma * Q[state2, action2]
	Q[state, action] = Q[state, action] + lr_rate * (target - predict)

# Start
rewards=0

for episode in range(total_episodes):
	t = 0
	state = env.reset()
	action = choose_action(state)
    
	while t < max_steps:
		env.render()

		state2, reward, done, info = env.step(action)

		action2 = choose_action(state2)

		learn(state, state2, reward, action, action2)

		state = state2
		action = action2

		t += 1
		rewards+=1

		if done:
			break
  # epsilon = min_epsilon + (max_epsilon - min_epsilon) * np.exp(-decay_rate * episode) 
  # os.system('clear')
		time.sleep(0.1)

    
print ("Score over time: ", rewards/total_episodes)
print(Q)

with open("frozenLake_qTable_sarsa.pkl", 'wb') as f:
	pickle.dump(Q, f)

You’ll see that the code is similar to what’s used in Q-learning to solve the FrozenLake environment. 

Now, let’s dissect it.

On lines 38 and 39, an action is chosen for the initial state.

In the SARSA tuple, we now have:

                        (State, Action)

Then, this action is taken in the environment, and the reward and next state are observed on line 44.

Now, the tuple has:

               (State, Action, Reward, State1)

On line 46, an action is chosen for the next state using the choose_state(…) function.

The action chosen by the choose_action(…) function is done using the epsilon-greedy approach.

Now, the tuple is complete as:

           (State, Action, Reward, State1, Action1)

On line 48, the learn(…) function updates the Q-table using the following equation:

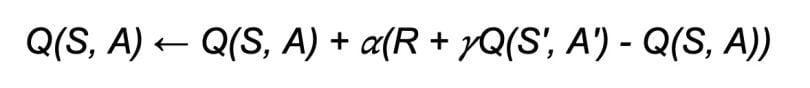
In the SARSA update equation, the Q-value is chosen using S’ and A’, the next state and the action chosen in the next state, respectively. This stands in contrast to Q-learning, which updates the equation where the max of Q(S’, a) is taken.

The rest of the code is similar to the Q-learning code.

Try to tweak the different parameters to get better results. 

Frequently Asked Questions