We often observe events unfolding in this pattern (extreme, typical, typical, extreme, and so on) because of a statistical phenomenon called regression to the mean or reversion to mediocrity. Regression to the mean refers to the idea that rare or extreme events are likely to be followed by more typical ones. Over time, outcomes “regress” to the average or “mean.”
How Regression to the Mean Works
Regression to the mean is a statistical phenomenon in which an extreme outcome is likely to revert back to average. This is often because the outlier experience involves a series of variables — either good or bad — occurring simultaneously to create a great or poor result, like flipping a coin and getting heads multiple times. This is why an extreme outcome is typically followed by an average result.
Below are some hypothetical statements you may have either read, heard or said in some variation. Can you spot anything wrong with them?
- A teacher laments: “When I praise my students for good work, the next time they try, they tend to be less good. When I punish my students for producing bad work, the next time they try, they tend to do much better. Therefore, punishments work but rewards do not.”
- An aspiring athlete marvels: “Wow, yesterday my foot was really painful, and I soaked it in a hot bowl of garlic-infused water, now it feels much better. There must be some healing properties in that garlicky water!”
- A film critic stipulates: “Winning an Academy Award, the most prestigious prize in show business, can lead an actor’s career to decline rather than ascend.”
Your hunch might be that there’s something fishy with these statements. Surely, garlicky water can’t cure a painful foot. This article explains why these statements are problematic through the concept of regression to the mean and suggests some steps you can take to avoid making this fallacy.
Regression to the Mean Defined
Let’s take a look at the pattern of events spoken about in these statements. In all these statements, events unfold as follows: an “extreme” event (either in a good or bad direction) is followed by a more typical one.
Regression to the mean was coined by Sir Francis Galton when he noticed that tall parents tend to have children who are shorter than them, whereas short parents often have children who are taller than them. Graphically, this means that if we plot the height of parents on the x-axis and the height of kids on the y-axis and draw a line through all the data points, we get a line with a slope of less than one, or equivalently an angle of less than 45 degrees.
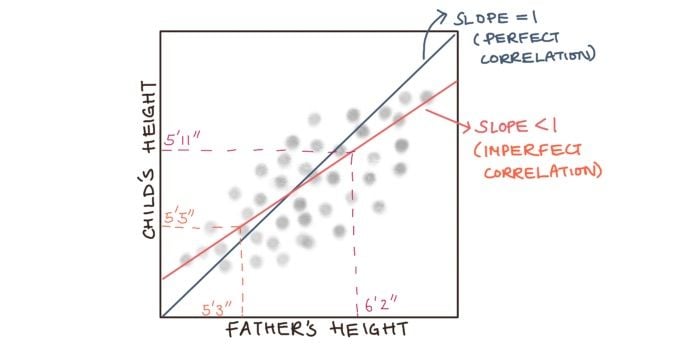
This diagram shows that a father who is taller than the average man in the population will, on average, have a son who is slightly shorter than him. A father who is shorter than the average man in the population will, on average, have a son who is slightly taller than him.
This concept is useful not just for looking at the relationship between the heights of parents and their offspring. If you reflect on your own experience, you’ll most likely find this phenomenon popping up everywhere. For example, regression to the mean explains why the second time you visit a restaurant you thought so highly of last time fails to live up to your expectations. Surely, it can’t just be you who thinks the creme brulee was better last time.
The statistical feature that explains such a phenomenon is that getting multiple extreme outcomes consecutively is like getting heads on a coin multiple times — unusual and difficult to repeat. The various factors that make a restaurant experience optimal, like the quality of food, how busy the restaurant is at the time of your visit, the friendliness of the waiter, your mood that day, are difficult to repeat exactly the second time around.
How Regression to the Mean Prevents False Assumptions
The general statistical rule is that whenever the correlation between two variables is imperfect, i.e. in the graph above, the slope is not one, there will be regression to the mean. But, so what?
Regression to the mean is a statistical fact about the world that is both easy to understand and easy to forget. Because the sequence of events unfolds extreme, typical, typical, extreme…, our brains automatically draw a relationship between the “extreme” event and the “typical” event. We erroneously infer that the extreme event caused the typical event. For example, winning an Oscar led to subsequent mediocre movies, or that something in between those two events caused the typical event, like in the case of the garlicky water healing the foot.
In short, when we forget the role of regression to the mean, we end up attributing certain outcomes to particular causes, such as people, prior events or interventions, when in fact these outcomes are most likely due to chance. In other words, the normal outcome would have occurred even if we removed the prior extreme outcomes that came before it.
Let’s recall the first three statements in this article. What does regression to the mean imply about the veracity of these statements?
The Teacher’s Mistake
The teacher suggests that rewarding their students makes them perform worse next time. But seen from the framework of regression to the mean, the teacher claims too much credit for their reward/punishment system.
As Daniel Kahneman notes in Thinking, Fast and Slow, Success = Talent + Luck. The luck component of this equation implies that a string of successes (or failures) are difficult to repeat, even if one has a lot of talent or no talent.
Consider two students, Jane and Joe. In year one, Jane does horribly but Joe is outstanding. Jane is ranked in the bottom 1 percent while Joe is ranked at the top 99 percent. If their results were entirely due to talent, there would be no regression. Jane should be as bad in year two, and Joe should be as good in year two. This is represented as possibility A in the diagram below. If their results were equal parts luck and talent, we would expect halfway regression: Jane should rise to around 25 percent and Joe should fall to around 75 percent, possibility B. If their results were caused entirely by luck (e.g. flipping a coin), then in year two we would expect both Jane and Joe to regress all the way back to 50 percent, possibility C.
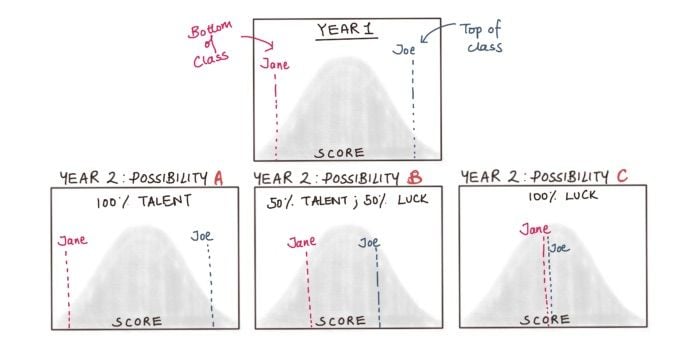
The Success = Talent + Luck equation means that the most likely scenario is some degree of regression. Jane who did awfully in the first year is likely to do somewhat better in the second year, regardless of whether she is punished, and Joe, who did extremely well in the first year, is likely to do somewhat worse in year two regardless of whether he is rewarded. The teacher’s punishment and reward system may not be as powerful as they think.
The Athlete’s Mistake
The athlete suggests that the garlicky water healed their painful foot. Suppose that the athlete’s foot was hurting really badly one day. In desperation, they try everything, including the garlic-infused water right before bed. They wake up and find that their foot feels a lot better. Perhaps the water does have some healing properties. But regression to the mean seems to be an equally plausible story.
Since physical maladies have a natural ebb and flow, a really painful day is likely to be followed by a less painful day. The pattern of how pain rises and falls might make it look as though the garlicky-water is an effective treatment. But it’s more likely that the garlicky-water didn’t do anything. The pain would subside anyway due to the natural course of biology.
This example shows how regression to the mean can often be used to make ineffective treatments look effective. A quack who sees their patient at their lowest point might offer an ineffective medicine, betting that their patient will be less sick the next day, and then infer that the medicine is what did the trick.
The Film Critic’s Mistake
The film critic alludes to the Oscar curse, which says that once you’ve won an Oscar, your next movie and performance aren’t going to be as good — it might even be bad. Several interviews with actors and actresses suggest that they also believe in the curse, saying that the pressure and expectation that comes with winning such a prestigious award ends up hurting their careers.
While pressure and expectations might explain the success, or lack thereof, of their next film, the “curse” could also be in large part due to regression to the mean. Actors sometimes have really good performances due to a combination of a good screenplay, a good director, good chemistry with other actors and a right fit for the part. Statistically speaking, the odds of all these factors coming together in the same dose and in the same way for their next movie project are low. So, it seems natural to expect their next performance to be worse than their Oscar-winning performance. The curse isn’t so mystical, after all.
Why Regression to the Mean Is Important
Regression to the mean describes the feature that extreme outcomes tend to be followed by more normal ones. It’s a statistical concept that is both easy to understand and easy to forget. When we witness extreme events, such as unlikely successes or failures, we forget how rare such events are. When these events are followed by more normal events, we try to explain why these “normal” events happened. We forget that these “normal” events are normal and that we should expect them to happen. This often leads us to attribute causal powers to people, events, and interventions that may have played no role in bringing about that normal event.
To avoid making this fallacy, we should first catch ourselves when we’re trying to explain some (either positive or negative) event or outcome. Then, we should ask ourselves the following questions:
- Is there anything abnormal about this outcome, or is this what you should expect, statistically speaking?
- Was this event preceded by an extreme outcome that makes the normal one look strange in comparison?
- Would the normal event have happened anyway, even if we removed the events before it? For example, would the athlete’s foot have felt better even if they didn’t soak it in garlicky water?
The first question forces us to consider the likelihood of the normal event happening. The second encourages us to think about outcomes in relation to each other, not as isolated observations. The third pushes us to engage in counterfactual thinking, imagining a world where the entity that we believe to have caused the normal event has been removed. By asking ourselves these three questions, we are less likely to ascribe unwarranted powers to events, people, systems and interventions.
