Dominated Strategy in Game Theory: Explained

A dominated strategy in game theory is one that results in a worse outcome for a player than another strategy they could choose, regardless of what the other players do.

The concept of equilibrium in dominant strategies can simplify decision-making. In the Prisoner’s Dilemma, once Player 1 identifies a dominant strategy, they no longer need to consider Player 2’s actions — playing the dominant strategy will always yield a better outcome. Even in games where all players have dominant strategies, the final outcome depends on the combination of those strategies, but each player’s best response remains fixed.

But what happens when not all players have dominant strategies — or none do at all? In these cases, identifying and eliminating dominated strategies can help simplify the game and narrow down the possible outcomes.

Dominated Strategy vs. Dominant Strategy in Game Theory

A dominated strategy is one that yields a worse payoff than another available strategy. A dominant strategy is one that yields a higher payoff than any other strategy.

Dominated Strategy in Game Theory

A dominated strategy is a strategy that is always inferior to other strategies, regardless of what the other players are doing. Because a dominated strategy consistently produces lower payoffs, rational players have no incentive to choose it. In fact, part of strategic reasoning in game theory involves identifying and eliminating dominated strategies to narrow down the set of rational and viable choices available to players.

By avoiding dominated strategies, players increase their chances of achieving better outcomes and contribute to a more predictable and efficient decision-making process for all participants in the game.

Dominant Strategy in Game Theory

A dominant strategy is a strategy that gives a player a higher payoff than anything else they could do, no matter what the other players are doing. If a player has a dominant strategy, expect them to use it.

According to game theory, each player will develop their own strategy that they believe gives them the best chance of winning, with their decisions and actions leading to different outcomes. When a player has a dominant strategy, they gain an advantage over their opponents and are in prime position to secure the best possible outcome for themselves.   

Types of Dominated Strategies in Game Theory

The two types of dominated strategies are: 

1. Strictly dominated strategy: A strategy that always delivers a worse outcome than an alternative strategy, regardless of what strategy the opponent chooses. Players will anticipate a player with a strictly dominated strategy will never play it and choose their actions accordingly. 
2. Weakly dominated strategy: A strategy that delivers an equal or worse outcome than an alternative strategy.

Types of Dominant Strategies in Game Theory

• A strictly dominant strategy will always deliver a better outcome than any other strategy, no matter what a player’s opponent does.
• A weakly dominant strategy doesn’t always deliver a better outcome, producing an equal outcome against certain strategies.

How to Eliminate Dominated Strategies and Reach a Nash Equilibrium in Game Theory

A Nash equilibrium occurs when each player chooses a strategy that is the best response to the strategies chosen by others — no player has an incentive to deviate from their strategy. 

The iterated deletion of dominated strategies is a common, though tedious, technique for simplifying games without strictly dominant strategies. In some cases, this process can reveal a Nash equilibrium; in others, it reduces the game to a smaller set of rationalizable strategies.

In the first step of this process, at most one dominated strategy is removed from the strategy space of each player, since no rational player would ever play it. This results in a new, smaller game. Some strategies that weren’t dominated before may become dominated in the reduced game.

The process is repeated until no further dominated strategies remain, assuming rationality is common knowledge among players.

There are two versions of this iterative process:

Version 1: Only Eliminate Strictly Dominated Strategies

The first (and preferred) version involves only eliminating strictly dominated strategies. If there is only one strategy for each player remaining after completing this process, that strategy set is the unique Nash equilibrium.

Version 2: Eliminate Both Strictly and Weakly Dominated Strategies

The second version involves eliminating both strictly and weakly dominated strategies. If there is a single strategy for each player at the end of the process, this strategy set is also a Nash equilibrium. Unlike the first process, eliminating weakly dominated strategies may eliminate some Nash equilibria.

As a result, the Nash equilibrium found by eliminating weakly dominated strategies may not be the only Nash equilibrium. In some games, if we remove weakly dominated strategies in a different order, we may end up with a different Nash equilibrium.

RelatedBasic Probability Theory and Statistics Terms to Know

Dominated Strategy Example

Consider the following strategic situation, which we want to represent as a game.

Two bars, Bar A and Bar B, are located near each other in the city center. Each bar seeks to maximize revenue and chooses which price to set for a beer: $2, $4 or $5. Each bar has 60 potential customers, of which 20 are locals and 40 are tourists. Locals will buy from the bar setting the lowest price (and will choose randomly if the two bars set the same price). Tourists will choose a bar randomly in any case. 

Creating a Payoff Matrix

Once we’ve identified the players and the strategies, we can begin to create our payoff matrix:

Now, we can fill in the payoffs. We’re told that each bar only cares about maximizing revenue (number of beers sold multiplied by price).

Let’s look at the strategy profile ($2, $5). That is, when Bar A charges $2 and Bar B charges $5.

In this case, all the locals will go to bar A, as will half the tourists. This gives Bar A a total of 40 beers sold at the price of $2 each, or $80 in revenue.

Bar B only manages to attract half the tourists due to its higher price. This gives Bar B a total of 20 beers sold at a price of $5 each, or $100 in revenue.

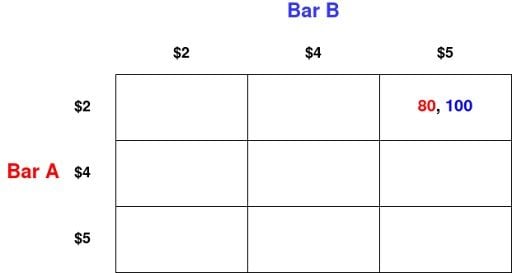
We can then fill in the rest of the table, calculating revenues in the same way.

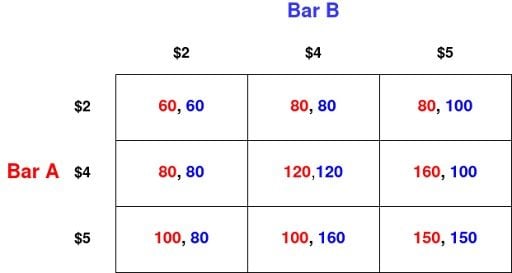
The first thing to note is that neither player has a dominant strategy. For Bar A, there is no price that will give it higher revenues than any other price it could have set, no matter what price Bar B sets.

For example, a price of $4 gives Bar A higher payoffs than any other price if Bar B prices at $5.

But what if Bar B does not price at $5 and instead prices its beer at $2? In that case, pricing at $4 is no longer Bar A’s best response. Pricing at $5 would be.

Strictly Dominated Strategy Example

The solution concept that we’ve developed so far — equilibrium dominated strategies — is not useful here.

The logic of equilibrium in dominant strategies is that if a player has a strategy that is always best, we would expect him to play it. But what if a player has a strategy that is always worse than some other strategy? It’s reasonable to expect him to never play a strategy that is always worse than another.

Player i’s strategy S is strictly dominated by another strategy S’ if, for every possible combination of strategies by all other players, S’ gives Player i higher payoffs than S.

Does either player have a strictly dominated strategy in the game above? Yes. The strategy “$2” always gives lower payoffs to Bar A than either “$4” or “$5.”

Let’s see why the strategy is strictly dominated by the strategy $4 for Bar A:

• If Bar B is expected to play $2, then Bar A earns $60 by also playing $2, but would earn $80 by switching to $4.
• If Bar B plays $4, Bar A would earn $80 with $2 pricing, but $120 with $4.
• If Bar B plays $5, Bar A would earn $80 with $2 pricing, but $160 with $4.

Therefore, Bar A would never play the strategy $2. For any possible strategy by Bar A’s opponent, there is some strategy that gives a higher payoff than the $2 strategy. We can generalize this to say that rational players never play strictly dominated strategies.

Related4 Essential Skills Every Data Scientist Needs

Iterated Deletion of Strictly Dominated Strategy Example

First Round of Deletion

So far, we’ve concluded that Bar A will never play $2, but this is a game of complete information. Bar B knows Bar A’s payoffs. So if we can spot that $2 will never be played because it is a strictly dominated strategy, Bar B can spot this, too. Bar B can thus reasonably expect that Bar A will never play $2.

This is a symmetric game, so the same holds for Bar B. Two dollars is a strictly dominated strategy for Bar B, and Bar A knows this, too. We can delete dominated strategies from the payoff matrix like so:

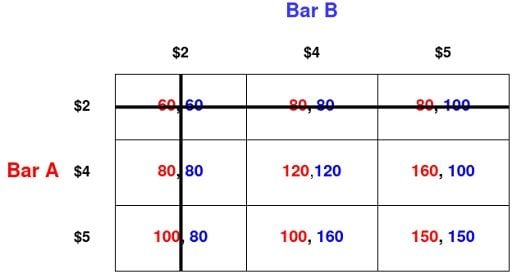
We’ve lost all cells corresponding to a strategy profile in which a dominated strategy is played. This is exactly our goal, which is to remove outcomes in which dominated strategies are played from the set of outcomes we are considering as feasible.

Second Round of Deletion

We’re now down to four strategy profiles (and four corresponding outcomes.) Let’s put ourselves in the shoes of Bar A again. Bar A knows that it will not play $2, and neither will its opponent. Bar A also knows that Bar B knows this. Now Bar A is comparing the strategies of $4 and $5 and notices that, once the strategy of $2 is taken off the table for both players, the strategy $5 is dominated by the strategy $4. That is:

• If B prices its beer at $4, matching that nets $120, and pricing at $5 nets $100.
• If B prices as $5, pricing at $4 gives $160 while matching at $5 gives $150

Pricing at $5 would only be a best response to $2, but $2 will never be played, so pricing at $5 is never a best response to any strategy a rational player would play. So, we can delete it from the matrix. The game is symmetric so the same reasoning holds for Bar B.

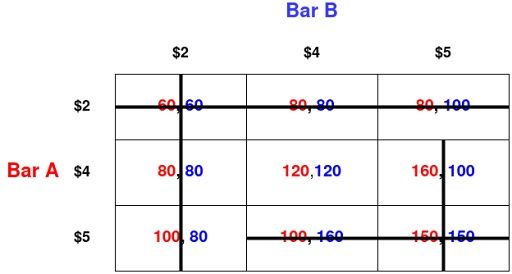
We are now down to exactly one strategy profile — both bars price their beers at $4. We used the iterated deletion of dominated strategies to arrive at this strategy profile. 

• Iterated deletion of dominated strategies: This is a method that involves first deleting any strictly dominated strategies from the original payoff matrix. Once this first step of deletion is completed, the reduced matrix is then studied and any strategies that are dominated in this new, reduced matrix are deleted. This process continues until no more strategies can be deleted.
• Rationalizable strategies: When iterated deletion of dominated strategies results in just one strategy profile, the game is said to be dominance solvable. More generally, the strategies that remain after a process of iterated deletion of strictly dominated strategies are known as rationalizable strategies
• Equilibrium in strictly dominant strategies: Whereas looking for an equilibrium in strictly dominant strategies involves finding a strategy that is always the best response for each player, looking for an equilibrium via iterated deletion involves iteratively discounting from consideration strategies that are never best responses. Notice that a dominant strategy (when one exists), by definition, strictly dominates all the others.

RelatedWhat Can We Learn From 4 Superhuman, Game-playing AIs?

Real-Life Applications of Dominated and Dominant Strategy

Classic examples of dominated and dominant strategies have been developed over the centuries, with some rooted in everyday life. Below are some of the most well-known examples that speak to the nature of human decision-making. 

Prisoner’s Dilemma

Two prisoners are interrogated individually, with the option to rat out the other or stay silent. Each prisoner reasons that it’s better to confess either way and hope the other doesn’t confess, leading to the optimal payoff. Because both prisoners reach the same conclusion, they both confess and receive harsher sentences. Both would’ve received better outcomes if they both stayed silent, but individual interest wins out in this scenario. 

Battle of the Sexes

A couple wants to spend time together over the weekend, but each wants to do a different activity. The dominant strategy is for each person to attend their preferred activity, but that defeats the purpose of spending time together. A couple could compromise by attending one person’s preferred activity one weekend and attending the other person’s preferred activity the next. This problem highlights the importance of communicating and sometimes accepting a less-than-optimal outcome to ensure the other person also receives some benefits.  

Stag Hunt 

Two hunters who are strangers to each other have the option of working together to hunt a stag — something neither can hunt on their own — or separately hunting hares, which are a smaller but more sure catch. Hunting a stag together can lead to the highest possible payoff, but hunting hares removes a lot of the risk involved in working with another hunter. This situation emphasizes how crucial trust is in getting people to work together.  

Chicken Game

The chicken game refers to two drivers driving at top speed toward each other. If one driver ‘chickens out’ and swerves first, they lose. If both drivers swerve, neither has more shame than the other, although each driver would rather be the one not to swerve and win. If neither swerves, they risk a dangerous outcome. This more extreme scenario explores the kind of risks people are ready to take and whether they’re willing to cooperate with each other.   

Matching Pennies

Players A and B each secretly place a penny heads- or tails-up on a table, revealing it after they’ve placed it. Player A wins if both pennis are heads or tails, and player B wins if the pennies don’t match. The interests of the players are in conflict since each one desires an outcome that hurts the other. However, there is a Nash equilibrium because the best strategy is to randomly place the penny on the table. In equilibrium, players randomize between heads and tails with equal probability (50 percent), making it unpredictable for the opponent.

Disadvantages of Dominated Strategy

While dominated strategies can be helpful for approaching games and real-life scenarios, there are some flaws to consider.

Ineffective When Equilibrium Isn’t Achieved

Dominated strategies have in common one major shortcoming — they do not always narrow down what may happen in a game to a tractably small number of possibilities. For example, a game has an equilibrium in dominant strategies only if all players have a dominant strategy. If this is not the case, this solution concept is not very useful.

Inapplicable to Games Where Strategies Can’t Be Eliminated

Similarly, some games may not have any strategies that can be deleted via iterated deletion. Even among games that do have some dominated strategies, the remaining set of rationalizable strategies may be very large. The predictive power may not be precise enough to be useful.

Incorrect in Some of the Assumptions Made About Players

Dominant and dominated strategies operate under the assumption that all players involved are rational. But this is often not the case. People may ignore personal interests and make decisions based on a sense of fairness or community. People are also prone to making emotional decisions and mistakes, undermining the logic of dominant and dominated strategies.

Frequently Asked Questions