Nash equilibrium is a strategy profile in game theory where no player has incentive to unilaterally deviate from their initial strategy. Each player correctly anticipates the strategy choice of all other players, and chooses their optimal strategy in response to what they anticipate everyone else will do. If the Nash equilibrium were revealed to each player individually, no player would want to switch from their initially chosen strategy, or the strategy “assigned” to them by the Nash equilibrium.
Also, no player in a Nash equilibrium has a dominant strategy, which is a strategy that is superior to others’ strategies and guarantees the best personal payoff, irregardless of other player choices.
What Is a Nash Equilibrium?
A Nash equilibrium is a strategy profile in game theory in which no player has a dominant strategy. Each player correctly anticipates the strategic choice of all other players, and thus has no incentive to unilaterally deviate from their own optimal strategy. The Nash existence theorem dictates that every finite game has at least one Nash equilibrium.
Games play a key role in artificial intelligence (AI), and game environments are a popular training mechanism in areas such as reinforcement learning or imitation learning. In theory, any multi-agent AI system can be subjected to gamified interactions between its participants.
The branch of mathematics that formulates the principles of games is game theory. Game theory enables some key capabilities required in multi-agent environments in which different AI programs interact or compete in order to accomplish a goal. The famous Nash equilibrium is the cornerstone of many AI interactions in modern systems.
To best understand this definition of the Nash equilibrium, we will look at a game in which other game theory methods like the dominated strategy equilibrium and iteratively deleting strictly dominated strategies don’t work.
Nash Equilibrium Situation Example
Two bars, Bar A and Bar B, are located near each other in the city center. Each bar seeks to maximize revenue, and chooses which price to set for a beer: $3, $4 or $5. Each bar has 60 potential customers, of which, 20 are locals and 40 are tourists. Locals will buy from the bar setting the lowest price. Tourists will choose a bar randomly.
Creating a Payoff Matrix
The only difference with respect to the first version is the strategy $2 has been switched out for the strategy $3. This is the payoff matrix of the game:
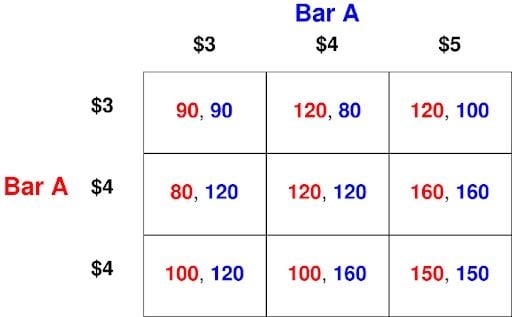
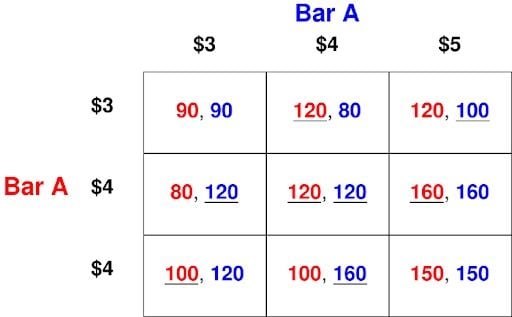
In this version of the game, neither player has dominant or dominated strategies. In other words, all three prices are rationalizable strategies for each player. Let’s see the matrix again, underlining the associated payoffs for the best responses:
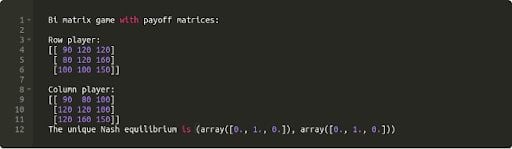
import nashpy as nash
import numpy as np
row = np.array([[90, 120, 120], [80, 120, 160], [100, 100, 150]])
column = np.array([[90, 80, 100], [120, 120, 100], [120, 160, 150]])
bars_v2 = nash.Game(row, column)
print(bars_v2)
equilibria = bars_v2.support_enumeration()
for eq in equilibria:
print(f"The unique Nash equilibrium is {eq}")
What can we say about the strategy profile for which neither payoff is underlined, such as for the strategy Profile ($3, $3)? This means that neither strategy is the best response to the other. If Bar A expected Bar B to price at $3, it would also price at $3. And the same goes for Bar B. If both players were to suspect that ($3, $3) is how the game would end up, then the game wouldn’t end up that way. Both would have incentive to deviate to a different strategy.
What can we say about a strategy profile for which only one payoff is underlined, such as for the strategy profile ($3, $4)? The player whose payoff is underlined is the best result. In this example, that is Bar A. If Bar A expected Bar B to price their beer at $4, it would be in Bar A’s best interest to price theirs at $3. There isn’t another strategy that gives a higher payoff.
But the player whose payoff is not underlined is not best responding. In this example, that is Bar B. If Bar B expects Bar A to price at $3, it should not price at $4 but rather at $5. If both players were to suspect that ($3, $4) is how the game would end up, then the game wouldn’t end up that way. One player would have incentive to deviate to a different strategy.
Finally, what can we say about a strategy profile in which all players’ payoffs are underlined? In this game, there is only one such strategy profile: ($4, $4). If both bars price at $4, each is best responding to the other. If both players were to suspect that ($4, $4) is how the game would end up, then the game would end up exactly that way. Given that Bar B is pricing at $4, pricing at $4 is Bar A’s best response. And given that Bar A is pricing at $4, pricing at $4 is Bar B’s best response.
How to Find the Nash Equilibrium
To find the Nash equilibrium, have every player in a non-cooperative game reveal their strategy to one another. If no player changes their strategy after knowing this information, then a Nash equilibrium exists.
How to Find a Nash Equilibrium
To find a Nash equilibrium, reveal the strategy of every player to one another. If no one changes their strategy after this instance, then a Nash equilibrium has occurred.
As a more in-depth example, this game below is useful in illustrating the reasoning behind the Nash equilibrium. Player 1 and Player 2 are indifferent between being alone at the neighborhood cafe or at their respective homes. However, they would like to meet and that can only happen if they both turn up at the cafe. This is the payoff matrix for this game:
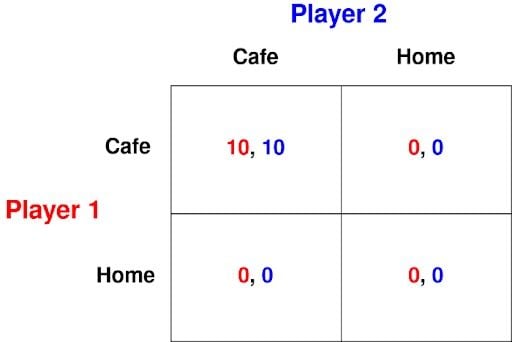
What are the Nash equilibria for this game?
import nashpy as nash
import numpy as np
row = np.array([[10, 0], [0, 0]])
column = np.array([[10, 0], [0, 0]])
meeting_game = nash.Game(row, column)
print(meeting_game)
equilibria = meeting_game.support_enumeration()
for eq in equilibria:
print(f"The unique Nash equilibrium is {eq}")
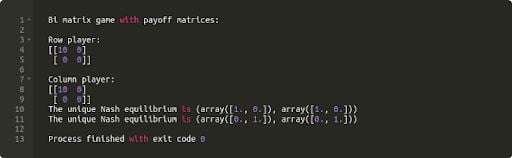
We can identify two Nash equilibria: (cafe, cafe) and (home, home).
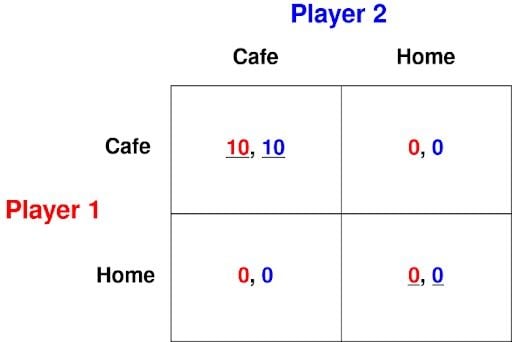
The result (home, home) may not be as convincing as (cafe, cafe) as an outcome of this game. After all, if you’re indifferent between being alone in one place or the other, and the cafe is the only place you have a remote chance of meeting the other player, why would you ever stay at home? However, (home, home) is a Nash equilibrium of this game. Next, we’ll check that it satisfies the three properties listed below. If either player were told that his counterpart was staying at home, that player may as well stay at home, too. Thus, home is a best response to home for both players, which makes (home, home) a Nash equilibrium.
How Nash Equilibrium Relates to Other Game Theory Concepts
The below image depicts the relationship of Nash equilibrium with other equilibria.
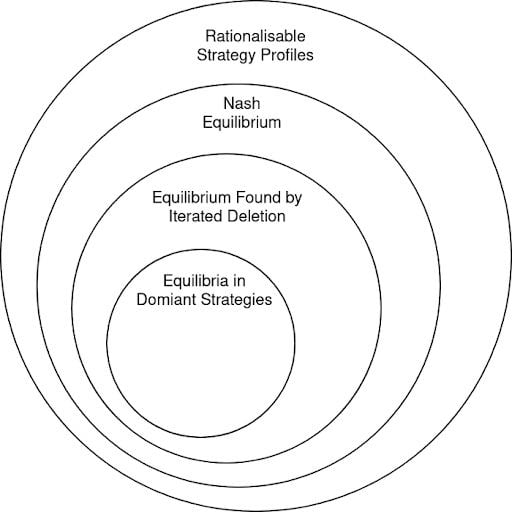
Key points to remember:
- All Nash equilibria are rationalizable strategy profiles. Iterated deletion of strictly dominated strategies will never “delete” a strategy used in a Nash equilibrium. However, not all rationalizable strategy profiles are a Nash equilibrium.
- All equilibria found by iterated deletion are Nash equilibria, but not all Nash equilibria can be found by iterated deletion (e.g. the second version of the “Two Bars Game”).
- All equilibria in dominant strategies can be found by iterated deletion (every other strategy is dominated by that one dominant strategy.) But not all equilibria found by iterated deletion are equilibria in dominant strategies.
Prisoner’s Dilemma and Nash Equilibrium
Nash equilibrium is often associated with the prisoner’s dilemma scenario in game theory. Both are concepts about player choice based on knowing other players’ strategies.
In the prisoner’s dilemma, two parties who commit a crime together are arrested. They are told separately that they will each serve one year in prison; however, each of them is offered a bargain where, if they testify against their partner, then they will go free, but the partner will have to serve three years in prison. If both parties testify against each other, then each will have to serve two years in prison. Each party cannot communicate with the other on their decision, but are both informed that they each get this bargain.
In this scenario, the Nash equilibrium presents itself if both parties take the bargain and testify against each other. This is due to each party choosing the most optimal strategy in their respective position, which would be to testify against their partner so that they would go free or at least be able to defend themselves against their partner’s choice. Though it’s worth nothing that if both parties choose this option, this leads to the least optimal outcome for all parties.
Limitations of Nash Equilibrium
While Nash equilibrium is a useful concept to apply in game theory and solution analysis, it also presents some limitations that don’t make it applicable for every game scenario.
Requires Knowing Opponent Strategies
The main limitation of the Nash equilibrium is that it requires a player to know the other players’ strategies in a competitive scenario to exist. In various competitive situations, like games, auctions or military operations, the strategies and desired outcomes of opponents are often unknown. This makes it less effective as an analysis method in real-world competition.
Doesn’t Always Lead to Optimal Outcome for All
Nash equilibrium anticipates that competing players will seek to maximize their personal payoff based on knowing others’ strategies, and make decisions accordingly. As seen in the prisoner’s dilemma scenario, both parties testifying against their partner would yield the best personal outcome, but it wouldn’t yield the best outcome for all parties (as no one testifying would). If an outcome is possible where there is an optimal payoff for all involved players, Nash equilibrium will not necessarily illustrate this possibility.
Only Occurs in Finite Games
Nash equilibrium can only occur in a finite game or a scenario where there is a finite set of player actions. This makes Nash equilibrium inapplicable toward scenarios with no defined endpoint or winners, which can encompass continuous competitions in business, historical or political contexts.
Why Nash Equilibrium Matters
The Nash equilibrium is a powerful solution concept in large part because of the following:
- Nash’s existence theorem: In all finite games (i.e., games with a finite number of players and strategies per player), there exists at least one Nash equilibrium. We will almost always be able to find at least one Nash equilibrium.
- The Nash equilibrium is computationally straightforward and elegant.
- Ability to find a large set of Nash equilibria. This is not necessarily a good thing. This solution concept still has the limitation that it may find an intractably large set of Nash equilibria.
Frequently Asked Questions
What is Nash equilibrium in game theory?
Nash equilibrium is a concept in game theory that occurs when each player in a non-cooperative game chooses and stays with their optimal strategy in response to knowing other players' anticipated strategies. Also, no player in a Nash equilibrium has a dominant strategy.
At least one Nash equilibrium exists in every finite game scenario.
How do you find Nash equilibrium?
To find Nash equilibrium, have every player in a non-cooperative game reveal their strategies to one another. If no player changes their strategy after knowing all others' strategies, a Nash equilibrium exists.





