Two’s complement is a mathematical operation on binary numbers and is how most digital systems store numbers. It’s used to signal a positive or negative integer in binary.
Two’s Complement Explained
Two’s complement is a mathematical operation on binary numbers that is used to signify positive or negative integers in binary. One method is to complement each bit and then add one, i.e. 6 in binary (0110) becomes 1010. Another method is to go right to left complementing each bit after the first 1, i.e. 10 in binary (01010) becomes 10110.
Binary numbers is a numerical system that relies on 0 and 1 to represent values that allow the computer to store and manipulate data.
How to Take the Two’s Complement
There are two common methods to take the two’s complement of a binary number. Let’s review each one:
Method One
To take the two’s complement of a number, simply complement each bit and then add one.
Example
The number 6 in binary is 0110. To take the two’s complement, complement each bit 1001, and add 1: 1010.
Method Two
Another way to take the two’s complement, is to begin with the bit on the right hand side and move towards the left until you find the first 1, Then, complement each bit after that.
Example
The number 10 in binary is 01010. The bit on the right hand side is 0, so we leave that. The next bit is 1, so each bit after that going toward the left we complement.
So, we end with 10110.
Two’s Complement and Negative Number Representation
If you take the two’s complement of a positive number, you get the negative representation of that number, and vice versa.
If you take the two’s complement of 5 (0101), you get 1011 which is how you represent -5. If you take the two’s complement of -5 (1011), you get 0101, which is 5.
How do you know if 1011 is -5, or 11?
Negative numbers are stored using two’s complement combined with what is called “signed number representation.”
With signed number representation, the most significant bit (MSB), i.e. the number on the left, is used to represent whether the number is positive (0) or negative (1). This bit is known as the “sign bit.”
You can use any number of bits to represent positive or negative numbers, as long as you follow the two’s complement method and remember that the MSB is the sign bit.
Example 1
The number 6 can be represented as 0110, so the negative representation is 1010.
We can place any number of 0’s in front of 0110, so how would you represent 6 if you used 00110? Just follow the two’s complement:00110 -> 11010.
We can see that any number of bits can be used, as long as you remember that the MSB represents the sign bit.
Example 2
To represent 6 in signed number representation, you can’t write 110. Since the MSB is 1, this number actually represents -2.
Two’s Complement Formula
With 4 bits, you can have the unsigned numbers 0 to 15 (15 = 2⁴-1). This provides us with 16 (or 2⁴) numbers in total.
Using signed number representation you can have -8 (or -2⁴–1) to +7, or (2^(4–1))–1), 16 numbers in total.
This provides us with the following formula: With n bits, we can represent signed numbers –2^(n-1) to 2^(n-1)–1. With n bits, we can represent unsigned numbers 0 to 2^(n-1).
In either case, we still have the same amount of numbers (2^n), it’s just that the signed numbers are shifted to the left half way which replaces the higher positive numbers with negative numbers.
What Numbers Can Be Represented With N Bits?
Let’s start with an example.
If you don’t care about two’s complement or signed number representation, what combinations can you have with n = 4 bits? With n = 4, you can have 2⁴ = 16 combinations, as shown in the table below:
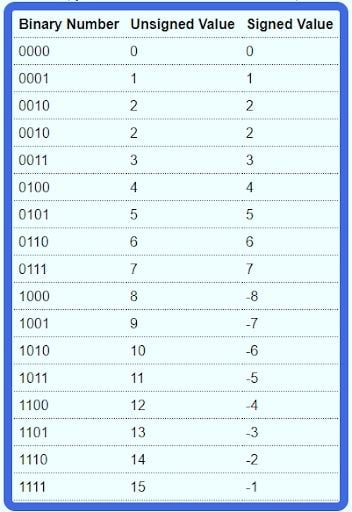
What’s the Two’s Complement of 1000?
Interestingly, if you take the two’s complement of 1000, you get 1000!
Remember 1000 is -8, and not +8, since the MSB is 1.
It’s not -0 either, since 0 and -0 are equal, and 0 is already represented by 0000. There is no need to have two representations for the one number. To represent +8, you would need an extra bit (01000).
This confuses a lot of people, however, if you just stick to the rule for taking the two’s complement, you will see that 1000 is equal to -8.
Two’s Complement: Integer Overflows in C#
If you have another look at the table above, notice how as you keep adding one, the numbers get higher until you reach 7. From 7, if you add one, you get an “overflow” and you go to the most negative number.
This is what happens in C# when you add one to an int (or some other data type) that is already the largest number it can be. When this happens, a System.OverflowException is thrown.
Now, you have an understanding of how integers work behind the scenes. You can now understand why, when adding 1, an int goes from 2147483647 (or 2³²–1) to -2147483648 (-2³²).
Why Does Int32.MaxValue = 2,147,483,647?
Many programmers know that the maximum value an int can store is 2,147,483,647, but very few actually know why.
Now, you know about two’s complement and signed number representation, you can understand why Int32.MaxValue = 2,147,483,647!
As the name of the struct suggests, Int32 integers are stored using 32 bits. The first bit (or the MSB), is the sign bit, and the next 31 bits represent the number.
With this in mind, have a look at how 2,147,483,647 is stored in memory using binary:0111 1111 1111 1111 1111 1111 1111 1111 (or 0x7FFFFFFF in Hex).
The spacing between each nibble (4 bits) is there for readability only. As you can see this is the maximum number you can store using 32 bit signed number representation.
If you tried to increase this number by 1, you would get a carry into the MSB, which would set the sign bit to 1 and all the other bits to 0. This number would then be -2,147,483,648.
