Base 12: An Introduction

Base 12, or the duodecimal system, is a numeral system that uses the number 12 as its base. The base 12 system uses 12 numerical digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A and B (where A represents 10 and B represents 11). In base 12, the number twelve is written as “10” (meaning 1 twelve and 1 zero), the number thirteen is written as “11” (meaning 1 twelve and 1 one) and so on.

Humans are accustomed to using number systems to help navigate our daily lives. The metric system, for example, is based on multiples of the number 10. There are millimeters, centimeters, decimeters, and meters. Each increases in size by a factor of 10. That’s why the metric system is known as a base 10 or decimal system.

However, there are other numeral systems as well, including base 12. While lesser known than base 10, the base 12 system is still used in several aspects of everyday life, including in timekeeping, measurement, money and currency systems and more.

Base 12 Notation

In the base 12 numbering system, the symbols used to represent the values of 10 and 11 are the letters A and B, the Greek letters Δ (delta) and Λ (lambda) or the Chinese characters 什 (shí) and 佰 (bǎi). According to the Dozenal Society — the premier global organization for the promotion of base 12 — the most popular letters for representing the numbers 10 and 11 are X and Ɛ (called “dek” and “el”), respectively.

This odd naming quirk is, perhaps, done with convenience in mind. As the numbers zero through nine only require a single digit, the base 12 system likewise wanted a single character to represent the numbers 10 and 11. 

That convention is also an advantage. Using single characters to represent the numbers 10 and 11 makes reading and writing numbers in base 12 easier. Seeing patterns and performing mental arithmetic when working with numbers in base 12 may also be easier.

How to Convert From Base 10 to Base 12

In base 12 notation, the number 22 is written as “1A” (meaning 1 twelve and 1 ten), the number 23 is written as “1B” (meaning 1 twelve and 1 eleven) and so on for double-digit base 10 numbers.

However, understanding how base 10 converts to base 12 can get a little trickier, especially with base 10 numbers that are three digits and beyond. For example, the number 200 in base 10 is written as “148” in base 12 — but this does not mean 1 twelve, 1 four and 1 eight. Instead, base 10 numbers at this size and above are converted to base 12 by putting together the remainder numbers from the base 10 number each time you divide it by 12. 

For instance, to convert “200” in base 10 to base 12, do the following:

200 / 12 = 16.66 
12 * 16 = 192
200 - 192 = 8

16 / 12 = 1.33 
12 * 1 = 12
16 - 12 = 4

1 / 12 = 0.08
12 * 0 = 0
1 - 0 = 1

From the last equation going up, put the remainder numbers together to get “148.” This is how “200” in base 10 converts to “148” in base 12.

Examples of Base 12 Systems

Although counting based on the number 12 might seem awkward at first, we use a variety of base 12 systems:

• Timekeeping: We have 12 hour clocks and 12 months in a years
• Measurement: There are 12 inches in a foot
• Money: There are 12 pennies or pence in a shilling
• Music: There are 12 keys (if you count both the black and white ones) in an octave
• Organizing: There are 12 items in a dozen and 12 dozen in a gross
• Astrology: There are 12 signs in both the western and Chinese zodiacs

RelatedHow to Read Binary Letters

Advantages of Base 12

The number 12 can be divided by six numbers: one, two, three, four, six, and 12. Because the number of those six divisors can be divided by three, 12 is known as a trichotomous number. The number 60 is also trichotomous as it can be divided by nine numbers: one, two, three, four, five, 12, 20, 30, and 60. By comparison, the number 10 can only be divided by only four numbers: one, two, five, and 10. As four can be wholly divided by two, 10 is known as a dichotomous number.

Mathematicians highly prefer trichotomous numbering systems because they are far easier to use when dividing. For example, it is easier to divide the number 12 and 60 and wind up with whole numbers than it is the number 10:

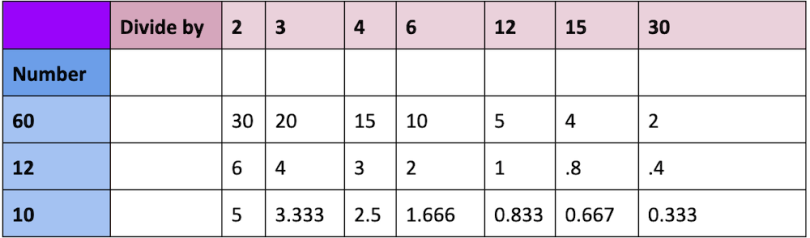
Because of this, trichotomous systems are preferable when it comes to fractions and measurements, and experts praise them as being far easier to learn:

“The duodecimal tables are easy to master, easier than the decimal ones; and in elementary teaching they would be so much more interesting, since young children would find more fascinating things to do with twelve rods or blocks than with ten. Anyone having these tables at command will do these calculations more than one-and-a-half times as fast in the duodecimal scale as in the decimal. This is my experience; I am certain that even more so it would be the experience of others.”

   — A. C. Aitken, mathematician and Fellow of the Royal Society

RelatedTwo’s Complement: A Guide

Disadvantages of Base 12

Despite base 12’s various advantages and the praise that it receives from mathematicians, its disadvantages make it less practical for widespread use in modern computing and mathematics. 

One of base 12’s  disadvantages is no fault of its own: It’s not as widely used as the standard decimal system that most modern nations use and is, therefore, not familiar to non-mathematicians. This can lead to confusion and mistakes when newer folks work with it.

The second challenge with base 12 is its limited compatibility with other systems and equipment. The decimal (or base 10) system is the global standard for most mathematical and scientific applications. As a result, many tools, such as calculators and computers, are optimized for use with base 10, not base 12. 

Then there’s the challenge of base 12’s use of special characters to represent the numbers 10 and 11 and any multiples of those numbers. Those different symbols can make them more difficult to recognize and write. Additionally, different cultures use different symbols for these two non-standard numbers, leaving no single standard that’s used or preferred. 

Translating between base 12 and other number systems is also more challenging. That’s because an additional step is required in many cases: translating base 12’s two additional characters into numbers. For example, let’s take the base 12 number 11A and convert it to base 10.

First, we’ll need to translate the symbol A to its base 10 equivalent, 10. Our new number is now 1110.

Next, we use the standard method for converting between numbering systems. We do this by taking each digit of our new number and, since we’re converting from base 12, multiplying it by a factor of 12 based on its position in the number. A brief reminder that any number to the zeroth power equals one.

So, 11A in base 12 = 168 in base 10. Simple, right?

Origins of the Base 12 System

The origins of base 12 are fascinating. Some languages in Africa and Asia have evidence of a base 12 counting system. King Charlemagne, the emperor of greater Europe during the middle ages, also used a base 12 system for his kingdom’s money. The early Egyptians drew on the power of base 12. They used sundials and sub-divided the day into 12 parts. The ancient Chinese also based their Earthly Branches concept on the number 12 because they discovered that it took roughly 12 years (11.86 to be exact) for the planet Jupiter to complete one orbit around the sun. From that discovery, the Chinese Zodiac was born.  

Of course, base 12 wasn’t the only mathematical system that our ancient forebearers used. The Mayans were known to use a base 20 system, and the Babylonians developed and used a base 60 system system. That base 60 system offers ease of divisibility, which is why we still use it today to help tell time (there are 60 seconds in a minute and 60 minutes in an hour) and for measuring angles (a circle is 360 degrees).

The Future of Base 12

Today, the use of base 10 will likely remain the global standard — and that likely won’t be changing any time soon. 

However, many opportunities still remain for understanding and using the power of base 12, as its use in measurement, music and timekeeping won’t be changing for the foreseeable future. This opportunity allows us to keep exploring base 12 and potentially get a deeper understanding of it as time goes, without needing to learn new kinds of notations or conversions.

Frequently Asked Questions