5 Probability Questions to Test Your Data Skills

As you apply for data science jobs, you’ll likely be asked a variety of probability questions during the technical aspect of the interview. Within this post, I aim to cover five different probability questions (increasing in difficulty) that I believe serve as a good representation of the different types of questions you’d expect in the interview process.

This article doesn’t intend to be the end all be all for practice, but rather aims to improve your familiarity with some of the most common probability questions.

With that said, let’s begin.

How to Solve 5 Common Probability Questions

Question 1: The Dice Roll 

Two fair dice are rolled. What is the probability that their sum is greater than four?

Answer

First, we should find the sample space. If we roll one die, each outcome (numbers one through six) all have an equal probability of 1/6. However, since we are rolling two dice, each outcome is 1/36. This means that our sample space is 36.

Now from here, there are two ways to solve the problem. We could first find the number of all the sums that are greater than four and divide by 36, or we could find the sums that are less than or equal to four and find its complement. We will be doing the latter as it will take less time to solve.

First, we find the number of ways for the outcome of our die to have a sum of four or less. This would yield in:

Also note that since the roll of each dice are independent, the order of the outcomes matter i.e. (1,2) is a different result from (2,1), and so on.

As we can see from above, we have six possible outcomes where the sum is four or less. This yields a probability of 6/36 or 1/6. Since the question asks for sums that are greater than four, we now need to find the complement of the probability we found above. Therefore, the probability of rolling two dice with their sum being greater than four is 5/6.

Interview Prep:  How to Land Your First Data Science Job

Question 2: Marble Colors

A jar contains 12 marbles: four red, five blue, and three orange. If you pull three marbles without replacement, what is the probability of getting all three colors in the order of blue, orange and red? What is the probability of getting all orange?

Answer

We first have to note “without replacement” — this means that when we pull the marble, we don’t put it back inside the jar. This means that the sample space decreases by one by each pull, starting from 12.

For the first question, we want to find the probability of marbles pulled in the order of blue, orange and red. We first need to find the probability of pulling a blue, which is 5/12.

Now, since we are not putting the marble back in the jar, we have 11 marbles remaining. The probability of pulling an orange marble is now 3/11, as opposed to 3/12.

Now in this pull, we have 10 marbles remaining. This means that the probability of pulling a red marble is 4/10. To find the probability, we now multiply the three events.

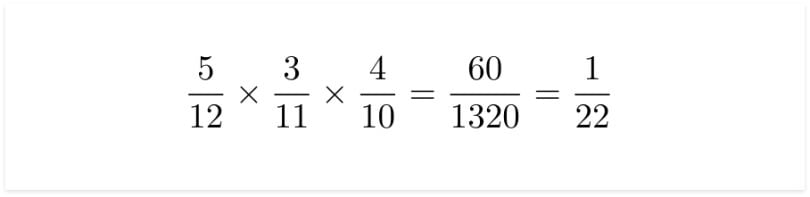
For the second question, we want to find the probability of pulling all orange marbles, also without replacement. We will follow the same procedure as above, except this time both the sample space and the number of orange marbles will both be decreasing.

For the first pull, the probability of pulling the first orange marble is 3/12. For the second pull, the probability of pulling the second orange marble is 2/11. For the last pull, the probability of pulling the third orange marble is 1/10. We multiply these outcomes and get the answer.

Interview Prep: 26 Job Interview Tips to Make a Lasting Impression

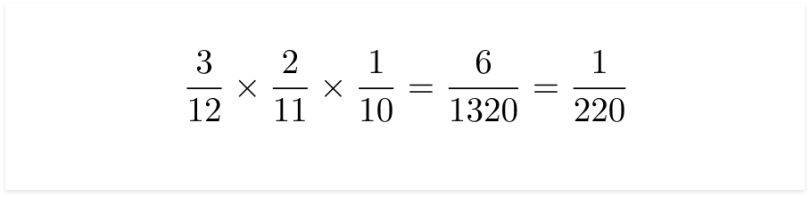
Question 3: Defective Single Board Computers

Samsung, Panasonic and LG are producing single board computers (SBCs) for hobbyists. Samsung’s SBCs take up 40 percent of the market, Panasonic’s SBCs take up 25 percent of the market and LG’s SBCs take up the rest. One percent of all Samsung and Panasonic’s SBCs are defective, whereas 2 percent of all LG SBCs are defective. If the SBC you bought was defective, what is the probability that it is an LG SBC?

Answer

Before we can begin to solve this problem, let’s write out what we know. We will use S to represent Samsung, P to represent Panasonic, L to represent LG and D to represent the defective computer.

To find the probability of an LG SBC given that the board is defective, we must use Bayes’ theorem. In the context of the problem, this means that:

Question 4: The Birthday Problem

This question is also known as the “Birthday Problem.”

In a room full of 50 people, what is the probability that at least two people have the same birthday? Assume that all birthdays are equally likely — uniform distribution — and there are 365 days in the year.

Answer

Similar to the first question, there are two ways to solve this problem, with one method being quicker than the other.

For the most efficient way to solve this question, we will first find the probability that no two people share the same birthday and find its complement. Since the question is asking if at least two people have the same birthday, its complement implies that no two people have the same birthday, which is easier to find.

Finding the probability of all 50 people having all different birthdays are as follows:

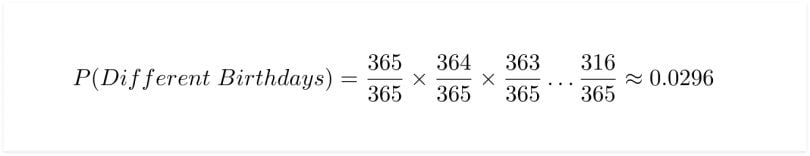
Therefore, the probability of at least two people having the same birthday is the complement of above, which is approximately 97 percent.

More on Data ScienceHow to Use the Z-Table and Create Your Own

Question 5: The Poker Hand

You are playing a game of poker, and you pull a three of a kind. This means that out of the five cards in your hand, three are the same type (Queen, Ace, 10, etc.) of different suits, and the other two are random cards from the deck. What is the probability of this hand occurring?

Answer

Before we do anything, we need to recall the binomial coefficients equation, also known as nCr. The equation is as follows:

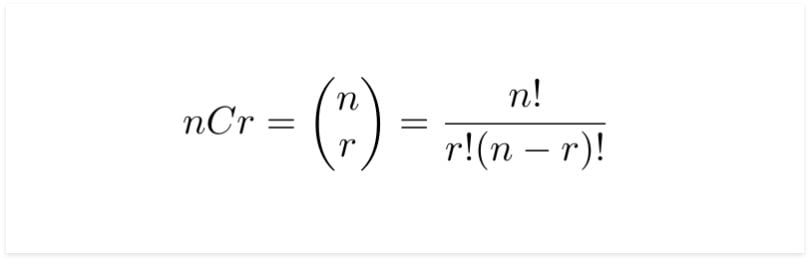
This equation is important, as it allows us to find the combinations related to our poker hand very easily. We will use definite examples as the probability will not vary from hand-to-hand, a three of a kind always results in the same probability.

Let’s assume we have three Queens, a two of hearts and a five of spades. There are 13 types of cards — Ace, 2, 3, …, King — each with four suits. 

If in our hand, we have three queens, then that is three of the four suits from 1 of the 13 types. Our other two cards will come from the other 12 types, since we must ensure we will not pull the fourth queen and the two types must be different. This means that we must choose two types from the remaining 12. Since the suit between the two other cards are independent, we will find the probability of pulling one suit out of the four and square it.

The answer is as follows:

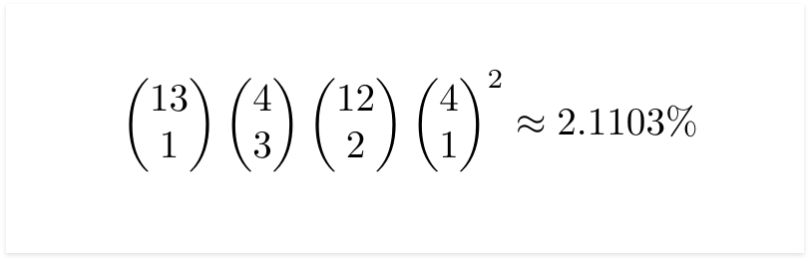
I hope these questions served as a reasonable test of your probability skills. These questions were some of my favorite ones when I began learning the basics of probability, and they’re still fun for me to solve whenever I have spare time. Best of luck on the interview process and keep excelling. 

Frequently Asked Questions