The main idea behind deep learning is that artificial intelligence should draw inspiration from the brain. This perspective gave rise to the "neural network” terminology. The brain contains billions of neurons with tens of thousands of connections between them. Deep learning algorithms resemble the brain in many conditions, as both the brain and deep learning models involve a vast number of computation units (neurons) that are not extraordinarily intelligent in isolation but become intelligent when they interact with each other.
I think people need to understand that deep learning is making a lot of things, behind-the-scenes, much better. Deep learning is already working in Google search, and in image search; it allows you to image search a term like “hug.”— Geoffrey Hinton
Neurons
The basic building block for neural networks is artificial neurons, which imitate human brain neurons. These are simple, powerful computational units that have weighted input signals and produce an output signal using an activation function. These neurons are spread across several layers in the neural network.
Below is the image of how a neuron is imitated in a neural network. The neuron takes in a input and has a particular weight with which they are connected with other neurons. Using the Activation function the nonlinearities are removed and are put into particular regions where the output is estimated.
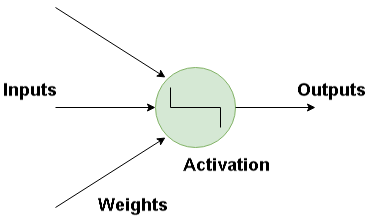
How Do Artificial Neural Network Works?
Deep learning consists of artificial neural networks that are modeled on similar networks present in the human brain. As data travels through this artificial mesh, each layer processes an aspect of the data, filters outliers, spots familiar entities, and produces the final output.
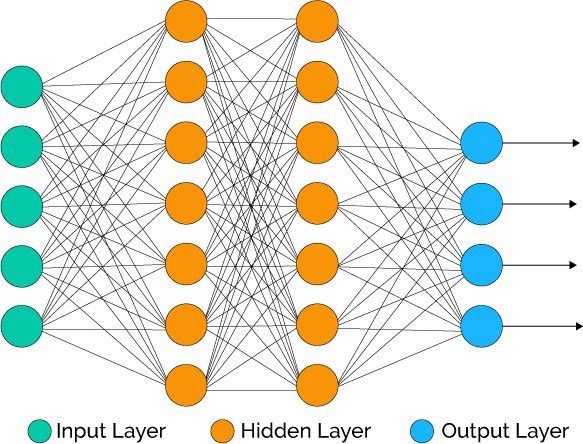
Input layer : This layer consists of the neurons that do nothing other than receiving the inputs and pass it on to the other layers. The number of layers in the input layer should be equal to the attributes or features in the dataset.
Output Layer:The output layer is the predicted feature, it basically depends on the type of model you’re building.
Hidden Layer: In between input and output layer there will be hidden layers based on the type of model. Hidden layers contain vast number of neurons. The neurons in the hidden layer apply transformations to the inputs and before passing them. As the network is trained the weights get updated, to be more predictive.
Neuron Weights
Weights refer to the strength or amplitude of a connection between two neurons, if you are familiar with linear regression you can compare weights on inputs like coefficients we use in a regression equation.Weights are often initialized to small random values, such as values in the range 0 to 1.
Feedforward Deep Networks
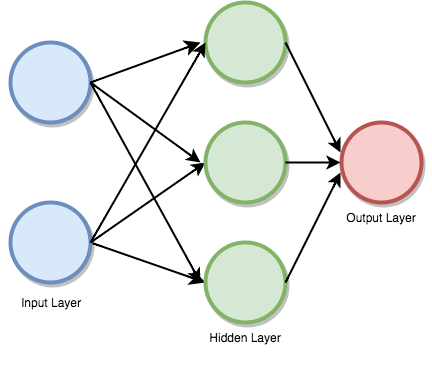
Feedforward supervised neural networks were among the first and most successful learning algorithms. They are also called deep networks, multi-layer Perceptron (MLP), or simply neural networks and the vanilla architecture with a single hidden layer is illustrated. Each Neuron is associated with another neuron with some weight,
The network processes the input upward activating neurons as it goes to finally produce an output value. This is called a forward pass on the network.
The image below depicts how data passes through the series of layers.
Activation Function
An activation function is a mapping of summed weighted input to the output of the neuron. It is called an activation/ transfer function because it governs the inception at which the neuron is activated and the strength of the output signal.
Mathematically,
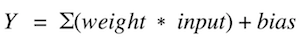
There are several activation functions that are used for different use cases. The most commonly used activation functions are relu, tanh, softmax. The cheat sheet for activation functions is given below.
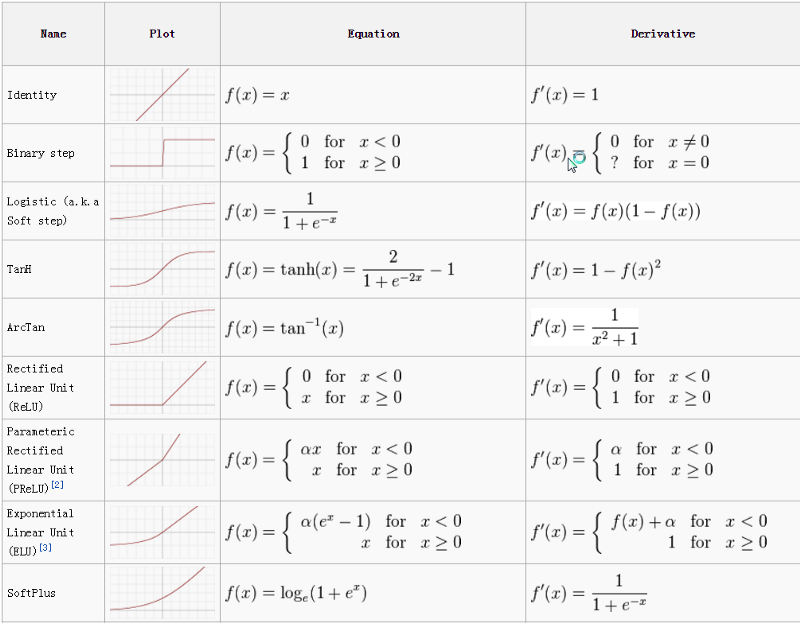
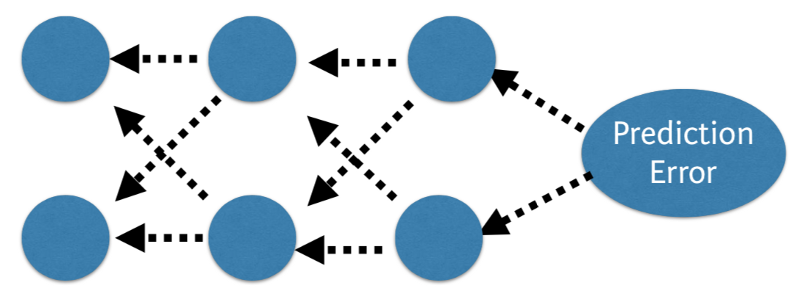
BackPropagation
The predicted value of the network is compared to the expected output, and an error is calculated using a function. This error is then propagated back within the whole network, one layer at a time, and the weights are updated according to the value that they contributed to the error. This clever bit of math is called the backpropagation algorithm. The process is repeated for all of the examples in your training data. One round of updating the network for the entire training dataset is called an epoch. A network may be trained for tens, hundreds or many thousands of epochs.
Cost Function and Gradient Descent
The cost function is the measure of “how good” a neural network did for its given training input and the expected output. It also may depend on attributes such as weights and biases.
A cost function is single-valued, not a vector because it rates how well the neural network performed as a whole. Using the gradient descent optimization algorithm, the weights are updated incrementally after each epoch.
Compatible Cost Function:
Mathematically,
Sum of squared errors (SSE)
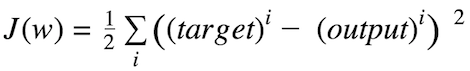
The magnitude and direction of the weight update are computed by taking a step in the opposite direction of the cost gradient.
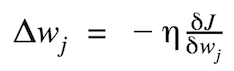
where Δw is a vector that contains the weight updates of each weight coefficient w, which are computed as follows:
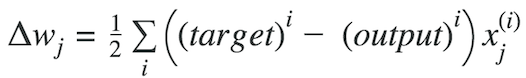
Graphically, considering cost function with single coefficient
We calculate the gradient descent until the derivative reaches the minimum error, and each step is determined by the steepness of the slope (gradient).
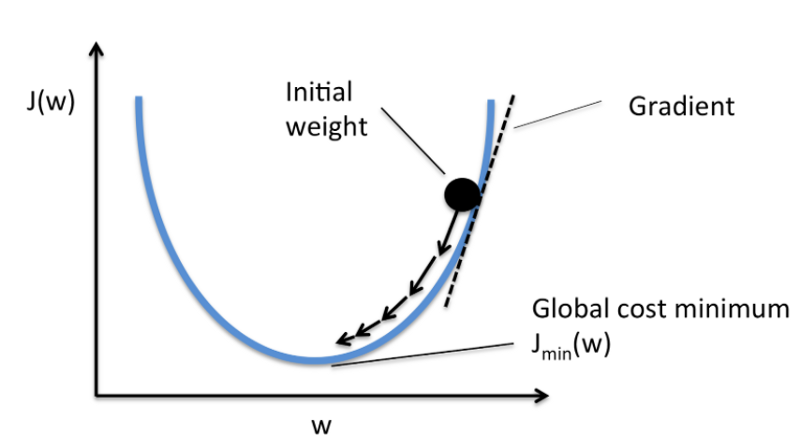
Multilayer Perceptrons (Forward Propagation)
This class of networks consists of multiple layers of neurons, usually interconnected in a feed-forward way (moving in a forward direction). Each neuron in one layer has direct connections to the neurons of the subsequent layer. In many applications, the units of these networks apply a sigmoid or relu (Rectified Linear Activation) function as an activation function.
Now consider a problem to find the number of transactions, given accounts and family members as input. To solve this first, we need to start with creating a forward propagation neural network.
Our Input layer will be the number of family members and accounts, the number of hidden layers is one, and the output layer will be the number of transactions. Given weights as shown in the figure from the input layer to the hidden layer with the number of family members 2 and number of accounts 3 as inputs. Now the values of the hidden layer (i, j) and output layer (k) will be calculated using forward propagation by the following steps.
Process
- Multiply — add process.
- Dot product (Inputs * Weights).
- Forward propagation for one data point at a time.
- Output is the prediction for that data point.
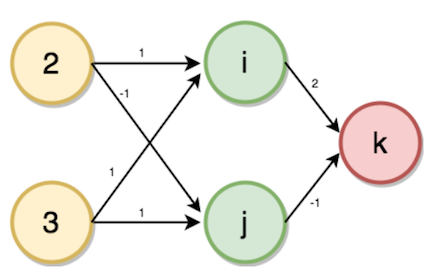
Value of i will be calculated from input value and the weights corresponding to the neuron connected.
i = (2 * 1) + (3 * 1)
→ i = 5
Similarly,
j = (2 * -1) + (3 * 1)
→ j = 1
K = (5 * 2) + (1 * -1)
→ k = 9
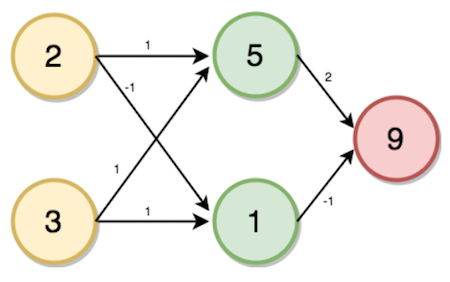
Solving the Multi Layer Perceptron problem in Python
Now that we have seen how the inputs are passed through the layers of the neural network, let’s now implement an neural network completely from scratch using a Python library called NumPy.
```
# Loading the Libraries
dl_multilayer_perceptron.py via GitHub
import numpy as np
print("Enter the two values for input layers")
print('a = ')
a = int(input())
# 2
print('b = ')
b = int(input())
# 3
input_data = np.array([a, b])
weights = {
'node_0': np.array([1, 1]),
'node_1': np.array([-1, 1]),
'output_node': np.array([2, -1])
}
node_0_value = (input_data * weights['node_0']).sum()
# 2 * 1 +3 * 1 = 5
print('node 0_hidden: {}'.format(node_0_value))
node_1_value = (input_data * weights['node_1']).sum()
# 2 * -1 + 3 * 1 = 1
print('node_1_hidden: {}'.format(node_1_value))
hidden_layer_values = np.array([node_0_value, node_1_value])
output_layer = (hidden_layer_values * weights['output_node']).sum()
print("output layer : {}".format(output_layer))
view raw$python dl_multilayer_perceptron.py
Enter the two values for input layers
a =
3
b =
4
node 0_hidden: 7
node_1_hidden: 1
output layer : 13
Using Activation Function
For neural Network to achieve their maximum predictive power we need to apply an activation function for the hidden layers.It is used to capture the non-linearities. We apply them to the input layers, hidden layers with some equation on the values.
Here we use Rectified Linear Activation (ReLU)
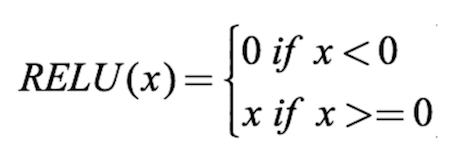
In the previous code snippet, we have seen how the output is generated using a simple feed-forward neural network, now in the code snippet below, we add an activation function where the sum of the product of inputs and weights are passed into the activation function.
dl_fp_activation.py via GitHub
import numpy as np
print("Enter the two values for input layers")
print('a = ')
a = int(input())
# 2
print('b = ')
b = int(input())
weights = {
'node_0': np.array([2, 4]),
'node_1': np.array([[4, -5]]),
'output_node': np.array([2, 7])
}
input_data = np.array([a, b])
def relu(input):
# Rectified Linear Activation
output = max(input, 0)
return(output)
node_0_input = (input_data * weights['node_0']).sum()
node_0_output = relu(node_0_input)
node_1_input = (input_data * weights['node_1']).sum()
node_1_output = relu(node_1_input)
hidden_layer_outputs = np.array([node_0_output, node_1_output])
model_output = (hidden_layer_outputs * weights['output_node']).sum()
print(model_output)$python dl_fp_activation.py
Enter the two values for input layers
a =
3
b =
4
44
Developing First Neural Network with Keras
About Keras:
Keras is a high-level neural networks API, written in Python and capable of running on top of TensorFlow, CNTK, or Theano.
It is one of the most popular frameworks for coding neural networks. Recently, Keras has been merged into tensorflow repository, boosting up more API's and allowing multiple system usage.
To install keras on your machine using PIP, run the following command.
sudo pip install kerasSteps to implement your deep learning program in Keras
- Load Data.
- Define Model.
- Compile Model.
- Fit Model.
- Evaluate Model.
- Tie It All Together.
Developing your Keras Model
Fully connected layers are described using the Dense class. The Dense class allows us to specify the number of neurons, the activation function, and the weight initializer using the kernel_initializer argument. Now that the model is defined, we can compile it. Compiling the model uses the efficient numerical libraries under the covers (the so-called backend) such as Theano or TensorFlow. So far we have defined our model and compiled it set for efficient computation. Now it is time to run the model on the PIMA data. We can train or fit our model on our data by calling the fit() function on the model.
Let’s get started with our program in KERAS: keras_pima.py via GitHub
# Importing Keras Sequential Model
from keras.models import Sequential
from keras.layers import Dense
import numpy
# Initializing the seed value to a integer.
seed = 7
numpy.random.seed(seed)
# Loading the data set (PIMA Diabetes Dataset)
dataset = numpy.loadtxt('datasets/pima-indians-diabetes.csv', delimiter=",")
# Loading the input values to X and Label values Y using slicing.
X = dataset[:, 0:8]
Y = dataset[:, 8]
# Initializing the Sequential model from KERAS.
model = Sequential()
# Creating a 16 neuron hidden layer with Linear Rectified activation function.
model.add(Dense(16, input_dim=8, kernel_initializer='uniform', activation='relu'))
# Creating a 8 neuron hidden layer.
model.add(Dense(8, kernel_initializer='uniform', activation='relu'))
# Adding a output layer.
model.add(Dense(1, init='uniform', activation='sigmoid'))
# Compiling the model
model.compile(loss='binary_crossentropy',
optimizer='adam', metrics=['accuracy'])
# Fitting the model
model.fit(X, Y, epoch=150, batch_size=10)
scores = model.evaluate(X, Y)
print("%s: %.2f%%" % (model.metrics_names[1], scores[1] * 100))$python keras_pima.py
768/768 [==============================] - 0s - loss: 0.6776 - acc: 0.6510
Epoch 2/150
768/768 [==============================] - 0s - loss: 0.6535 - acc: 0.6510
Epoch 3/150
768/768 [==============================] - 0s - loss: 0.6378 - acc: 0.6510
.
.
.
.
.
Epoch 149/150
768/768 [==============================] - 0s - loss: 0.4666 - acc: 0.7786
Epoch 150/150
768/768 [==============================] - 0s - loss: 0.4634 - acc: 0.773432/768
[>.............................] - ETA: 0sacc: 77.73%The neural network trains until 150 epochs and returns the accuracy value. The model can be used for predictions which can be achieved by the method model.
Ending Notes
Deep Learning is cutting edge technology widely used and implemented in several industries. It’s also one of the heavily researched areas in computer science. There are several neural network architectures implemented for different data types, out of these architectures, convolutional neural networks had achieved the state of the art performance in the fields of image processing techniques.
Few other architectures like Recurrent Neural Networks are applied widely for text/voice processing use cases. These neural networks, when applied to large datasets, need huge computation power and hardware acceleration, achieved by configuring Graphic Processing Units.
If you are new to using GPUs you can find free configured settings online through Kaggle Notebooks/ Google Collab Notebooks. To achieve an efficient model, one must iterate over network architecture which needs a lot of experimenting and experience. Therefore, a lot of coding practice is strongly recommended.
Frequently Asked Questions
What are the main components of a neural network?
Neural networks consist of an input layer, one or more hidden layers, an output layer and connections with weights and activation functions.
How does feedforward propagation work in a neural network?
Data moves forward through the network layer by layer. Each neuron applies weights and an activation function to generate an output, which is passed to the next layer.
What is backpropagation?
Backpropagation is the process of calculating error, propagating it backward through the network, and updating the weights to reduce future error.
What does the activation function do in a neural network?
An activation function introduces non-linearity to the network, allowing it to learn and model complex data patterns.




