Ever since childhood, we’ve been taught that 0.1 + 0.2 equals 0.3. It’s simple mathematics. However, in the baffling world of software development, things work pretty differently.
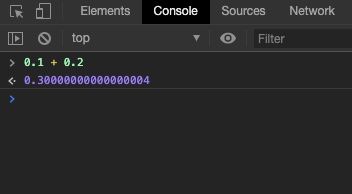
I recently started to code in JavaScript, and while reading about data types, I noticed that 0.1 + 0.2 doesn’t equal 0.3. I searched Stack Overflow for help and found a couple of posts asking similar questions.
Why 0.1 + 0.2 Doesn’t Equal 0.3 in JavaScript
In JavaScript, 0.1 +0.2 doesn’t equal 0.3 due to floating point arithmetic. JavaScript doesn’t define different types of numeric data types and always stores numbers as double precision floating point numbers, following the international IEEE 754 standard. When represented in floating point, the solution to the equation becomes 0.30000000000000004.
After doing a lot of research and math, I concluded this is not an error. It’s due to floating point arithmetic. Let’s dig deeper to understand what’s happening behind the scenes.
Why 0.1 + 0.2 Doesn’t Equal 0.3 in Most Programming Languages
Let’s look at the problem statement: How is it that 0.1 + 0.2 = 0.30000000000000004?
If you’ve programmed in languages like Java or C, you must be aware of different data types used to store values. The two data types we would be considering in the discussion ahead are integer and float.
- Integer data types store whole numbers.
- Float data types store fractional numbers.
Before we proceed, let’s understand one small concept: How are numbers represented for computational purposes? Very small and very large numbers are usually stored in scientific notation. They are represented as:
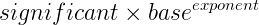
Also, a number is normalized when it is written in scientific notation, with one nonzero decimal digit before the decimal point. For example, a number 0.0005606 in scientific notation and normalized will be represented as:
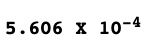
Significant is the number of significant digits that don’t include zeros, and base represents the base system used, which is decimal(10) here. Exponent represents the number of places the radix point needs to be moved left or right to be represented correctly.
How Floating Point Arithmetic Works
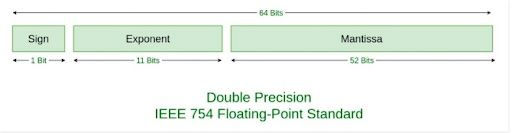
Now, there are two ways to display numbers in floating point arithmetic: single precision and double precision. Single precision uses 32 bits, and double precision uses 64 bits for floating-point arithmetic.
Unlike many other programming languages, JavaScript does not define different types of numeric data types and always stores numbers as double precision floating point numbers, following the international IEEE 754 standard.
This format stores numbers in 64 bits, where the number, the fraction), is stored in bits 0 to 51, the exponent in bits 52 to 62 and the sign in bit 63.
How to Calculate 0.1 + 0.2 in Floating Point
Let’s represent 0.1 in 64 bits following the IEEE754 standard.
The first step is converting (0.1)base 10 to its binary equivalent (base 2).
To do so, we will start by multiplying 0.1 by 2 and will separate out the digit before the decimal to get the binary equivalent.
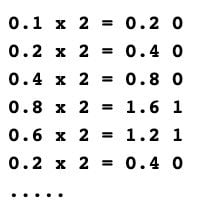
After repeating this for 64 bits, we are going to arrange them in ascending order to get our mantissa, which we are going to round off to 52 bits, as per the double precision standard.
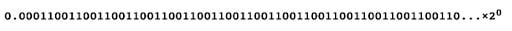
Representing it in scientific form and rounding off to the first 52 bits will yield:
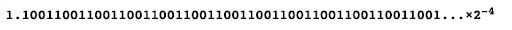
The mantissa part is ready. Now, for the exponent, we will use the calculation below:

Here, 11 represents the number of bits we are going to use for 64-bit representation of the exponent, and -4 represents the exponent from the scientific notation.
The final representation of the number 0.1 is:
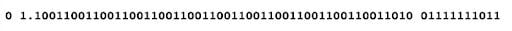
Similarly, 0.2 would be represented as:
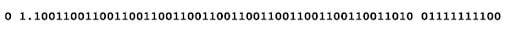
Adding the two after making the exponents same for both would give us:

When represented in floating point, this becomes:

This is represented by 0.1 + 0.2.
That is precisely the reason behind getting 0.1 + 0.2 = 0.30000000000000004.





