Would you say your pain level reading this blog post is:
- One to three: a minor annoyance, at worst
- Four to six: a real pain to get through
- Seven to 10: a public nuisance on the order of roaches or rats?
The above question and those like it — repeated ad infinitum in doctor’s offices, Gallup polls and employee exit interviews — exemplify a data type commonly referred to as “ordinal” data. (Why “ordinal,” and not “ranked” or simply “ordered,” stuck is presumably a byproduct of academics’ penchants for anachronistic language that borders on a holy mystery.)
Ordinal Data vs. Nominal Data: What’s the Difference?
- Ordinal data is data that can be ranked or ordered. Examples include data taken from a poll or survey.
- Nominal data is data that can be made to fit various categories. Examples include whether an animal is a mammal, fish, reptile, amphibian, or bird.
What Is Ordinal Data?
Ordinal data is simply what the name implies: data that is ordered or ranked. When it comes to ordinal data, however, the tricky part is a lack of consistent spacing between ranks. To flesh this out a bit more, we’ll turn to Stanley Smith Stevens and the Level of Measurement scale he pioneered.
Levels of Data Measurement
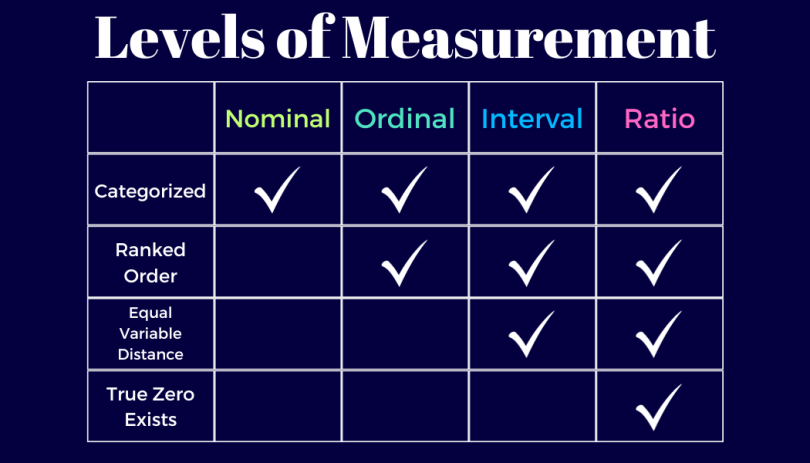
In a 1946 article in Science magazine, psychologist Stanley Stevens laid out a hierarchy of the four main types of data researchers collect — nominal, ordinal, interval and ratio. Stevens based his evaluation of each level based on its measurement precision. Here’s the differences between each level of measurement and how ordinal data fits into the scale.
Nominal Data
Nominal data is a qualitative type of data used to classify and label variables, and is known as the simplest data type on Stevens’ scale. All nominal data is categorical (meaning this data can be sorted into groups) and has no specific order or hierarchy. Variables like name, eye color and nationality are examples of nominal data.
Ordinal Data
Ordinal data is a qualitative data type that classifies variables in a ranked order. This kind of data is categorical and separates variables into groups based on distinct ascending or descending hierarchies. Ordinal data encompasses variables like educational level, economic status or level of customer satisfaction.
Interval Data
Interval data is a quantitative type of data that classifies variables in a ranked order on a scale, with equal distances (intervals) between each variable. Data in the interval level of measurement is numerical, or only in the form of numbers. Temperature in degrees, grouped income ranges and SAT scores are examples of interval data.
Ratio Data
Ratio data is a quantitative, numerical data type that is similar to interval data, except it recognizes the concept of true zero. In a ratio scale, the value of “0” cannot be measured, as “0” in a true zero sense represents nothing or the absence of a variable. This also means ratio data cannot include negative values, as there is no numerical zero to pass on the scale. Ratio data can involve measurements of height, weight or the number of members on a team.
Ordinal vs. Nominal Data
When looking at Stevens’ four levels of measurement, nominal data lies at one extreme of the scale. To collect this information, researchers simply had to classify something into a pre-defined category. Categories showed no order apart from membership based on some criteria. So, whether someone is a Democrat, Republican, or independent voter, or whether an animal is a fish, bird, mammal, reptile, amphibian, or insect are both examples of nominal data.
On the other extreme of Stevens’ scale lies ratio data, which has a true zero, equal spacing between units of observation and a scale applicable to every observation that extends from small to large. Temperature in kelvins, income, years of life, and speed are examples of ratio-scale data.
Ordinal data falls between these two extremes. Unlike its nominal cousin, ordinal categories have a rank structure. On the other hand, unlike its ratio-scale cousin, distances between ordinal ranks do not need to be equal or even standardized between rank levels.
What Is an Example of Ordinal Data?
To further illustrate the difference, consider ways of assigning ranks to students in a classroom. One teacher (presumably a tall one) wants to rank students by their heights. The scale of measurement, whether it be in inches, feet, meters, or some other, is the same for each student and equally calibrated so that measurements are directly comparable.
Another teacher (presumably a cheery one) wants to rank students by happiness. Some students surely are happier than others. But there is no standardized scale by which to measure student happiness. In lieu of a standardized, calibrated measurement, teachers must either rely on student self-reporting via a survey instrument or they must rely on external observers to judge student happiness based on some common criteria, i.e. a rubric or form. The challenge inherent in this is that the distance between one student’s being “happy” and “very happy” can be radically different from another student’s. This problem persists despite how the data are collected.
Ordinal scales beget different types of statistical inferences than do more precisely measured data. Ordinal data also makes predictive inference more challenging. But it’s not impossible. If enough ranked data can be collected in the same way, then researchers can construct empirical distributions of the frequencies of individuals’ rankings. This allows researchers to examine summary statistics like medians and interquartile ranges in ordinal-scale data. All of this flows from the natural rank structure of the ordinal scale, even though distances between ranks can differ between individuals. The simple fact that units are orderable, even though the orderings will be different from person to person, provides enough structure in the data to allow researchers to employ a range of empirical methodologies for getting at statistical regularities.
How Is Ordinal Data Used?
Because ordered data are categorized along a continuum, they can be assigned numerical likelihoods. If researchers can justifiably make distributional assumptions about these likelihoods, then they can compute probabilistic estimates of ordinal outcomes. This is especially powerful because it allows researchers to use information contained in precisely measured predictors to estimate how likely ordinal outcomes will be. To see why, let’s go back to the classroom-ranks conundrum.
If there is reason to suspect that taller people tend to be happier, student height measurements can provide a basis for probabilistic inference about how happy students are. For instance, if a student is 1.5 times taller than the class’s average height, the frequency of happiness levels reported allows teachers to claim that student is twice as likely to be “very happy” relative to other students, four times as likely to be “happy” or “very happy” relative to other students, and so on.
By exploiting the linkage between the rank-ordering of student happiness levels and student height, teachers can use movements on the height scale, which is more measurable, to decipher movements along the not-directly-measurable (or, switching back to academese, “latent”) student-happiness scale. As long as correlation exists between predictors and an ordinal outcome and researchers are willing to make assumptions (and justify them) about what distribution the ordinal outcomes likely exhibit, they can probabilistically predict ordinal outcomes.
How Is Ordinal Data Collected?
The biggest pitfall to estimating ordinal outcomes is measurement error arising from data collection. Ordinal data collection suffers more than nominal data from measurement error because nominal data are simpler to collect. Categorization of items into classes is more straightforward than both classifying and ranking items. For instance, identifying car makes as Porsche, Ford, BMW, or Subaru is easier than attempting to rank-order them based on consumer preference. Ordinal data, unlike ratio data, also suffers from imprecision due to a lack of a standardized, equally spaced continuum of measurement. Thus, direct comparison is not on offer with respect to ordinal outcomes.
For these reasons, researchers must avoid measurement error when collecting ranked outcome data. Methods for doing so include standardizing both questions on surveys and how people can respond to them. Changing categories, vague cut points, or murky wording can make for erratic, noise-filled responses.
Measurement-error likelihood also increases with second- or third-party data collection. Surveyors and respondents can both be sources of error, as can disparate observers who record totally different outcomes for the same result. Also, predictive inference and statistical estimation are complicated by the lack of a direct scale applicable across all measurements. Assumptions play a greater role in statistically examining ordinal outcomes, and unwarranted, unstated, or unrealized assumptions researchers make about data can be treacherous.
What Is Ordinal Data Used For?
Ordinal data, when well and consistently collected, allows researchers to bring statistical insight to bear on a variety of topics not broachable by more precise forms of scientific measurement. Important questions concerning overall contentment in life, subjective interpretations of job or family satisfaction, individual feelings of pain or depression, and many others can all be addressed on a large scale using ordinal outcomes. Understanding ranked information and subsequently using it to build accurate statistical models, to the extent researchers can, opens the door to a deeper understanding of subjective but common human well-being.
Frequently Asked Questions
What is the difference between ordinal data and nominal data?
Ordinal data is qualitative data that is categorized in a specific ranked order or hierarchy.
Nominal data is qualitative data that is categorized based only on descriptive characteristics. This kind of data has no ranked order or hierarchy.
What is an example of ordinal data?
Education level, economic status and level of customer satisfaction are examples of ordinal data.
