Is zero even, or odd? Or is it both? Believe it or not, there is a right answer to this question: Zero is even — and only even.
Is 0 Even?
An even number in mathematics is a number that can be written as n=2⋅k for a whole number k. If k=0, the equation 0=2⋅k remains accurate. This makes zero an even number.
To understand how we come to this conclusion, we first need to define what “even” means.
Why Is Zero Even?
An even number is a number n which can be written as n=2⋅k for a whole number k. That means if we divide an even number by two, there is no remainder left.
Can we write 0=2⋅k for some k? Yep, we can if we choose k=0.
That means that zero is even.
Is Zero Also Odd?
Again, we first need to define what “odd” means. The common definition is very similar to the definition of even.
An odd number is a number n which can be written as n=2⋅k+1 for a whole number k.
Can we write 0=2⋅k+1 for some whole number k? Nope. We can’t because solving this equation for k yields k=-1/2, which is not a whole number.
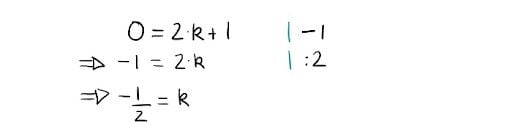
Frequently Asked Questions
Is zero an even or odd?
Zero is an even number because it is an integer and a multiple of two.
Why is zero a number?
Zero is a number because it is categorized as an integer, and integers are classified as real numbers.
Is 0 the smallest even number?
Zero is the smallest even number because it can be divided by 2, with the result still being an integer.





