The Birthday Paradox Explained

If you have a group of people in a room, how many do you need for it to be more likely than not that two or more will have the same birthday? This is the question the birthday paradox answers. 

Theoretically, the chances of two people having the same birthday are one-in-365, not accounting for leap years and the uneven distribution of birthdays across the year, and so, odds are you’ll only meet a handful of people in your life who enjoy the same birthday as you. This leads many people to intuitively guess around 180.

The correct answer, according to the birthday paradox, is just 23.

That means in each of your classes at school, amongst the fellow commuters on the bus to work and amongst the players on a soccer field, there are more than likely at least two people with the same birthday.

Humans have a notoriously poor intuition when it comes to probability. The multi-billion dollar gambling industry is proof of this.

What Is the Birthday Paradox?

The birthday paradox states  that the probability  of two people sharing the same birthday grows relative to the number of possible pairings of people, not just the group’s size. The number of pairings grows with respect to the square of the number of participants, such that a group of 23 people contains 253 unique pairs of people, or (23 x 22 / 2).

In each of these pairings, there is a 364/365 chance of having different birthdays, but this needs to happen for every pair for there to be no matching birthdays across the entire group. Therefore, the probability of two people having the same birthday in a group of 23 is:

1 — (364/365)^253 = 50.05%

If we plot the probability compared to different group sizes, we see how the probability grows as the group size increases.

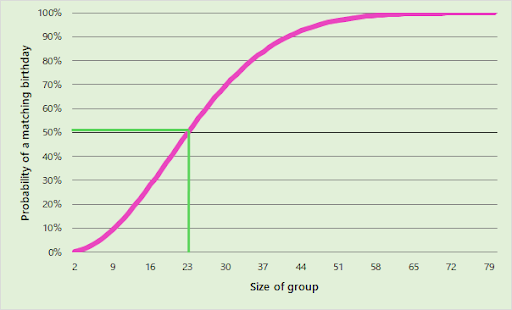
The line crosses 50 percent just before a group size of 23. Our previous guess of 180 has a probability so close to 100 percent, it’s not worth showing. In fact, the chance of choosing a group of 180 people at random, and having none of them share the same birthday, is roughly 6x10^-20, or 100 times less likely than two people picking the same grain of sand out of all the sand on Earth.

More on Statistics5 Probability Questions to Test Your Data Skills

Birthday Paradox Applications

We can generalize the birthday paradox to look at other phenomena with a similar structure.

1. Matching PINs

The probability of two people having the same PIN on their bank card is 1 in 10,000, or 0.01 percent. It would only take a group of 119 people however, to have odds in favor of two people having the same PIN.

Of course, these numbers assume a randomly sampled, uniform distribution of birthdays and PINs. In reality, birthdays peak at certain times of year and people are more likely to pick certain numbers than others for their PIN. But the lack of a uniform distribution reduces the size of the group that you need.

If we decrease the probability of a coincidence occurring, the size of the group required to get an even chance of a collision obviously increases. However, it increases much more slowly than the inverse of the probability.

For example, with a probability of 1 in 10,000, the minimum group size is 119. For a coincidence 10-times less likely, the minimum group is 373, or only 3.15 times bigger. Therefore, even for incredibly tiny probabilities, the group size doesn’t grow particularly large. For odds of one in a million, the group required is only 1,178.

2. Space junk

This has implications in the area of satellite collisions and space junk. The odds of two particular orbiting objects colliding with each other over the course of a year are almost infinitesimally small. However, given that there are around 5,500 satellites and approximately 900,000 objects of greater than 1 cm in size whizzing above our heads, collisions occur more regularly than you might expect.

Various governments are able to track the larger pieces of space junk. This allows avoidance maneuvers to take place to shift active satellites and the space station out of harm’s way. But with around 20,000 close approaches per week and growing, this could become an increasingly difficult and costly procedure.

In 2009, two satellites, a 16-year-old defunct Russian military satellite and a still active Iridium communications satellite,  collided, at a relative velocity of almost 12 km/s. Both satellites shattered into clouds of debris fragments, with over 1,000 pieces larger than a grapefruit in size.

More space junk means a higher chance of collisions occurring. And each collision increases the number of pieces of space junk. This positive feedback loop, if it exceeds the rate at which objects fall into the atmosphere and burn up, could lead to something called the Kessler Syndrome. This is a chain reaction in which collisions become increasingly common, spraying out more and more debris, until placing a satellite in low earth orbit becomes too dangerous to be feasible.

3. DNA evidence

Over the past forty years, DNA evidence has revolutionized the field of forensic investigation. As we go about our daily business, we leave behind us a trail of genetic material, mostly via skin cells and hair. Governments compile huge databases of DNA profiles, recording a series of uncorrelated genetic markers.

For some systems, the probability of two people matching on all recorded genetic markers is estimated at one in 1 trillion (excluding identical twins). Given this number is over 100 times the number of people on the planet, if a person’s DNA is found at the scene, you can be pretty sure they were there, right?

Well, not necessarily. Following the previous examples, a tiny probability can inflate into something tangible when you have a large enough group of people.

In a country the size of the US, approximately 328 million people, a match rate of one in a trillion converts to a 1 in 3,000 chance of you having a genetic profile twin, somewhere out there. In 2019, there were 16,000 murders in the US. This means there are likely around five murders a year for which the perpetrator’s DNA matches perfectly with that of another American, again, excluding identical twins. Even with the incredibly low probabilities involved, the power of the birthday paradox means that you shouldn’t convict based on DNA evidence alone, and other circumstantial evidence needs to be taken into consideration, as well.

It’s also worth considering that DNA profiling systems have improved greatly in the last thirty years. Earlier in the application of the technology, probabilities of one in a billion were often quoted. This would have given around 5,000 murders with a DNA ambiguity.

More on StatisticsThe Pigeonhole Principle Explained

4. Birthday Attack

The birthday paradox can be leveraged in a cryptographic attack on digital signatures. Digital signatures rely on something called a hash function f(x), which transforms a message or document into a very large number (hash value). This number is then combined with the signer’s secret key to create a signature. Someone reading the document could then decrypt the signature using the signer’s public key, and this would prove that the signer had digitally signed the document.

These signatures can be used to verify the authenticity of a document. By reading this article on Built In, you’re using a digital signature right now, via the HTTPS protocol. The security relies on the difficulty of finding another document with the same hash value as the signed original.

However, the birthday paradox lets us potentially abuse this system by attacking this hash function.

Let’s say Bob is an authority that digitally signs contracts. We want to trick Bob into signing a fraudulent contract, without knowing, so that we can later suggest that he approved it. What we need to find are two contracts, one legitimate and one fraudulent, which produce the same hash value when passed through f(x).

For each contract, we can identify many ways of subtly changing it, without altering its meaning. For example, you could add differing amounts of white-space at the end of each line, slightly alter the pixels in a logo or make small changes to the formatting. In combination, this gives us millions of technically different but semantically identical documents, which in Bob’s eyes would all get the stamp of approval. It also gives us millions of variations on the fraudulent document. If we find a pair of documents, one legitimate, one fraudulent, that produce the same hash, then we can pass the legitimate one to Bob for signing, and then use that signature to prove the authenticity of the fraudulent contract.

Thanks to the birthday paradox, the likelihood of at least one hash value collision between one of the legitimate and one of the fraudulent documents is much higher than might be expected, given the huge range of the hash function. In fact, the number of documents you need to produce is around the square root of the number of possible outputs of the hash function. This is improved by the fact that no hash function is perfectly uniformly distributed, which has led to many popular hashing algorithms becoming insecure.

Frequently Asked Questions