Akaike information criterion ( AIC) is a single number score that can be used to determine which of multiple models is most likely to be the best model for a given data set. It estimates models relatively, meaning that AIC scores are only useful in comparison with other AIC scores for the same data set. A lower AIC score is better.
What Is an Akaike Information Criterion (AIC) Score?
In this article, I will cover the following topics:
- What is AIC?
- When should you use AIC?
- How should the AIC results be interpreted?
- Pitfalls of AIC.
1. What is AIC?
AIC is most frequently used in situations where one is not able to easily test the model’s performance on a test set in standard machine learning practice (small data or a time series.) AIC is particularly valuable for time series, because time series analysis’ most valuable data is often the most recent, which is stuck in the validation and test sets. As a result, training on all the data and using AIC can result in improved model selection over traditional train/validation/test model selection methods.
AIC works by evaluating the model’s fit on the training data and adding a penalty term for the complexity of the model (similar fundamentals to regularization.) The desired result is to find the lowest possible AIC, which indicates the best balance of model fit with generalizability. This serves the eventual goal of maximizing fit on out-of-sample data.
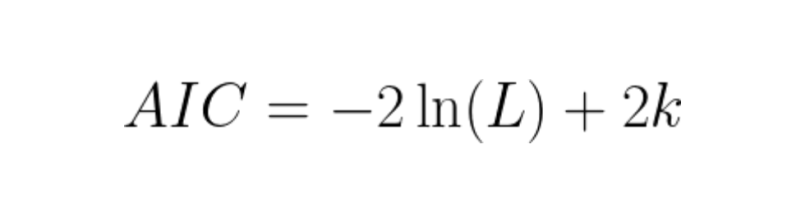
AIC uses a model’s maximum likelihood estimation (log-likelihood) as a measure of fit. Log-likelihood is a measure of how likely one is to see their observed data, given a model. The model with the maximum likelihood is the one that “fits” the data the best. The natural log of the likelihood is used as a computational convenience.
AIC is low for models with high log-likelihoods. This means the model fits the data better, which is what we want. But it adds a penalty term for models with higher parameter complexity, since more parameters means a model is more likely to overfit to the training data.
2. When Should You Use AIC?
AIC is typically used when you don’t have access to out-of-sample data and want to decide between multiple different model types, or for time convenience. My most recent motivation to use AIC was when I was quickly evaluating multiple seasonal autoregressive integrated moving average (SARIMA) models to find the best baseline model, and I wanted to quickly evaluate this while retaining all the data in my training set.
When evaluating SARIMA models, it’s important to note that AIC makes an assumption that all models are trained on the same data. So, using AIC to decide between different orders of differencing is technically invalid, since one data point is lost through each order of differencing. You must be able to fulfill AIC’s assumptions. AIC makes assumptions that you:
- Are using the same data between models.
- Are measuring the same outcome variable between models.
- Have a sample of infinite size.
That last assumption is because AIC converges to the correct answer with an infinite sample size. Often, a large sample is good enough to approximate, but since using AIC often means that you have a small sample size, there is a sample-size adjusted formula called AICc. This formula adds a correction term that converges to the AIC answer for large samples, but it gives a more accurate answer for smaller samples.
As a rule of thumb, you should always use AICc to be safe, but AICc should especially be used when the ratio of your data points (n) : # of parameters (k) is < 40.
Once the assumptions of AIC (or AICc) have been met, the biggest advantage is that your models do not need to be nested for the analysis to be valid unlike other single-number measurements of model fit like the likelihood-ratio test. A nested model is a model whose parameters are a subset of the parameters of another model. As a result, vastly different models can be compared mathematically with AIC.
3. How Should AIC Results Be Interpreted?
Once you have a set of AIC scores, what do you do with them? Pick the model with the lowest score as the best? You could do that, but AIC scores are a probabilistic ranking of the models that are likely to minimize the information loss (best fit the data). I’ll explain via the formula below.
Assume you have calculated the AICs for multiple models and you have a series of AIC scores (AIC_1, AIC_2, … AIC_n). For any given AIC_i, you can calculate the probability that the “ith” model minimizes the information loss through the formula below, where AIC_min is the lowest AIC score in your series of scores.
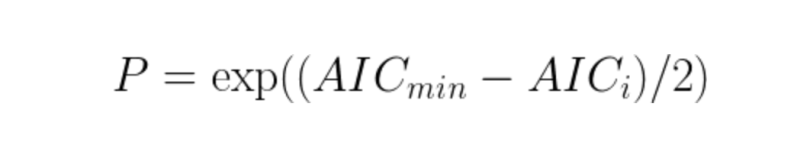
There’s a great example on this, with two sample AIC scores of 100 and 102 leading to the mathematical result that the 102-score model is 0.368 times as probable as the 100-score model to be the best model. An AIC of 110 is only 0.007 times as probable to be a better model than the 100-score AIC model. While this means that you can never know when one model is better than another from AIC — it is only using in-sample data, after all — there are strategies to handle these probabilistic results:
- Set an alpha level that, below which, competing models will be dismissed. Alpha = 0.05, for instance, would dismiss the 110-score model at 0.007.
- If you find competing models above your alpha level, you can create a weighted sum of your models in proportion to their probability. A 1:0.368, in the case of the 100 and 102-scored models.
If the precision of your answer is not of the utmost importance, and you want to simply select the lowest AIC, know that you are more likely to have picked a suboptimal model if there are other AIC scores that are close to the minimum AIC value of your experiments. A score of 100 vs 100.1 may leave you indifferent between the two models, compared to 100 versus 120, for example.
4. Pitfalls of AIC
As a reminder, AIC only measures the relative quality of models. This means that all models tested could still fit poorly. As a result, other measures are necessary to show that your model’s results are of an acceptable absolute standard (calculating the MAPE, for example.)
AIC is also a relatively simple calculation that has been built upon and surpassed by other more computationally complicated — but also typically more accurate — generalized measures. Examples of these include deviance information criterion (DIC), Watanabe-Akaike information criterion (WAIC) and leave-one-out cross-validation (LOO-CV), which AIC asymptotically approaches with large samples.
Depending on how much you care about accuracy versus computational strain, and the convenience of the calculation, given your software package’s capabilities, you may opt for AIC or one of the newer, more complicated calculations. For most calculations where one has enough data, the best (and easiest) way to accurately test your model’s performance is to use a train, validation and test set, in good machine learning practice. But if circumstances arise where that is not possible (with small data or time series analysis), AIC may be a better, go-to test of performance



