Basic Linear Algebra for Deep Learning

The concepts of linear algebra are crucial for understanding the theory behind machine learning, especially for deep learning. They give you better intuition for how algorithms really work under the hood, which enables you to make better decisions. So if you really want to be a professional in this field, you cannot escape mastering some of its concepts. This post will give you an introduction to the most important concepts of basic linear algebra that are used in machine learning.

basic linear algebra deep learning example

Table of Contents:

Introduction
Mathematical Objects
Computational Rules
Matrix Multiplication Properties
Inverse and Transpose
Summary
Resources

Introduction to Linear Algebra Basics

Linear algebra is a continuous form of mathematics and is applied throughout science and engineering because it allows you to model natural phenomena and to compute them efficiently. Because it is a form of continuous and not discrete mathematics, a lot of computer scientists don’t have a lot of experience with it. Linear algebra is also central to almost all areas of mathematics like geometry and functional analysis. Its concepts are a crucial prerequisite for understanding the theory behind machine learning, especially if you are working with deep learning algorithms.

What Is Linear Algebra?

Linear algebra is the branch of mathematics that focuses on linear equations. It is often applied to the science and engineering fields, specifically machine learning. Linear algebra is also central to almost all areas of mathematics like geometry and functional analysis.

You don’t need to understand linear algebra before getting started with machine learning, but at some point, you may want to gain a better understanding of how the different machine learning algorithms really work under the hood. This will help you to make better decisions during a machine learning system’s development. So if you really want to be a professional in this field, you will have to master the parts of linear algebra that are important for machine learning.

Video: TensorFlow

In linear algebra, data is represented by linear equations, which are presented in the form of matrices and vectors. Therefore, you are mostly dealing with matrices and vectors rather than with scalars (we will cover these terms in the following section). When you have the right libraries, like Numpy, at your disposal, you can compute complex matrix multiplication very easily with just a few lines of code. (Note: this blog post ignores concepts of linear algebra that are not important for machine learning.)

Mathematical Objects in Linear Algebra

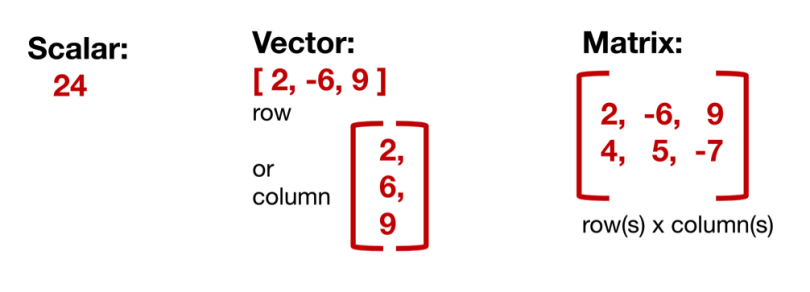
Scalar

A scalar is simply a single number. For example 24.

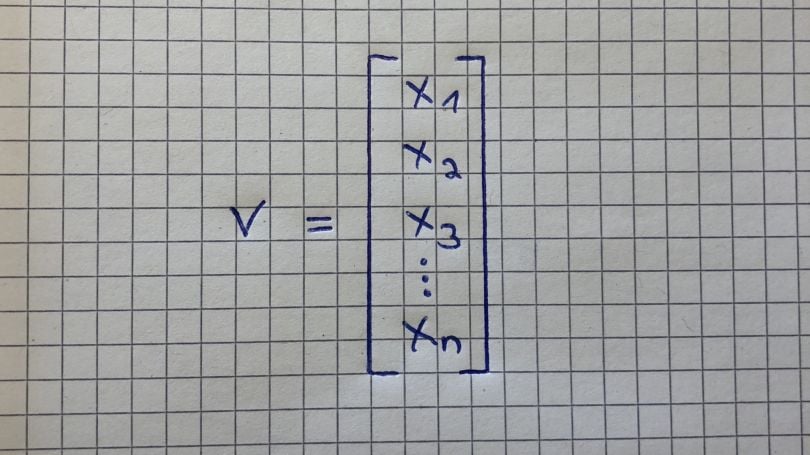
Vector

A vector is an ordered array of numbers and can be in a row or a column. A vector has just a single index, which can point to a specific value within the vector. For example, V2 refers to the second value within the vector, which is -8 in the graphic above.

Matrix

A matrix is an ordered 2D array of numbers and it has two indices. The first one points to the row and the second one to the column. For example, M23 refers to the value in the second row and the third column, which is 8 in the yellow graphic above. A matrix can have multiple numbers of rows and columns. Note that a vector is also a matrix, but with only one row or one column.

The matrix in the example in the yellow graphic is also a 2- by 3-dimensional matrix (rows x columns). Below you can see another example of a matrix along with its notation:

Tensor

You can think of a tensor as an array of numbers, arranged on a regular grid, with a variable number of axes. A tensor has three indices, where the first one points to the row, the second to the column and the third one to the axis. For example, T232 points to the second row, the third column, and the second axis. This refers to the value 0 in the right tensor in the graphic below:

tensor

Tensor is the most general term for all of these concepts above because a tensor is a multidimensional array and it can be a Vector and a Matrix, depending on the number of indices it has. For example, a first-order tensor would be a vector (1 index). A second-order tensor is a matrix (2 indices) and third-order tensors (3 indices) and higher are called higher-order tensors (3 or more indices).

Hiring NowView All Remote Data Science Jobs

Computational Rules of Linear Algebra

1. Matrix-Scalar Operations

If you multiply, divide, subtract, or add a scalar to a matrix, you do so with every element of the matrix. The image below illustrates this perfectly for multiplication:

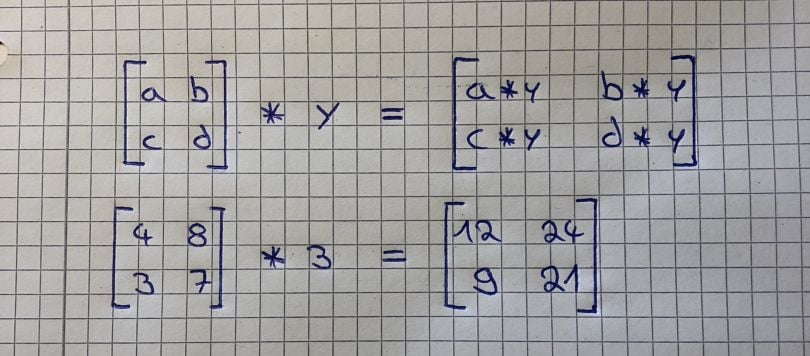
2. Matrix-Vector Multiplication

Multiplying a matrix by a vector can be thought of as multiplying each row of the matrix by the column of the vector. The output will be a vector that has the same number of rows as the matrix. The image below shows how this works:

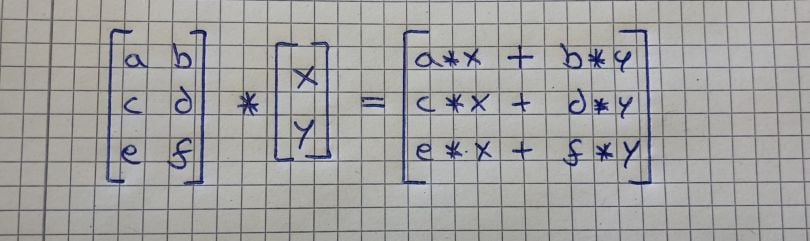
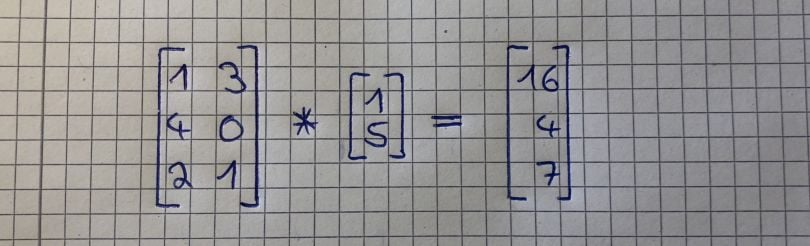
To better understand the concept, we will go through the calculation of the second image. To get the first value of the resulting vector (16), we take the numbers of the vector we want to multiply with the matrix (1 and 5), and multiply them with the numbers of the first row of the matrix (1 and 3). This looks like this:

1*1 + 3*5 = 16

We do the same for the values within the second row of the matrix:

4*1 + 0*5 = 4

And again for the third row of the matrix:

2*1 + 1*5 = 7

Here is another example:

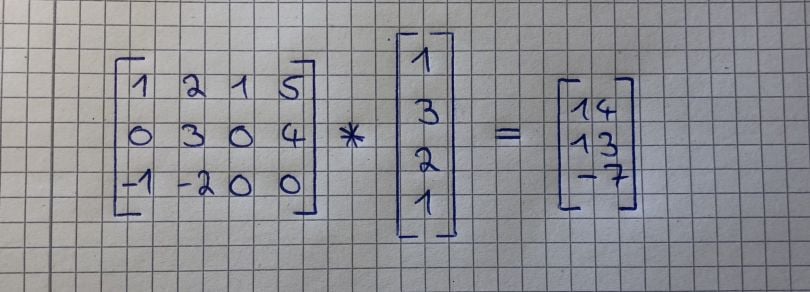
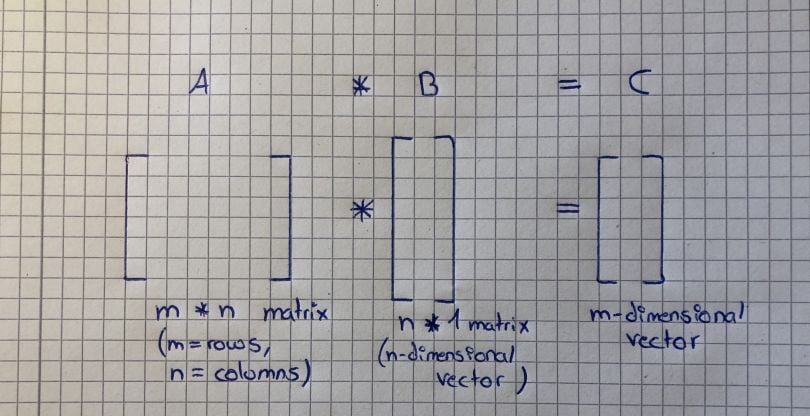
And here is a kind of cheat sheet:

3. Matrix-Matrix Addition and Subtraction

Matrix-matrix addition and subtraction is fairly easy and straightforward. The requirement is that the matrices have the same dimensions and the result is a matrix that has also the same dimensions. You just add or subtract each value of the first matrix with its corresponding value in the second matrix. See below:

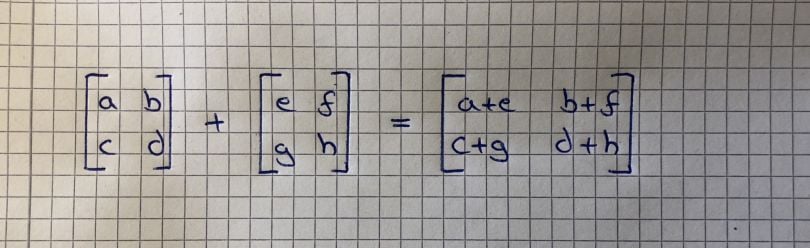
4. Matrix-Matrix Multiplication

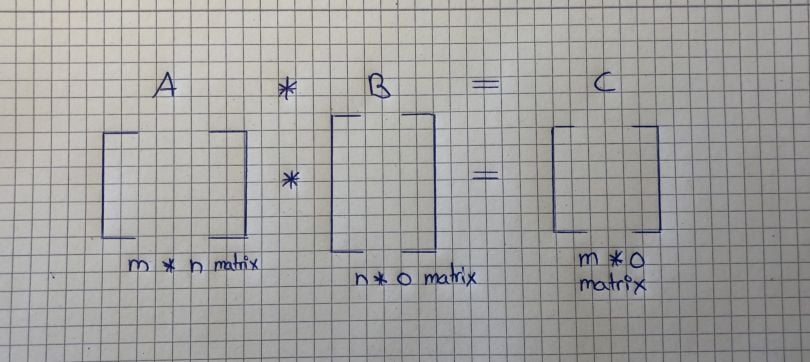
Multiplying two matrices together isn’t that hard either if you know how to multiply a matrix by a vector. Note that you can only multiply matrices together if the number of the first matrix’s columns matches the number of the second matrix’s rows. The result will be a matrix with the same number of rows as the first matrix and the same number of columns as the second matrix. It works as follows:

You simply split the second matrix into column-vectors and multiply the first matrix separately by each of these vectors. Then you put the results in a new matrix (without adding them up!). The image below explains this step by step:

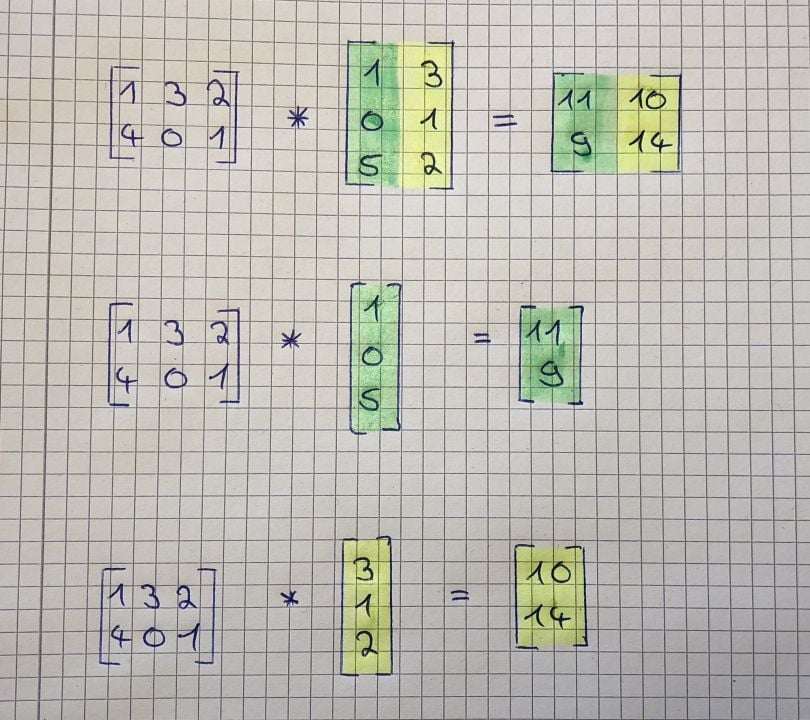
And here is again some kind of cheat sheet:

Matrix Multiplication Properties

Matrix multiplication has several properties that allow us to bundle a lot of computation into one matrix multiplication. We will discuss them one by one below. We will start by explaining these concepts with Scalars and then with matrices because this will give you a better understanding of the process.

1. Not Commutative

Scalar multiplication is commutative but matrix multiplication is not. This means that when we are multiplying scalars, 7*3 is the same as 3*7. But when we multiply matrices by each other, A*B isn’t the same as B*A.

2. Associative

Scalar and matrix multiplication are both associative. This means that the scalar multiplication 3(5*3) is the same as (3*5)3 and that the matrix multiplication A(B*C) is the same as (A*B)C.

3. Distributive

Scalar and matrix multiplication are also both distributive. This means that
3(5 + 3) is the same as 3*5 + 3*3 and that A(B+C) is the same as A*B + A*C.

4. Identity Matrix

The identity matrix is a special kind of matrix but first, we need to define what an Identity is. The number 1 is an identity because everything you multiply with 1 is equal to itself. Therefore every matrix that is multiplied by an identity matrix is equal to itself. For example, matrix A times its identity-matrix is equal to A.

You can spot an identity matrix by the fact that it has ones along its diagonals and that every other value is zero. It is also a “squared matrix,” meaning that its number of rows matches its number of columns.

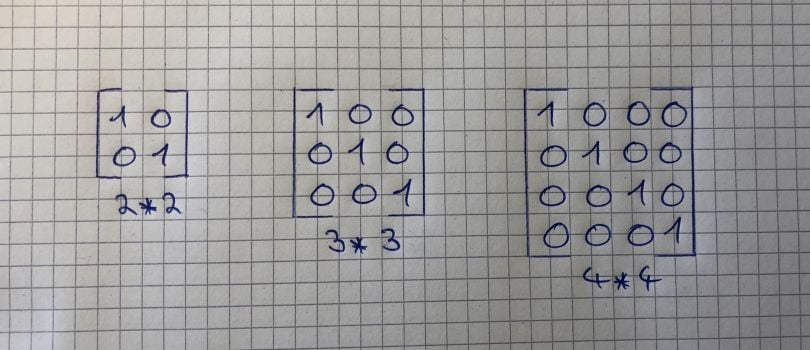
We previously discussed that matrix multiplication is not commutative but there is one exception, namely if we multiply a matrix by an identity matrix. Therefore, the following equation is true: A*I = I*A = A

Inverse and Transpose

The matrix inverse and the matrix transpose are two special kinds of matrix properties. Again, we will start by discussing how these properties relate to real numbers and then how they relate to matrices.

1. Inverse

First of all, what is an inverse? A number that is multiplied by its inverse is equal to 1. Note that every number except 0 has an inverse. If you multiply a matrix by its inverse, the result is its identity matrix. The example below shows what the inverse of scalars looks like:

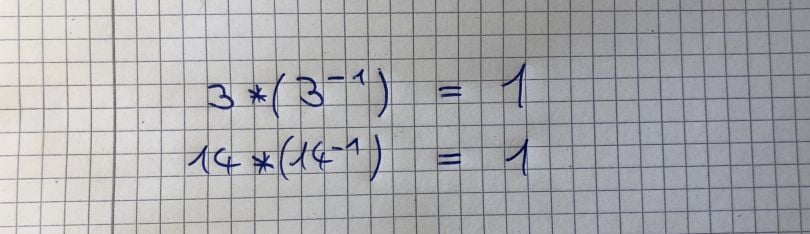
But not every matrix has an inverse. You can compute the inverse of a Matrix if it is a “squared matrix” and if it has an inverse. Discussing which matrices have an inverse would be unfortunately out of the scope of this post.

Why do we need an inverse? Because we can’t divide matrices. There is no concept of dividing by a matrix but we can multiply a matrix by an inverse, which results essentially in the same thing.

The image below shows a matrix multiplied by its inverse, which results in a 2-by-2 identity matrix.

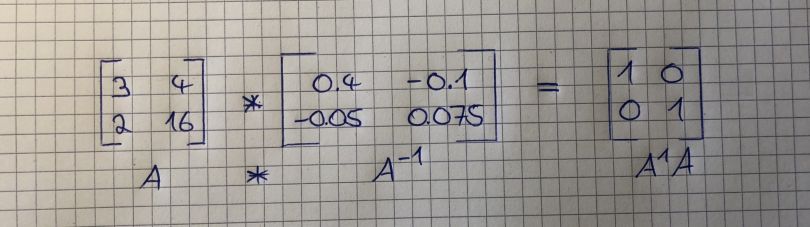
You can easily compute the inverse of a matrix (if it has one) using Numpy. Here is the link to the documentation: https://docs.scipy.org/doc/numpy-1.14.0/reference/generated/numpy.linalg.inv.html.

2. Transpose

And lastly, we will discuss the matrix transpose property. This is basically the mirror image of a matrix, along a 45-degree axis. It is fairly simple to get the transpose of a matrix. Its first column is the first row of the matrix transpose and the second column is the second row of the matrix transpose. An m*n matrix is transformed into an n*m matrix. Also, the Aij element of A is equal to the Aji(transpose) element. The image below illustrates that:

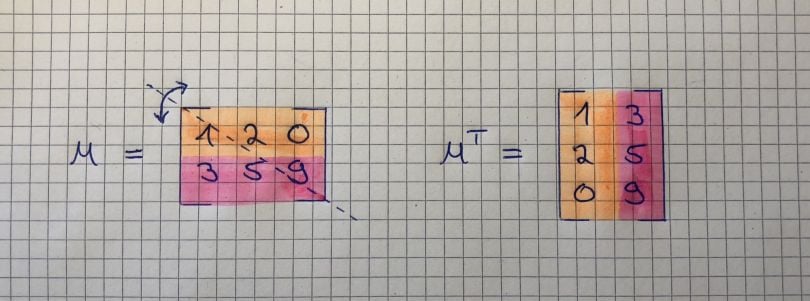
Summary of Linear Algebra Basics

In this post, you learned about the mathematical objects of linear algebra that are used in machine learning. You learned how to multiply, divide, add and subtract these mathematical objects. Furthermore, you have learned about the most important properties of matrices and why they enable us to make more efficient computations. On top of that, you have learned what inverse and transpose matrices are and what you can do with them. Although there are also other parts of linear algebra used in machine learning, this post gave you a proper introduction to the most important concepts.