What Is Exploratory Spatial Data Analysis (ESDA)?

What do you do when you want to explore patterns from data based on location? How do you know that your location data isn’t random? Is it enough to rely on correlation? Or are there any other statistical methods used for this kind of exploratory data analysis?

In this tutorial, I’ll show you how you can perform exploratory data analysis for your location data with simple and easy steps using Python. The code is also available for this tutorial in GitHub.

Exploratory Spatial Data Analysis

In data science, we tend to explore and investigate data before doing any modeling or processing a task. This helps you identify patterns, summarize the main characteristics of the data or test a hypothesis. The conventional exploratory data analysis does not investigate the location component of the data set explicitly but instead deals with the relationship between variables and how they affect each other. In other words, statistical methods dealing with correlation are often used to explore the relationship between variables.

In contrast, exploratory spatial data analysis (ESDA) correlates a specific variable to a location, taking into account the values of the same variable in the neighborhood. The methods used for this purpose are called spatial autocorrelation.

Spatial autocorrelation describes the presence (or absence) of spatial variations in a given variable. Like conventional correlation methods, spatial autocorrelation has positive and negative values. Positive spatial autocorrelation is when areas close to each other have similar values (high-high or low-low). On the other hand, negative spatial autocorrelation indicates that neighborhood areas are different (low values next to high values).

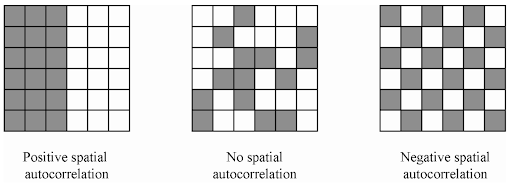
There are mainly two methods of ESDA: global and local spatial autocorrelation. The global spatial autocorrelation focuses on the overall trend in the data set and tells us the degree of clustering in the data set. In contrast, The local spatial autocorrelation detects variability and divergence in the data set, which helps us identify hot and cold spots in the data.

More From Abdishakur HassanThe 7 Best Thematic Map Types for Geospatial Data

Getting the Data

In this tutorial, we’ll use the Airbnb data set (point data set) and the layer super output areas  — LSOA  —  neighborhoods in London (polygon data set). We’ve prepared the data using spatial join to connect each point of Airbnb listings to neighborhood areas. 

If you’d like to understand and use the powerful spatial join tool in your workflow, I have a tutorial on that, too. 

The clean data set we’re using is spatially joined London Airbnb properties with an average price of properties in each local area (neighborhood). 

For this tutorial, we’ll use Pandas, Geopandas and Python Spatial Analysis Library (PySAL) libraries. So first things first: let’s import these libraries.

import pandas as pd
import geopandas as gpd
import matplotlib.pyplot as plt
import pysal
from pysal import esda, weights
from esda.moran import Moran, Moran_Local
import splot
from splot.esda import moran_scatterplot, plot_moran, lisa_cluster
We can read the data in Geopandas.
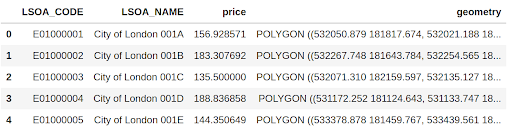
avrg_price_airbnb = gpd.read_file("london-airbnb-avrgprice.shp")
avrg_price_airbnb.head()

Since we have a geometry column (latitude and longitude), we can map the data. Here’s a choropleth map of the average prices per neighborhood.

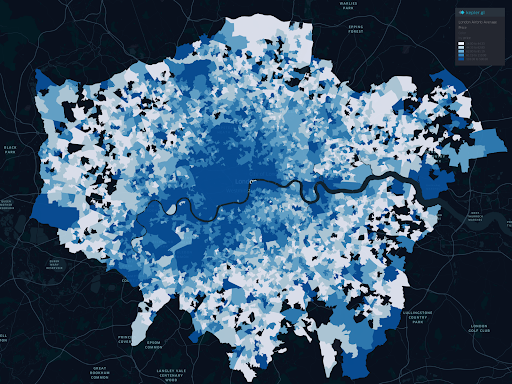
Well, with this choropleth map, we can see binned price ranges, but that doesn’t give us any statistics to determine if there is spatial autocorrelation (positive, negative or even where the hot and coldspots are). We’ll do that next.

Spatial Weights and Spatial Lag

Before we perform any spatial autocorrelation, we first need to determine the spatial weights and spatial lag.

Spatial weights are how we determine the area’s neighborhood. There are different statistical methods we use to determine spatial weights but one of the most commonly used spatial weight methods is the queen contiguity matrix. Here’s a diagram explaining how it works (alongside the rook contiguity matrix for good measure).

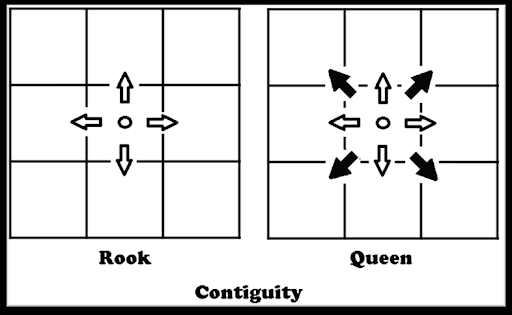
To calculate queen contiguity spatial weights, we use PySAL.

w = weights.Queen.from_dataframe(avrg_price_airbnb, idVariable="LSOA_CODE" )
w.transform = "R"

avrg_price_airbnb["w_price"] = weights.lag_spatial(w, avrg_price_airbnb["price"])

Global Spatial Autocorrelation

Global spatial autocorrelation determines the overall pattern in the data set. Here we can calculate if there is a trend and summarize the variable of interest. We typically use Moran’s I statistics to determine the global spatial autocorrelation, so let’s calculate that.

y = avrg_price_airbnb["price"]
moran = Moran(y, w)
moran.I

Remember we’re determining only the global autocorrelation with Moran’s I statistics. This calculation doesn’t tell us where this positive spatial autocorrelation exists. (Don’t worry,  that next.)

We use Moran’s I plot to visualize the global spatial autocorrelation, which is identical to other scatter plots, with a linear fit that shows the relationship between the two variables.

fig, ax = moran_scatterplot(moran, aspect_equal=True)

plt.show()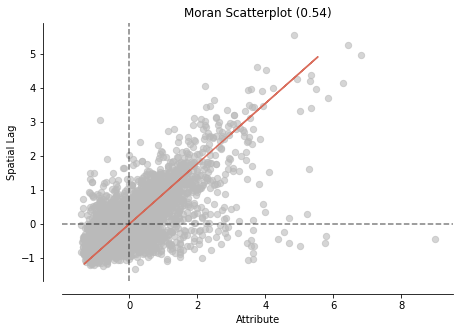

Both Moran’s I and Moran’s I scatter plot show positively correlated observations by location in the data set. Let’s see where we have spatial variations in the data set.

Get Professional Advice From Built In’s Data Science Experts4 Types of Projects You Need in Your Data Science Portfolio

Local Spatial Autocorrelation

So far, we’ve only determined that there is a positive spatial autocorrelation between the price of properties in neighborhoods and their locations. We have not yet detected where clusters are. Local indicators of spatial association (LISA) are used to do that. LISA classifies areas into four groups: high values near to high values (HH), low values with nearby low values (LL), low values with high values in its neighborhood and vice-versa.

We’ve already calculated the weights (w) and determined the price as our variable of interest(y). To calculate Moran local, we use PySAL’s functionality.

# calculate Moran Local
m_local = Moran_Local(y, w)

# Plot
fig, ax = moran_scatterplot(m_local, p=0.05)
ax.set_xlabel('Price')
ax.set_ylabel('Spatial Lag of Price')
plt.text(1.95, 0.5, "HH", fontsize=25)
plt.text(1.95, -1.5, "HL", fontsize=25)
plt.text(-2, 1, "LH", fontsize=25)
plt.text(-1, -1, "LL", fontsize=25)
plt.show()

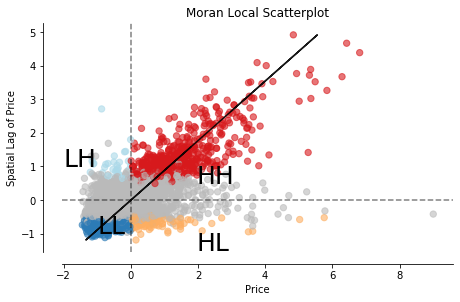
Now this is cool. We can see all values classified into four groups, but the exciting part is to see where these values cluster together in a map. Again, there is a function in PySAL (splot) to plot a map of the LISA results.

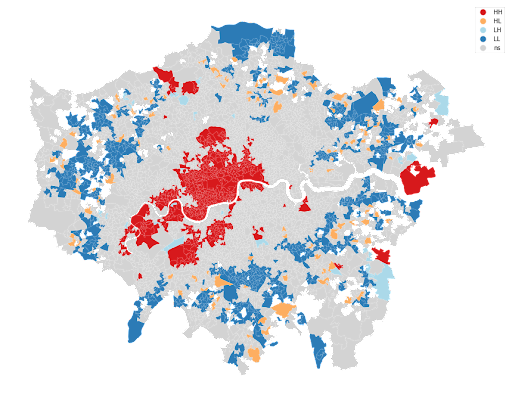
The map above shows the variation in the average price of Airbnb properties. The red colors indicate neighborhoods clustered together, which have high prices surrounded by high prices as well (mostly the center of the city). The blue areas indicate where prices are low, also surrounded by areas with low-value prices (mostly peripheries). Equally interesting is the low-high and high-low area concentration.

Compared to the choropleth map we started with this tutorial, the LISA is less cluttered and provides a clear picture of the data set. ESDA techniques are powerful tools that help you identify spatial autocorrelation and local clusters that you can apply to any given variable.