Do you recall who lost the 1936 presidential election? Kudos for knowing the also-ran. Alf Landon was an American political figure who is now virtually hidden to posterity. Landon, then the Republican governor of Kansas, campaigned for president against the incumbent, Franklin Delano Roosevelt, and heartily lost. The real figure to emerge from the election, though, was not the already famous FDR, nor was it the now-obscure Landon, but a then-unknown data collection method known as representative sampling and one of its most famous proponents.
Leading up to the 1936 election, the Literary Digest magazine, as it had for 20 years, conducted a straw poll to gauge Americans’ voting preferences. The Digest, using its polled samples, had at that point correctly called every presidential election since 1916. In August of 1936, the magazine revealed the breathtaking size of its presidential poll. The Digest announced it would sample ¼ of the country’s voting population. Ten million voters’ preferences were to be collected, processed, and distilled to “know to within a fraction of 1 percent the actual popular vote of 40 million [voters].”
When the Digest concluded its polling, 2.4 million Americans’ ballot preferences predicted a dominant 57 percent to 43 percent victory for Alf Landon. Countering this claim was then-unknown pollster George Gallup. He used a sample of only 50,000 Americans to accurately predict a landslide victory for Roosevelt. Not only did Gallup call the election correctly, but he also replicated the Digest’s polling strategy and correctly predicted its losing margin to within 1.1 percent. How did he do it?
The same article in which the Digest listed its poll’s impressive sample size also detailed its sampling strategy. The idea was to survey individuals culled from listed telephone numbers, automobile registries, country club membership rolls, and magazine subscriber lists. In 1936, during the Great Depression, telephones, cars, and magazines were expensive luxuries. Many of the surveyees owning these products had incomes that skewed much higher than the typical American voter. These wealthier individuals were also more likely to vote Republican.
The Digest poll also suffered from non-response bias: only a quarter of the 10 million people surveyed actually responded. Those that did were more likely to come out against Roosevelt. Gallup’s poll, on the other hand, dispatched data collectors to interview Americans chosen at random from a representative cross-section of U.S. demographics and income ranges. Gallup’s recreation of the Digest’s polling strategy was exact, however. He sampled similar telephone, country club, and car registry listings and came up with estimates closely resembling those of the Digest’s survey using a sample of only 3,000 individuals. In so doing, Gallup was able to recreate the Digest’s oversampling of likely Landon voters and recreate the magazine’s erroneous results prior to the presidential election.
This historical example illustrates a central problem of data analytics: More data does not necessarily provide better insights. If the sampling strategy is ill-considered, data measurement can be erroneous and can mislead researchers. Reliance on a poorly conceived data-collection process to provide large-sample inference cuts down on idiosyncratic statistical noise and, insidiously, can impart more confidence to misleading conclusions. One of the “Five Myths of Measurement Error” is that measurement error can be alleviated by collecting larger numbers of observations. The authors suggest that, in the presence of measurement error, even huge amounts of badly collected data can be outperformed by small amounts of data sampled without systemic error.
Nor is there reason to believe that statistical relationships between measured variables and an outcome of interest are simply attenuated by measurement error. The bias can go in either direction. The source of the error in data collection and how it affects not only impacts of measured variables on an outcome, but also relationships between measured variables, can result in either over- or under-inflated statistical estimates. It’s simply false that if results are measured with error, then these results would be stronger without error. Essentially, the problem is that the sampling strategy results in a correlation between measured variables and the sampling strategy which can, itself, be thought of as an unmeasured variable typically represented by a statistical error term. In this sense, erroneous measurement resulting from a flawed sampling design resembles omitted variables bias. What’s more, measurement error is frequently either glossed over or ignored when researchers report findings.
To illustrate, here’s a thought experiment: Public-health officials want to measure the prevalence of a disease circulating in a population. Assume that the true probability of infection is 0.35 in a population of a million people. Public-health authorities employ one of two strategies to sample 5,000 potential infectees. The first strategy is to randomly sample and test individuals from the population. The second strategy is to only sample and test those individuals who exhibit symptoms of the disease. Further, assume that 50 percent of infectees are symptomatic and that tests for the disease have high accuracy. The second strategy has many potential sources of measurement error: symptoms of the disease can be indicative of other diseases to a greater or lesser extent; symptomatic patients may have a more virulent form of the disease that’s easier to detect than non-symptomatic patients; and symptomatic individuals can, themselves, select to get tested or not. These and other reasons could result in an unmeasured correlation between the estimated prevalence of disease spread and the data collection strategy. For illustrative purposes, pretend this correlation between the data collection procedure and the collected data is positive and lies in the range from 0 to 0.7.
The figure below represents what happens as more data is collected under both strategies (code available here):
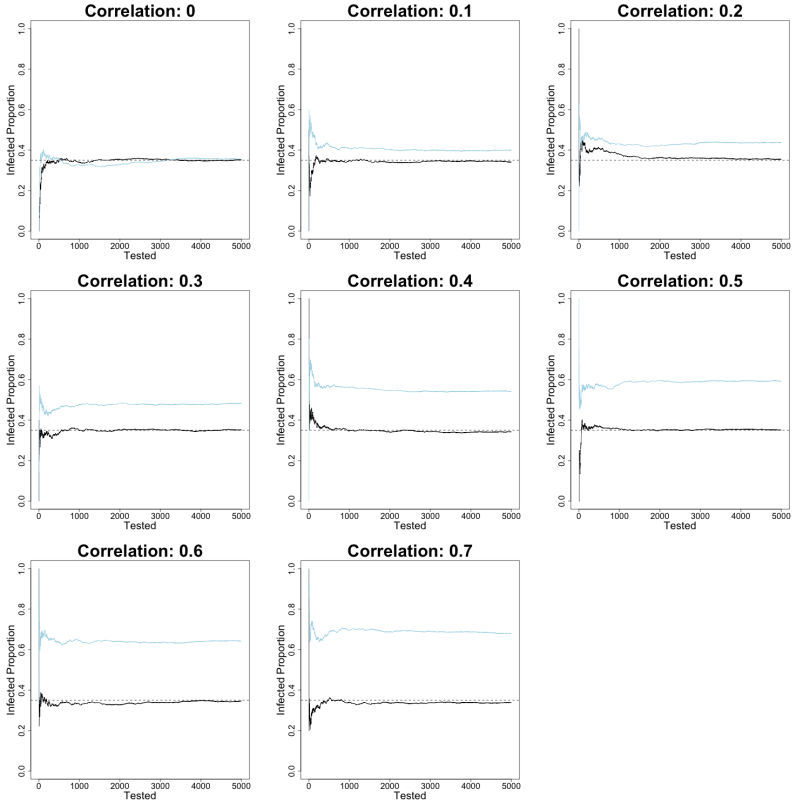
The dotted line at 0.35 of the Infected Proportion axis represents the population disease prevalence. The solid black line charts data collected from the strategy of randomly sampling and testing 5,000 individuals from the million-person population. The light-blue line represents data collected only from tests of symptomatic individuals. As the number of individuals tested for the disease (the Tested axis) increases past the first few hundred, the black random-sampling line settles on to the dashed population prevalence in all cases. When the assumed correlation between sampling symptomatic individuals and the sampling procedure is 0, the light-blue line exhibits this same behavior. Idiosyncratic errors of the data collection process cancel out as more individuals are tested regardless of symptoms. Both strategies eventually yield a close estimate of the population prevalence.
As the correlation between having symptoms and being tested increases, however, the light-blue line settles into a relatively higher estimate of disease prevalence than the black line. This expanding difference between the two lines across assumed correlations is the result of data that increasingly measures how likely a person is to be tested and to test positive for the disease given that they have symptoms. Thus, as the correlation between being tested and displaying disease symptoms increases, so does the estimate of the proportion of symptomatic disease in the population. This is because the sampling strategy increasingly ignores individuals who do not exhibit disease symptoms and, so, are far less likely to be tested.
Here, the assumption is that the correlation is always positive. But a negative correlation is also plausible if, say, many symptoms are shared between the disease being tested for and other common maladies. In this case, testing only symptomatic individuals could induce a prevalence lower than random sampling if, for instance, many individuals infected with the disease in question are asymptomatic.
The main lesson is that a failure to account for potential correlations between a sampling strategy and the quality of estimations arising from data collected by it cannot be alleviated by simply collecting more data in the same way. The Literary Digest learned this lesson the hard way. Two years after its disastrous presidential polling flub, the publication failed and its subscriber list was sold to Time magazine. George Gallup’s name, on the other hand, became synonymous with general polling and the organization he founded continues to bear out his legacy.





